数学分析课程中数学概念教学的探讨

廖春艳 赵艳辉

（湖南科技学院 数学与计算科学系，湖南 永州 425199）

数学分析课程中数学概念教学的探讨

廖春艳 赵艳辉

（湖南科技学院 数学与计算科学系，湖南 永州 425199）

通过具体事例，从概念的引入、概念的内含和概念中所蕴含的数学思想方法等方面对数学分析课程中数学概念的教学进行了探讨。

数学概念；数学分析；数学思想方法；极限

数学概念高度凝结着数学家的思维，是数学地认识事物的思想精华，是数学家智慧的结晶，蕴含了丰富的数学思想方法；数学是思维的体操，因此在概念学习中要注重培养学生的思维方式、方法以及迁移能力。由于数学分析课程概念多，数学思想方法丰富，要想学好数学分析，就要深刻理解每一个数学概念以及概念所蕴含的数学思想方法。因此在数学分析课程的教学中注重数学概念的教学就显得尤为重要。

1 自然、合情合理引入概念

数学以抽象的形式反映着客观世界，但这种抽象来源于客观的现实世界，有着深刻的现实背景，绝不是数学家刻意创造的空中楼阁。数学概念也并不是人为的简单约定，而是和客观世界有着千丝万缕的联系，概念的产生过程一定是自然的、合乎情理的。例如定积分（R—积分）是定义在一个有限区间上对有界函数的积分，当区间不是有限的或在有限区间上函数不是有界的，此时积分还有意义吗？该怎样重新定义这种新的积分呢？因此相对于定积分(正常积分)而言，我们可将此种积分命名为反常积分？由极限定义与定积分定义不难得出反常积分的定义；又如由偏导数的定义不难得出方向导数的概念。

2 从解决问题引入概念

学生对数学概念的认识有一个从字面理解到实质性理解的过程，必须经历应用环节，让概念直接为问题解决服务。“一个好例子胜过一千次说教”[1]。如一致收敛与一致连续的概念是数学分析的难点概念。关键在于对“一致”的理解，单从字面上或定义的数学表达式中学生难以将一致收敛与收敛、一致连续与连续区分开来。如果能辅之以例题则问题就好办多了。

再引出一致收敛的概念，这样学生对点态收敛和一致收敛的区别有了一定的认识。也说明了引入一致收敛概念的必要性。

3 围绕概念的核心展开教学

通过适当的方式引入数学概念以后，还要围绕概念的核心展开教学。极限概念是数学分析中最基本、最重要的概念之一，极限概念中包含了有限与无限的辩证思想，体现了由量变到质变的辩证唯物主义观点，因此加强极限概念的教学，掌握极限思想是学好数学分析的关键。在引进数列极限的ε-N定义之前，可以通过大量的例子来体会“无限趋近”的含义；可以通过对同一数列取不同的ε值来说明N的存在性，使学生理解ε的任意性及确定性，N的不唯一性。从而能够理解为什么在用数列极限的ε-N定义证明

4 充分挖掘概念所蕴含的思维方式

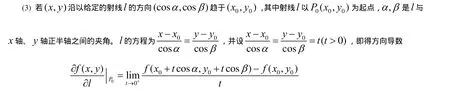
5 理解概念所蕴含的数学思想方法

数学基础知识与数学思想方法是数学教学的两条主线，基础知识是一条明线，而思想方法是一条暗线，隐藏在基础知识的背后，需要深入挖掘并加以提炼。我们要强调数学知识及其蕴含的思想方法教学的重要性，解题训练应针对概念的理解和应用，要让学生养成从基本概念出发思考问题、解决问题的习惯。如定积分概念是整个数学分析中积分学概念的基础，定积分概念中所蕴含的定积分思想（分割、求和、取极限）是定义重积分、线积分、面积分概念的基本思想，对定积分概念的理解直接关系到重积分、线积分、面积分概念的理解。

结束语

课堂中，要加强“从概念出发思考问题”的引导。具体到一堂课，教学中应该突出核心概念、主干知识；应围绕“概念的核心”展开教学；应当教概念的联系与转化。使学生学会根据问题需要调动头脑中的知识，教会学生数学地看待问题、思考问题和解决问题的方法。

[1]章建跃,陶维林.概念教学必须体现概念的形成过程[J].数学通报,2010,(1):25-30.

[2]华东师范大学数学系.数学分析(上册)[M].北京:高等教育出版社,2001.

[3]陈纪修,於崇华,金路.数学分析(下册)[M].北京:高等教育出版社,2004.

[4]赵艳辉,王湘平.定积分教学中学生数学研究能力的培养[J].湘潭大学学报,2010, (12):92-94.

G633.6

A

1673-2219（2014）05-0004-03

2013－05－10

湖南省教改课题（课题号[2012]401号，No.428。）

廖春艳（1984－），女，江西人，硕士，讲师，主要从事微分几何与数学分析的教学研究。

（责任编校：刘志壮）