大破口LOCA事故ASTRUM最佳估算分析方法优化研究

余建辉 张经瑜 郑利民

大破口LOCA事故ASTRUM最佳估算分析方法优化研究

余建辉 张经瑜 郑利民

（上海核工程研究设计院 上海 200233）

ASTRUM (Automated Statistical Treatment of Uncertainty Method)分析方法是美国西屋公司开发的能够自动执行不确定性计算的最佳估算方法。在该方法中，对于部分对大破口LOCA (Loss of Coolant Accident)事故计算结果具有重要影响的参数，采用了参数保守性确认分析的办法，以确定其保守的取值组合。然后，在此基础上执行对其它参数抽样的ASTRUM最佳估算。这种做法对于不同的事故工况或抽样工况得到的保守性参数取值组合可能不同，具有一定的偶然性，在固定这些参数保守组合的基础上再对其余参数抽样进行最佳估算，可能会导致ASTRUM计算结果出现一定程度的偏差。本文取消了原ASTRUM方法中参数保守性确认分析这一环节，通过开发自编的BE_SAMPLE抽样程序，对原参数保守性确认分析中的重要参数进行抽样，执行了全参数的抽样统计分析，并给出了优化结论，它可以为后续ASTRUM方法的优化和研究提供参考。

大破口失水事故，最佳估算，ASTRUM

核电厂事故安全分析的一个重要目标就是论证核电厂设计能够满足安全要求。然而，核电厂的分析计算因受到科学技术、分析方法和计算工具的限制，可能会存在许多不确定性甚至是盲区。为了确保核电厂安全，在特定条件下，在分析中只能采用保守的处理方法考虑参数不确定性的包络值。

在1973年，基于当时LOCA (Loss of Coolant Accident)事故分析水平，美国核管会(US NRC)发布了10CFR50附录K，它规定了LOCA事故分析方法、主要假设和验收准则。随后，在很长的一段时间内，为满足这一准则的要求，核工业界均采用保守的计算模型进行LOCA事故分析。在这种情况下，由于分析的假设条件和计算模型过于保守，使得核电厂LOCA事故分析结果过于保守，由此降低了核电厂的经济性。

随着LOCA事故分析技术水平和计算工具性能的不断提升，事故分析的计算模型更加精细，它对物理现象的分析更加准确，人们可以逐渐减少以往分析中参数不确定性的过度的保守假设，在事故分析中更多地开发和应用最佳估算分析方法。在1988年9 月，美国NRC修订了10CFR50.46(a)(1)(i)，允许采用现实的事故分析方法，但是，它同时严格规定这种方法必须考虑数据和计算模型的不确定性。

ASTRUM (Automated Statistical Treatment of Uncertainty Method)分析方法是美国西屋公司开发的能够自动执行不确定性计算的最佳估算方法，该方法当前主要应用于大破口LOCA事故最佳估算分析，在2004年11月它已经通过US NRC认证。与其它最佳估算方法一样，ASTRUM方法能够较真实地反映核电厂事故瞬态物理过程，并计算满足特定的置信度和概率要求的最佳估算结果。此外，由于该方法能够执行自动统计计算，在较大程度上简化了计算流程，提高了计算效率[1–2]。

然而，当前用于大破口LOCA事故分析的ASTRUM最佳估算方法与标准的最佳估算方法之间仍存在一定差距。在分析中它考虑了部分重要参数的保守性，在ASTRUM方法中有一个重要的计算步骤是参数保守性确认分析，目的是确定某几个重要参数的保守性组合，随后再进行其余重要参数不确定性的抽样统计，进行最佳估算分析。因此，当前大破口LOCA事故ASTRUM分析方法并未对全部的重要参数进行最佳估算，它是基于考虑部分参数保守性的最佳估算方法。

本文针对当前的ASTRUM分析方法，对其重要参数抽样方式及分析步骤进行优化探讨，为后续对ASTRUM方法的改进提供参考。

1 ASTRUM分析方法简介

为了统计大破口LOCA事故瞬态过程中各个重要输入参数及其不确定性对大破口LOCA事故分析结果的影响，ASTRUM方法采用抽样统计(Order Statistics)的数学方法，计算满足特定的概率和置信度要求的计算结果。在抽样统计方法中，对于单个输出参数，可由Wilks经验关系式[3]计算抽样统计次数(N)：

式中，β为置信度；γ为概率；N为次数。

对于计算满足具有95%置信度和95%概率的要求的单个输出参数，应用Willks关系式预测需要进行59次的参数不确定性抽样统计，计算的参数最大值即可满足具有两个95%的置信度和概率的要求。

若某一统计过程涉及多个输出参数，计算多个输出参数满足特定的置信度和概率的要求，可由式(2)计算N：

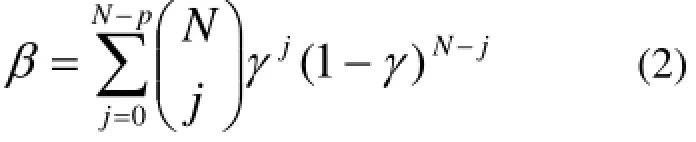
式中，p为需要满足特定置信度和概率要求的输出变量数目。

在应用ASTRUM方法进行大破口LOCA事故最佳估算分析中，需要确定满足具有两个95%置信度和概率的要求的输出参数共有3个，即：燃料包壳峰值温度(Peak Cladding Temperature, PCT)、燃料包壳局部最大氧化量(Local Maximum Oxidation, LMO)和全堆芯总的氧化量(Core Wide Oxidation, CWO)。将p=3代入式(2)，可以计算出N为124次。因此，在应用ASTRUM方法分析中共需要对相关计算输入参数进行124次采样，确定124个计算工况，每个输出参数的最大值可满足具有两个95%置信度和概率的要求。

根据美国NRC早期认可的最佳估算方法论CSAU (Code Scaling, Applicability and Uncertainty)，必须识别瞬态过程的重要现象，筛选出对计算结果具有重要影响的参数，确定其不确定性分布区间和概率分布函数，并综合分析这些重要参数的不确定性传播，从而确定输出参数计算结果的不确定性[4]。

ASTRUM方法对影响大破口LOCA事故的大部分重要参数的不确定性进行统计，同时，它对部分重要参数则进行保守处理，采用其保守的参数组合（如：蒸汽发生器传热管堵管份额(Steam Generator Tube Plugging, SGTP)、厂外电源的可用性(Out Power Available, OPA)、外围低功率组件占堆芯总的功率份额(Rod Relative Power in Low Power Region, RODPLOW)等参数）。在ASTRUM方法中，它称之为参数保守性确认分析(Confirmatory Study)。

2 参数保守性确认分析的局限性

参数保守性确认分析的目的是确定未纳入程序自动抽样范围的多个重要特征参数的保守取值组合。在现有ASTRUM分析方法中，分别考虑这些参数的最大或最小值，组成不同的组合并进行敏感性分析，选择可导致 PCT最高的取值组合作为保守的参数组合。通常这些参数对结果的保守方向不确定或不易判断，否则，对于已知其保守方向的参数直接取其保守方向的值即可，而无需进行组合敏感性分析。因此，这些参数不同的最大或最小值取值组合均可能导致较高的PCT结果。参数保守性分析在确定最保守的取值组合后为后续执行ASTRUM最佳估算做准备。

实际计算过程中，对于不同的事故工况，出现最高PCT结果的取值组合的确可能不同。例如OPA，厂外电源是否有效意味着主泵在破口发生前期是有动力按额定转速运转还是无动力在破口流量作用下超速，在破口喷放前期由于主泵侧破口流量极大，主泵按额定转速运转会阻碍冷却剂通过破口流失，而在破口喷放后期，主泵按额定转速运转则会使得更多的冷却剂通过破口流出。因此，厂外电是否有效在破口喷放的不同阶段对PCT影响的保守方向呈竞争关系。因此，对于具体的破口工况，可能是厂外电有效导致高的PCT，也可能是厂外电无效导致高的PCT。本文将以某个原型核电厂为例，开展参数保守性确认分析及后续的ASTRUM最佳估算。

现有的ASTRUM方法中需要确定保守性组合的重要参数SGTP、OPA、RODPLOW的取值如下：

(1) SGTP：最大值10%，最小值0%；

(2) OPA：厂外电源有效 1，厂外电源无效 0；

(3) RODPLOW：最大值0.8，最小值0.2。

因此，这3个参数的不同的参数组合共有23=8个，具体组合对应的工况如表1所示。

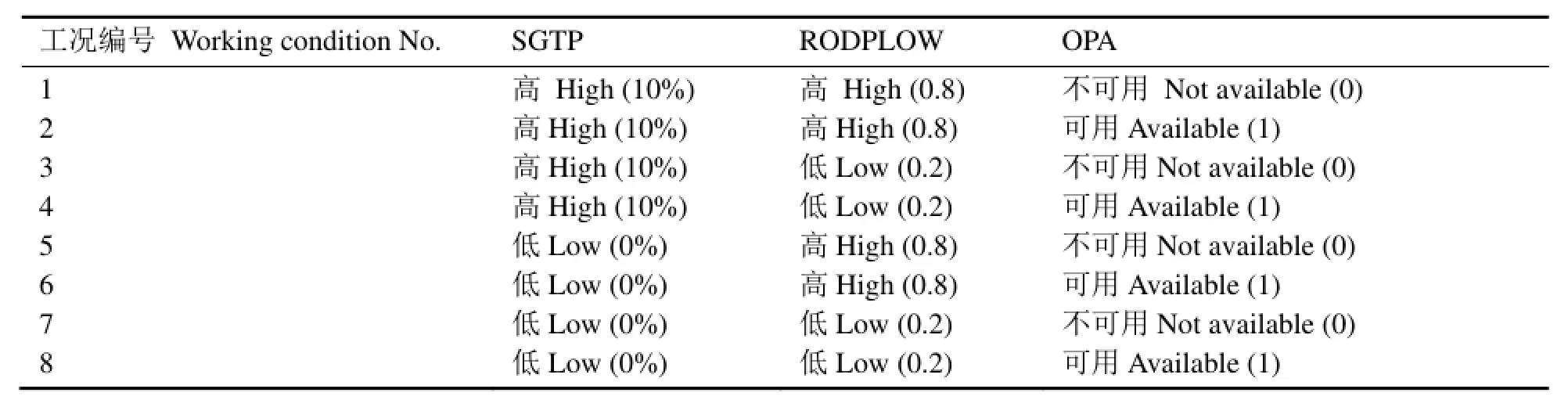
表1 计算工况参数组合说明表Table 1 Definition of analysis case matrix.

在执行参数保守性确认分析中，这8个工况的其余参数完全相同，计算结果如表2所示。

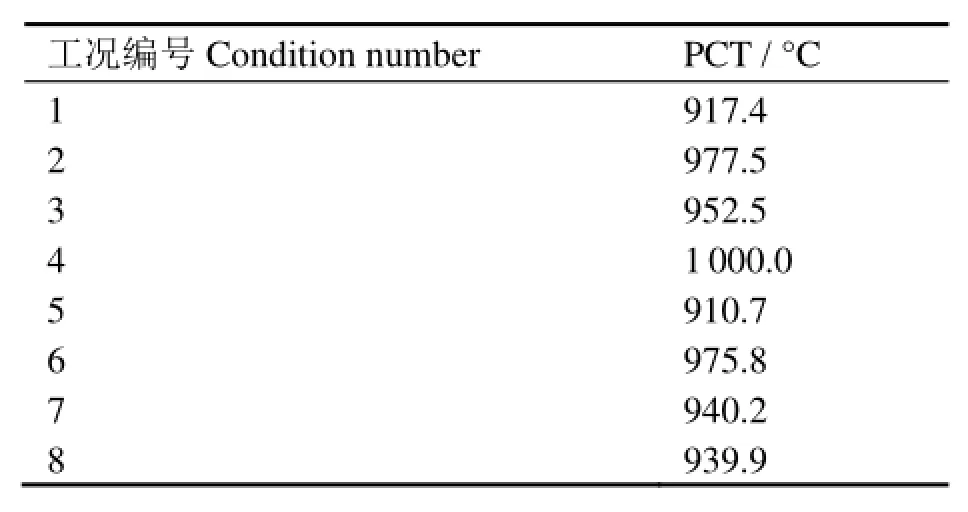
表2 计算工况的8个PCT计算结果对比Table 2 Analysis results comparison.

通过8个工况的计算结果比较，可知第4个工况PCT最高。因此，核电厂包络的参数组合为厂外电有效(OPA，1)、高的蒸汽发生器堵管份额(SGTP，10%)和低的外围燃料组件功率因子(RODPLOW，0.2)，该参数组合将作为参考工况进行下一步ASTRUM不确定性分析。

在应用ASTRUM方法计算中，将按照保守性组合的搭配固定这3个参数值，其余重要参数由抽样程序根据其不确定性分布区间和概率分布函数进行124次抽样，确定124组计算输入参数，并与这3个参数一起由程序自动填入输入文件的对应位置，建立124个工况的程序输入数据文件。最后再分别自动执行计算，确定124个计算工况的输出参数的分析结果。其中 PCT按照由高到低排序的前10名的计算工况分析结果详见表3。因此，核电厂大破口LOCA事故应用ASTRUM方法计算的满足具有两个95%置信度和概率的要求的PCT分析结果为1 054.48 ºC。

根据应用ASTRUM方法的计算流程，可以看出参数保守性确认分析工况是应用ASTRUM方法进行计算分析的基础，在所有的124个计算工况中，构成参数保守性组合的3个参数值都是相同的，其中任一参数的改变可能会影响124个计算工况的分析结果。而对于这3个参数，每个参数只有最大或最小两个取值，它与核电厂的实际情况不符。核电厂真实情况是，在发生大破口LOCA事故时这3个参数可能是在其变化范围内的任意值，仅出现最大或最小值的概率是非常小的。

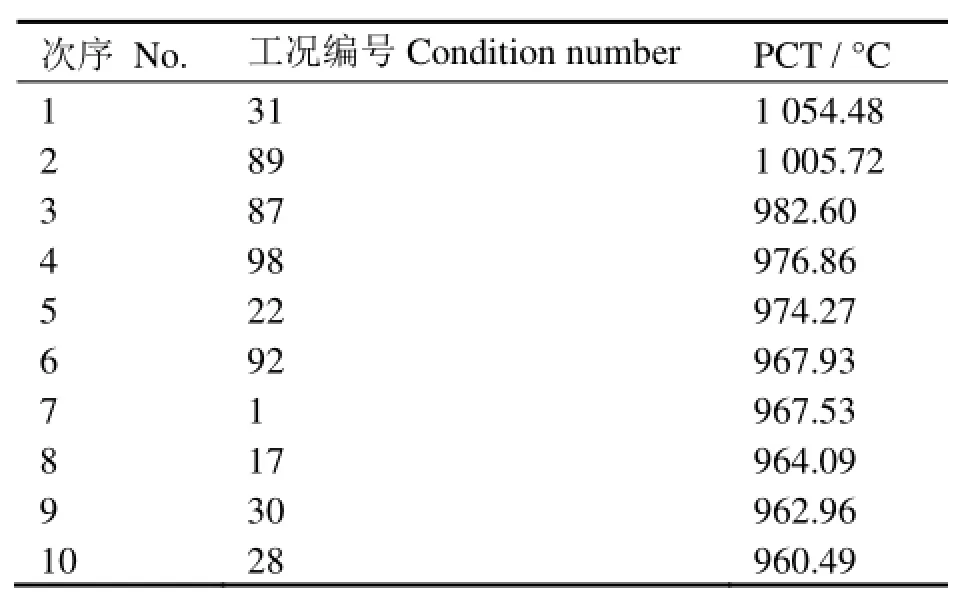
表3 ASTRUM分析得到的PCT前10名工况Table 3 PCT for the first 10 cases.

由表2可见，参数保守性组合敏感性分析结果差异并不大，最高值与次高值差别仅为23.5 ºC，两者相差仅为2.35%。如此小的差值很可能可由程序计算的不确定性所覆盖，从而无法准确地找到其真实的保守组合。而一旦发生误判，将会直接影响整个应用ASTRUM方法的124次计算结果，从而影响计算结果的准确性。

3 全参数抽样统计分析

参数保守性确认分析是ASTRUM固化的程序和历史客观原因的产物，ASTRUM程序包已经封装并固化可以抽样的参数。为了实现全参数范围抽样统计分析，本分析开发了自编的BE_SAMPLE抽样程序，并应用该程序针对SGTP、OPA、RODPLOW进行抽样计算。

通常蒸汽发生器堵管是由传热管损坏造成，若不考虑制造等方面造成的偏差，假定传热管损坏导致的SGTP呈正态分布，分布区间取原ASTRUM计算相同的区间[0%, 10%]；RODPLOW通常由燃耗和装料方案决定，假定事故发生前电厂装换料稳定，RODPLOW为正态分布，分布区间与原ASTRUM计算相同为[0.2, 0.8]。另外，假定事故发生时对电网的扰动造成厂外电有效的概率为50%，厂外电有效服从[0, 1]分布。SGTP、OPA和RODPLOW的分布区间和概率分布函数如表4所示。根据表4，应用BE_SAMPLE程序进行抽样计算，确定124组(SGTP、OPA、RODPLOW)参数，计算结果如图1所示。

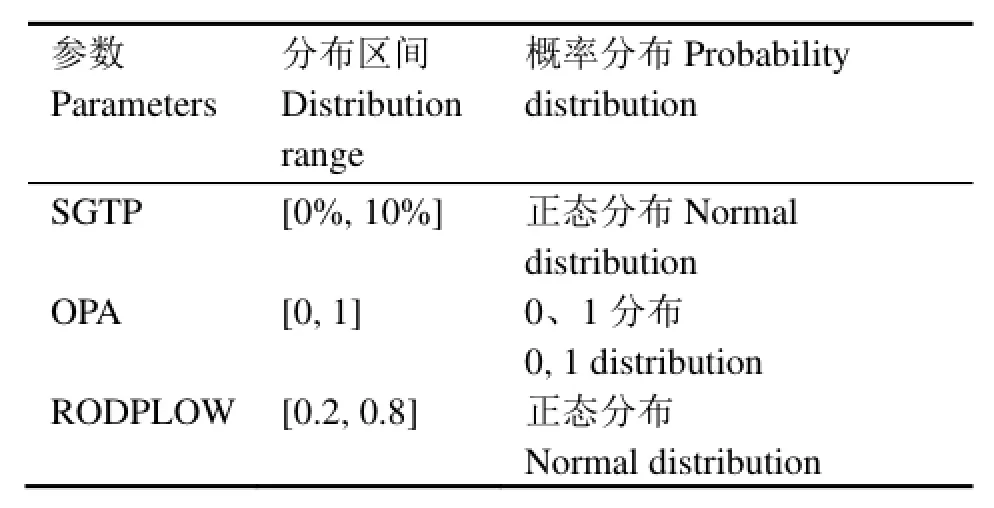
表4 分布区间和概率分布函数Table 4 Distribution and range parameters.

图1 SGTP (a)、OPA (b)、RODPLOW (c)抽样计算结果Fig.1 SGTP (a), OPA (b), RODPLOW (c) sampling results of computation.

在原ASTRUM计算分析中，共有38个重要参数参与了抽样，包括RCS温度、压力、安注箱管线阻力等。本文分析中，仍采用其相同的分布区间和分布函数进行抽样，并同时考虑图1的抽样计算结果，重新确定124组全参数的抽样的计算工况。对每个工况执行大破口LOCA事故计算分析，确定PCT排名前10名的计算工况，其BE_SAMPLE程序抽样工况与大破口LOCA事故PCT计算结果详见表5。

由表5可知，全参数抽样ASTRUM大破口LOCA事故分析计算的满足具有两个95%置信度和概率的要求的PCT为1 045.90 ºC，它比原ASTRUM计算结果低8.58 ºC。在这10个计算工况中，考虑全参数抽样后的计算结果与原计算结果相比，PCT有高有低，其中使PCT升高的计算工况有4个，使PCT降低的计算工况有6个，它再次说明OPA、SGTP及RODPLOW这三个参数对PCT计算结果的保守性影响具有一定的不确定性，若依据三个参数最大或最小值的保守组合的敏感性分析结果来确定参数的保守组合，这种做法将会使分析结果具有一定的偶然性。

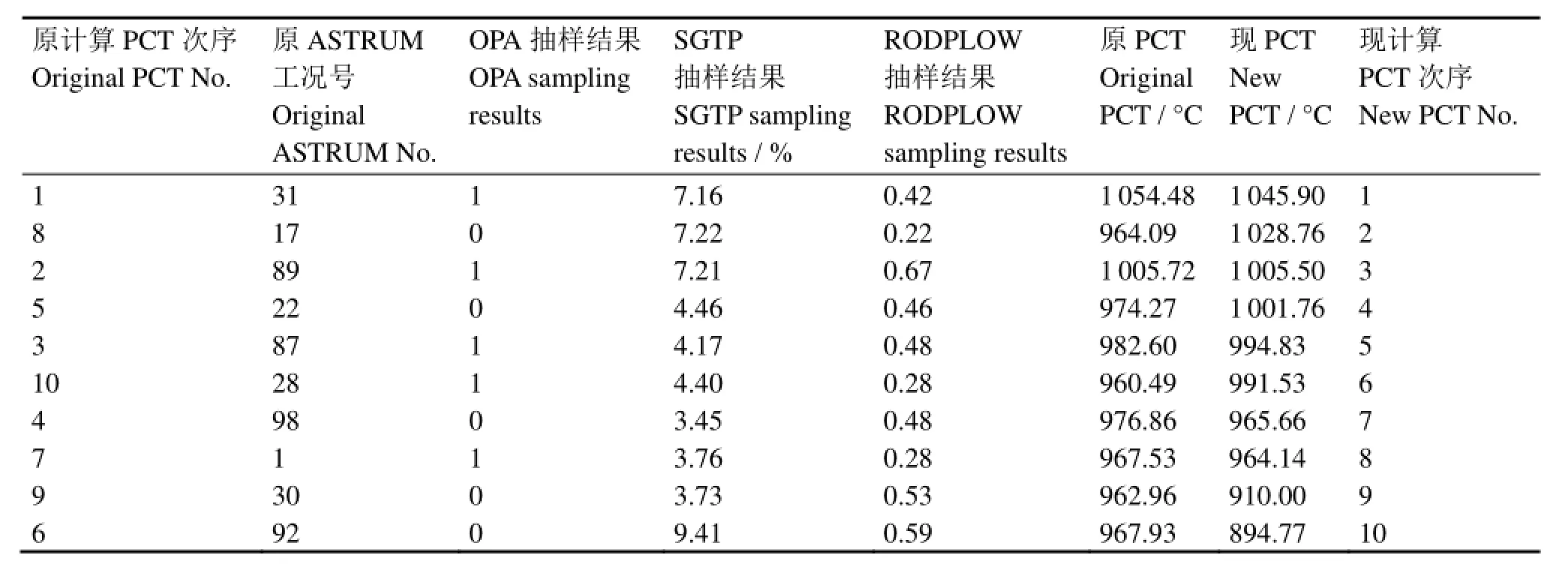
表5 全参数抽样ASTRUM计算结果Table 5 ASTRUM analysis results for a complete set of parameters.

4 结语

简要介绍了ASTRUM方法的原理和一般处理过程，针对其中部分重要参数未纳入最佳估算统计而采用参数保守性确认分析的处理办法，展开优化探索，通过开发和应用自编的BE_SAMPLE程序，对这部分重要参数进行抽样计算，将ASTRUM分析方法拓展为全参数抽样统计。分析结果表明，在分析方法优化后，计算的PCT分析结果有所降低，在一定程度上增大了大破口LOCA事故分析的裕量；同时，由于无需采用参数保守性确认分析，它可消除由参数保守性确认分析可能引起的参数值计算的不稳定，以及因无法准确判断保守参数组合而引入的风险，优化分析方法在简化计算流程的同时，它使计算结果更加可靠。

1 Frepoli C. An overview of Westinghouse realistic large break LOCA evaluation model[J]. Science and Technology of Nuclear Installations, 2008: 498737

2 Frepoli C, Ohkawa K, Kemper R M. Realistic large break LOCA analysis of AP1000 with ASTRUM[C]. Proceedings of the 6thInternational Conference on Nuclear Thermal-Hydraulics, Operations and Safety (NUTHOS ’04), Nara, Japan, October 2004

3 Wilks S S. Determination of sample sizes for setting tolerance limits[J]. The Annals of Mathematical Statistics, 1941, 12(1): 91–96

4 USNRC. Regulatory guide 1.157 (task RS 701-4), best estimate calculations of emergency core cooling system performance[R]. US Nuclear Regulatory Commission, 1989

CLCTL364

Study on ASTRUM optimization for large break LOCA analysis

YU Jianhui ZHANG Jingyu ZHENG Limin
(Shanghai Nuclear Engineering Research & Design Institute, Shanghai 200233, China)

Background:The ASTRUM (Automated Statistical Treatment of Uncertainty Method) methodology is developed by Westinghouse. In this method, some important parameters for large break loss of coolant accident (LBLOCA) analysis are treated conservatively to get a conservative set, which is called confirmatory study. And the value set of parameters is then used to generate the reference transient input deck of ASTRUM calculation. The value set may be varied in different sampling cases. However, the ASTRUM is executed based on one value set of some parameters, although other parameters are sampled. The result of the ASTRUM calculation may be not very exact.Purpose:The aim of this study is to reduce the uncertainty and conservatism, and optimize the ASTRUM.Methods:The parameters concerned in the confirmatory study of ASTRUM were sampled by BE_SAMPLE code developed by this paper for each ASTRUM case. The optimized ASTRUM is executed in company with other sampled parameters.Results:The results of the original and optimized ASTRUM calculations are compared, and the peak cladding temperature (PCT) calculated by new ASTRUM is lower than the original result.Conclusion:The study on ASTRUM optimization reduces the uncertainty caused by confirmatory study, which makes the ASTRUM calculation much more precise.

Large break loss of coolant accident (LBLOCA), Best estimate (BE), ASTRUM (Automated Statistical TReatment of Uncertainty Method)

TL364

10.11889/j.0253-3219.2014.hjs.37.090606

余建辉，男，1982年出生，2006年于清华大学核科学与技术专业获硕士学位，现主要从事反应堆热工安全分析

2014-04-30，

2014-06-15