传感器布置对水轮机振动特征参数影响研究
李瑞莹,李志华
(河海大学 能源与电气学院,江苏 南京 211100)
振动是反映水轮机健康状况及运行安全的重要指标。随着科学技术的进步,一方面水轮机容量、比速和调节的越来越频繁,使得对水轮机振动及运行安全的要求愈来愈高;另一方面,随着传感器技术的发展,振动检测与分析的水平也在不断上升。因而采用好的振动检测方法,提高故障诊断及处理水平,将振动控制在合格范围内,对水轮机正常运行有十分重要的意义。
文中从数学建模及仿真的角度研究传感器布置对水轮机振动特征参数的影响,在传统三点检测法的基础上,同时建立二点和四点法的主轴旋转数学模型,以扫描点处的相对误差为特征参数进行研究。第一、二、三节分别分析了3种传感器布置方法对特征参数的影响,通过对仿真结果的比较得到最佳的传感器布置方法。
1 三点布置法传感器位置对振动参数影响
1.1 三点法主轴旋转数学模型的建立
传统的旋转误差三点法检测原理图如图1所示。

图1 三点法检测原理图Fig. 1 Detection principle diagram of three-point method
图中,A,B,C为三个非接触式涡流传感器。O点为这3个测点的理想旋转中心,以O点建立直角XOY坐标系,同时设∠AOB=α,∠BOC=β。取主轴系统的瞬时旋转轴中心O为极心作极坐标系,极角θ为逆时针方向, R(θ)为主轴旋转误差,在极坐标中它可以分解为Rx(θ),Ry(θ)。r(θ)是极坐标下θ角对应的主轴半径。这样整个主轴的运动就可以用主轴瞬时旋转中心在直角坐标系中的旋转误差和主轴本身在极坐标系中的转动[1]来描绘。
参考三点法检测原理,建立三点法主轴旋转模型[2]图如图2所示。

图2 三点法主轴旋转数学模型Fig. 2 Spindle rotation mathematical model of three-point method
如图,已知主轴标准圆方程为x2+y2=r2,圆上任意一点的直角坐标为(x,y),极坐标为(ρ,θ),经过倾斜角δ,圆心平移到(x0,y0)后,图形上任意一点的直角坐标变为(x1,y1),新的旋转平移方程可推导如下:
1)逆时针倾斜角,图形上任意一点的极坐标值由(ρ,θ)转化为 (ρ,θ+δ)

3)将解带入标准圆方程,变形为

4)将三个传感器与标准圆心所在直线看成三条扫描线,且设直线方程为y=kx,联立该直线与上式可简化为一个一元二次标准方程ax2+bx+c=0,其中

1.2 传感器位置对振动参数影响
仿真时,设主轴旋转的标准圆方程为x2+y2=402,以3个传感器夹角α=120°,β=120°为标准情况来进行布置,此时扫描直线斜率k1=0,k2=-1.732 1,k3=1.732 1[3]。在MATLAB中仿真编程,可得到S1、S2、S3在相对扫描点处的测量数据(X1,Y1)、(X2,Y2)、(X3,Y3)。同时由于每个传感器沿X和Y 方向的分量都有自己独特的频率成分,首先对测量数据进行FFT变换,将时域信号转化为频域信号[4],进一步进行观察。得到三点布置法中FFT波形图如图3所示。
对FFT波形图进行分析,可知频率对旋转误差几乎没影响,但振幅对旋转误差的影响却很大,接下来只考虑振幅,忽略频率对旋转误差的影响。
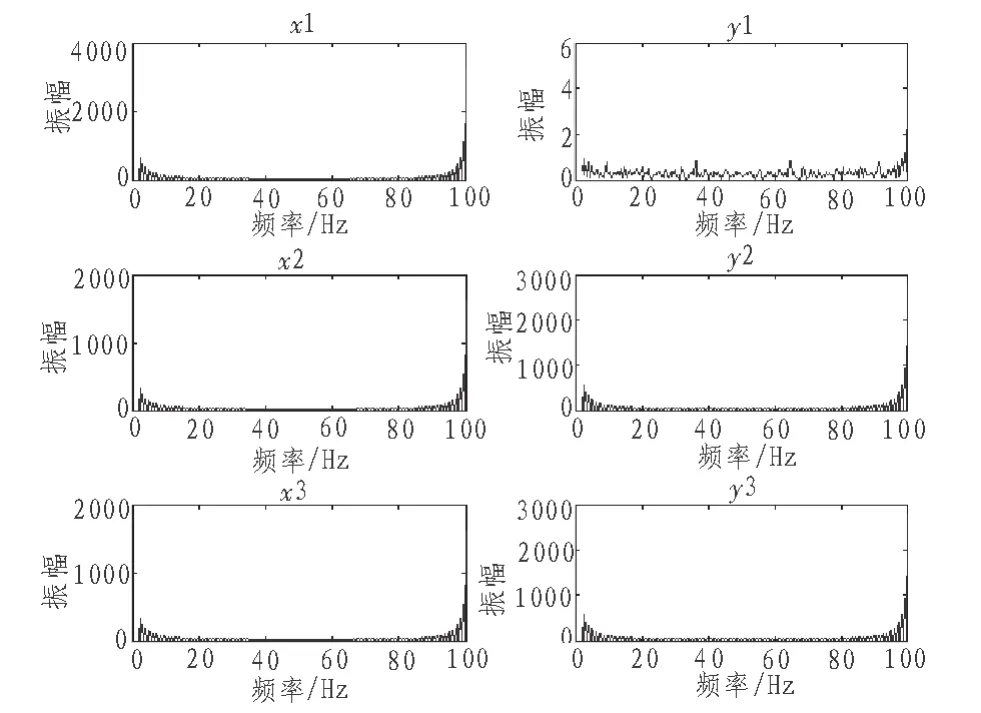
图3 三点法FFT波形图Fig. 3 FFT waveform of three-point method
当只α变化β不变时,以α=120°,β=120°为标准情况用“0”表示[5];α每减小2°代表负偏离一个单位度,用“-1”表示;α每增加2°代表正偏离一个单位度,用“1”表示。由于α和β的变化只影响(X2,Y2)和(X3,Y3)的测量值,故以(X2,Y2)和(X3,Y3)为被测对象,同时以最大相对误差值作为特征参数进行研究,经过MATLAB仿真,得到特征参数与角度的关系曲线如图4所示。

图4 三点法仅α变化时最大相对误差曲线Fig. 4 Maximum relative error curve of three-point method only α change
观察可知,随α角度变化Y2和Y3最大相对误差值几乎没什么影响,X2最大相对误差随α偏离度地增大明显变小,X3最大相对误差随α偏离度增大明显变大,总体而言,在-2~2的偏离范围内,整体效果较好。
当只β变化α不变时,以α=120°,β=120°为标准情况用“0”表示;β每减小2°代表负偏离一个单位度,用“-1”表示;β每增加2°代表正偏离一个单位度,用“1”表示。由于β的变化只影响(X3,Y3)的测量值,故以(X3,Y3)为被测对象,同时以最大相对误差为特征参数进行研究,经过MATLAB仿真,得到特征参数与角度的关系曲线如图5所示。
观察可知,随β角度变化Y3最大相对误差几乎没什么影响,但整体呈上升趋势,在-10~0的偏离范围内整体效果较好。

图5 三点法仅β变化时最大相对误差曲线Fig. 5 The maximum relative error curve of three-point method only βchange
2 二点布置法传感器位置对振动参数影响
2.1 二点法主轴旋转数学模型的建立
与三点法主轴旋转数学模型类似,将传感器个数减少为两个,如图6所示,便可得到两点法主轴旋转数学模型,S1,S1为两个传感器所在位置。二点法的数学模型分析过程与三点法类似,这里不再重复。

图6 二点法主轴旋转数学模型Fig. 6 Spindle rotation mathematical model of two-point method
2.2 传感器位置对振动参数影响
仿真时,设主轴旋转的标准圆方程为x2+y2=402,以传感器夹角α=90°为标准情况来进行布置,此时扫描直线斜率k1=0,k2=1.6331e+016。在MATLAB中仿真编程,可得到S1、S2在相对扫描点处的测量数据(X1,Y1)、(X2,Y2)。
当α变化时,以α=90°为标准情况用“0”表示,α角度偏离度设置与三点法相同。由于α的变化只影响(X2,Y2)的测量值,而X2在标况下的真值为0,此时相对误差无意义,故只将Y2的最大相对误差作为特征参数进行研究,经过MATLAB仿真,得到特征参数与角度的关系曲线如图7所示。
观察图7可知,随α角度的变化Y2最大相对误差在0.275%到0.325%范围幅度变化较大,在1到10的偏离范围内整体效果较好。
3 四点布置法传感器位置对振动参数影响
3.1 四点法主轴旋转数学模型的建立
与三点法主轴旋转数学模型类似,将传感器个数增加为4个,如图8所示,便可得到四点法主轴旋转数学模型,S1,S2,S3,S4为4个传感器所在位置。四点法的数学模型分析过程与三点法类似,这里不再重复。

图7 二点布置法Y2相对误差曲线Fig. 7 Y2 relative error curve of two-point method
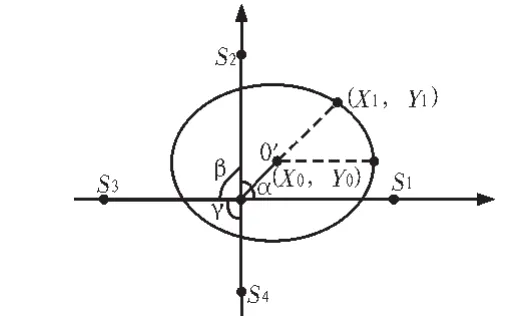
图8 四点法主轴旋转数学模型Fig. 8 Spindle rotation mathematical model of four-point method
3.2 传感器位置对振动参数影响
仿真时,设主轴旋转的标准圆方程为x2+y2=402,以传感器夹角α=90°,β=90°,γ=90°为标准情况来进行布置, 此 时 扫 描 直 线 斜 率 k1=0,k2=1.6331e+016,k3=0,k4=1.6331e+016。在 MATLAB 中仿真编程,可得到S1,S2,S3,S4在相对扫描点处的测量数据(X1,Y1)、(X2,Y2)、(X3,Y3)、(X4,Y4)。
当只α变化,β、γ不变时,以α=90°,β=90°,γ=90°为标准情况用“0”表示;α角度偏离度设置与三点法相同。由于的α变化只影响(X2,Y2)、(X3,Y3)和(X4,Y4)的测量值,且在标况下,X2、Y3和X4的真值为0,此时相对误差无意义,故只研究Y2、X3和Y4在变化时的相对误差值,经过MATLAB仿真得到特征参数与角度的关系曲线如图9。
由图9可知,当α变化时Y2、X3和Y4三者的变化幅度都较大,Y2在偏离度为“1”时取得极小值,在-3~8的偏离范围内效果较好;X3在“-9”处取得极小值,在-10~3的偏离范围内效果较好;Y4在“6”处取得极小值,在0到7的偏离范围内影响较小。总体而言,在0~3的偏离范围内取得较好的效果。
当只β变化,α、γ不变时,只影响(X3,Y3)和(X4,Y4)的测量值,且在标况下,Y3和X4的真值为0,此时相对误差无意义,故只研究X3和X4在β变化时的相对误差值,经过MATLAB仿真,得到特征参数与角度的关系曲线如图10所示。
分析图10可知,随变化,和的变化幅度在0.26%到0.32%的范围内都较大。比较之下,在-2到7的偏离范围内最大相对误差较小;在-2到5的偏离范围内受影响较小。总体而言,在-2到5的偏离范围内效果较好。

图9 四点法仅α变化时最大相对误差曲线Fig. 9 Maximum relative error curve of four-point method only change α
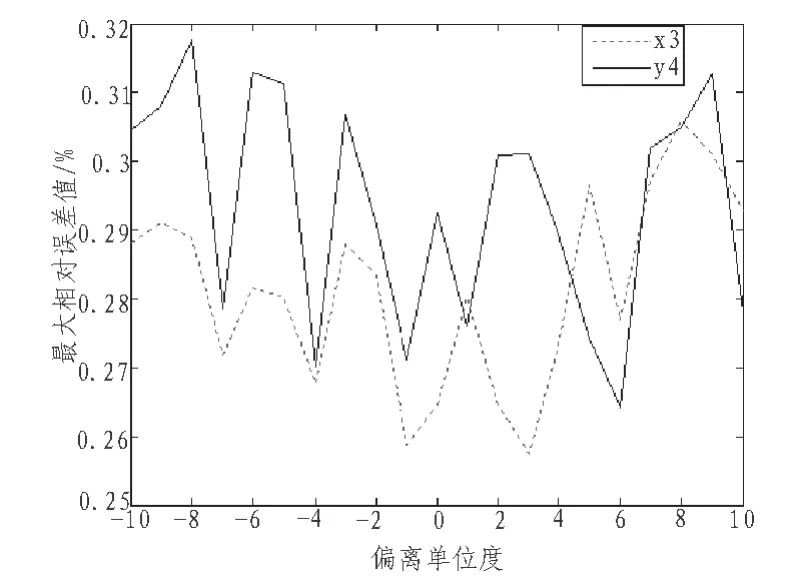
图10 四点法仅β变化时最大相对误差曲线Fig. 10 Maximum relative error curve of four-point method only βchange
当只γ变化,α、β不变时,只影响到(X4,Y4)的测量值,又在标况下,X4的真值为0,此时相对误差无意义,故只研究Y4在γ变化时的相对误差值,经过MATLAB仿真,得到特征参数与角度的关系曲线如图11所示。

图11 四点法仅γ变化时最大相对误差曲线Fig. 10 Maximum relative error curve of four-point method only change γ
由图11可知,最大相对误差值随的变化在0.28%~0.32%的范围内幅值变化大。在标况下取得最小值,且在-1~3的偏离范围内整体效果较好。
3.3 仿真结果分析
将变化时3种传感器布置的最大相对误差曲线图4、图7和图9进行比较,三点法中整体最大相对误差在0.3%~1.4%的区域内变化,且最大值和最小值相差1%;二点法中最大相对误差变化在0.275%~0.325%的区域内,最值之间相差0.05%;四点法中整体最大相对误差在0.254%~0.324%的区域内变化,最大变化范围是0.07%。从曲线变化幅度上看,二点法和四点法的稳定性要优于三点法,且在-7~2的偏离范围内曲线整体效果较好。
同理,将β变化时不同布置方法的最大相对误差曲线图5、图10进行比较,三点法中最大相对误差变化在0.4%~1.4%的区域内,变化幅度为1%;四点法中整体最大相对误差在0.26%~0.318%的区域内变化,变化范围是0.047%。对比可知四点法在曲线变化幅度和最值方面都要优于三点法,且在-2~5的偏离范围内曲线整体效果较好。将变化时的最大误差曲线图11进行分析,此时四点布置法在标况下取得最小值,且在-1~3的偏离范围内整体效果较好。
4 结束语
文中以扫描点处的相对误差值作为振动特征参数,从数学建模和仿真角度研究了传感器布置对特征参数的影响。通过以上分析可知[6],四点布置法的整体效果要优于二点法和三点法,且传感器角度在-1~2的偏离范围内,即α、β和γ布置在88°~94°的范围内整体效果较好。
[1] 沙立华.水轮机发电机振动问题的处理[J].水电厂自动化,2008,29(3):1-2.SHA Li-hua.Turbine generator vibration problem handling [J].Hydropower Automation, 2008,29(3):1-2.
[2] 陈清,梁兵.主轴径向回转误差测量中的误差分析[J].湖南大学学报,2003,30(4):23-25.CHEN Qing,LING Bing. The spindle rotation error measurement of the error analysis[J]. Journal of Hunan University,2003,30(4):23-25.
[3] 张宇华,王晓琳.三点法中测头最佳角位置的确定方法[J].光学精密工程,1998,6(5):39-45.ZHANG Yu-hua,WANG Xiao-lin.Three point method of measuring head best Angle position determination method[J].Optical Precision Engineering,1998,6(5):39-45.
[4] 洪迈生,邓宏煌.加试和回转运行误差的时域二点法分离技术[J].中国机械工程,1997,8(2):88-92.HONG Mai-sheng,DENG Hong-huang.Add try tow point method of time domain and rotary operation error separation technique[J].Mechanical Engineering in China,1997,8(2):88-92.
[5] 范裕健,张社民,徐文雄.三测点法检测的机理及数学模型[J].仪器仪表学报,1994,15(2):155-159.FAN Yu-jian, ZHANG She-min, XU Wen-xiong. Three points method to detect the mechanism and mathematical model[J].Journal of Instruments and Meters, 1994,15(2):155-159.
[6] 韦然.无线传感器网络节点的设计与实现[J].电子科技,2012(1):31-35.WEI Ran.Design and implementation of a general node for wireless sensor networks[J].Electronic Science and Technology,2012(1):31-35.

