一种传感器网络融合算法的优化
刘俊材
(电子科技大学 信息中心,四川 成都 610054)
当前,传感器网络作为一个全新的研究领域,在基础理论和工程技术两个层面向科技工作者提出了挑战性研究课题。其中,作为多源信息处理关键技术基础的信息融合理论显得非常重要。分布式检测信息融合对于无线多传感器网络中信号的提取和处理非常有效。
在分布式多传感器融合问题中,如何在衰减的信道中实现最优决策融合是近几年来国际上刚刚兴起的研究热点,Chamberland和Veeravai[1]研究了错误概率对信道性能的不利影响,根据其发表的文献标明,信号衰减会降低通信系统的整体的性能,但是相比较而言,传感器观测的质量对整体错误概率会有更大的影响。他们还研究了信道能量和信道传输率(即信道限制)对通信的影响,得出在传感器观测信号独立且服从标准正太或指数分布的情况下,采用标准二元区间处理将使传感器达到渐进最优结果。在相似的条件下,Jayaweera[2]分析了基于大数量传感器网络的特性,在该条件下网络中传感器观测使用类似瑞利放大处理器来传递而不是使用二元决策器来传递的结果。他证明了即使在能量和传输率都有限制的信道中,把那些不太好的传感器经过组合使用的得到的最终决策也比仅仅依靠少数几个很好的传感器的信息得到的决策要可靠的多,除了能量和信道容量限制之外,无线传感器网络决策系统的性能还依赖很多其他因素,例如:决策融合率、信道错误控制编码、传感器质量等。衰减信道上的二元决策融合问题已经成为低损失、低能量无线传感器网络应用中的特别重要的问题。在诸多的学者中,Varshney[3]也做了许多有意义的研究工作,他用“衰减层”的形式来描述传感器网络并联网络信道衰减问题,并且得到似然比形式的融合率,最优融合率是传感器局部二元决策和信道状态信息的函数。在此基础上,他又推导出3个“次优”融合率,分别叫做:双阶段融合率,极大似然融合率和平均增益融合率。
Varshney的方法简单明了,特别是3个“次优”融合率具有很强的可操作性,然而其局限性是要求每个传感器的局部数据压缩是独立的,这当然要求传感器的观测必须是独立的,这个条件在实际中不一定能被满足。例如:当传感器都观察一个随机参数的变化时,观测就变得不独立了,上述方法不能再使用。
目前的关键问题在于:由于每个无线传感器和融合中心之间通过无线多径信道相联接,每个无线传感器传给融合中心的信息量受到信道容量的严格制约[3]。如何在信道容量有限的前提下,优化子传感器的局部处理算法和融合中心的融合算法显得尤为重要。以往的研究主要集中在以下几个方面:根据子无线传感器的信道状态决定传送给融合中心的信息量[4];利用数学方法开发高效的融合算法[5]。以上研究多数都没有考虑无线传感器网络以及各传感器的信道容量对系统检测性能的影响。
文献[4-5]提出了在无线多径信道的总信道容量受限情况下基于融合中心最小错误概率原则的最优传感器网络模型。针对上述问题,在文献[6-7]提出的系统模型的前提下,讨论了总信道容量受限的无线传感器网络的融合算法。
1 网络模型
基于融合中心的无线传感器网络系统框图如图1所示。
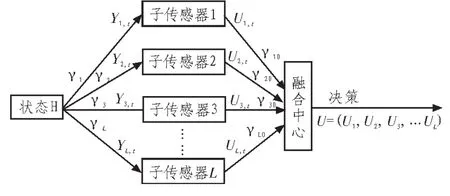
图1 无线传感器网络的系统框图Fig. 1 Wireless sensor network system block diagram
假设无线传感器网络监测关于检测对象A的状态H,其中,H为二进制随机变量,随机地从二进制的信号集{H0,H1}中以概率 P0,P1(P0+P1=1)取值。{γ1,γ2,γ3,…γl}表示检测对象A到各个无线传感器之间的无线信道衰落系数。在系统模型中,假设信道信息在接收端是已知的,即各无线传感器信道的衰落系数已知。由于检测对象 是通过无线信道向各无线传感器传输信息,所以{γ1,γ2,γ3,…γl}是一系列独立同分布并且服从复高斯分布的CN(0,δ2) 随机变量。{Yl,t:l=1,2,…L;t=1,2,…T}(其中L表示传感器数目)表示每个传感器l接收到的关于H的观测值, Yl,t的值可以由式(1)得到:

其中, Zl是高斯白噪声。由式(1)可知: Yl,t是以条件概率为的独立同分布的随机变量,由于无线衰落系数 {γ1,γ2,γ3,…γl}在每个传感器端已知,各传感器根据自身接收到的关于检测对象的数据信息进行二进制检测,并且将判决结果和其判决结果的可信度映射为Ul,t=fl(Yl,t,t),通过无线多径信道传送给融合中心。
2 无线多径接入信道的信道总容量
假设单位面积内无线传感器传输的总功率是定值 P,第l个无线传感器以功率P/L来传送信息Ul,t,当单位面积内的无线传感器数目L很大时,根据大数定理,趋近于随
机变量的方差,根据信息论的基础知识可以计算出无线多径信道的总容量:
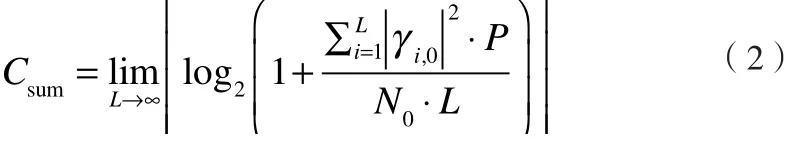
其中, N0是加性白噪声 Z0的方差。根据式(2),可知:趋近于1,所以,无线多径接入信道的总容量为:
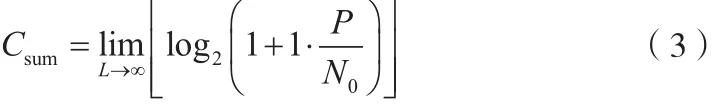
通过式(3)可以得到结论:无线多径信道的信道总容量是个定值,并且定值完全由单位面积无线传感器的发射功率P和加性白噪声的方差所决定。
3 优化后的融合算法
文献[4-5]提出了在无线多径信道的总容量受限情况下,基于融合中心最小错误概率原则的最优传感网络模型。在这个基础上,文中将结合网络信息论的相关知识和信号估计与检测理论中的贝叶斯准则,以尽可能减少系统在融合中心的错误概率为目标来分析和推导融合算法,即尽可能地最小化。根据信息论的基本知识,系统可以保证单位时间内有 Csum比特信息由各无线传感器无误传输至融合中心,假设无线传感器可以在传送关于状态H的判决结果的同时,并且将物体A到各无线传感器之间的无线信道衰落系数{γ1,γ2,γ3,…γL}完整无误的传送至融合中心。基于融合中心最小错误概率原则的最优融合算法推导如下:
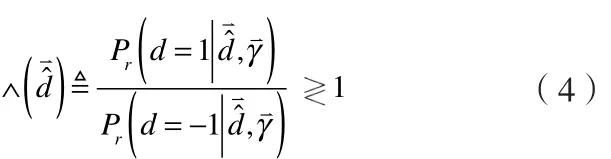
利用贝叶斯准则,不失一般性,假设发射信号是等概率:Pr(d=1)=Pr(d=-1)=1/2,式(4)可以表示为:
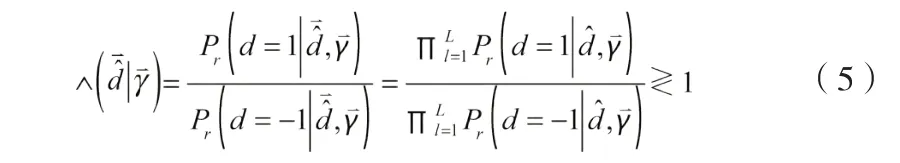
式(5)即为似然函数的比值,设Pl为物体A到第l个传感器之间信道的比特错误概率,那么Pl的值在不同的调制方式下具有不同的解析式。
定两个集合:
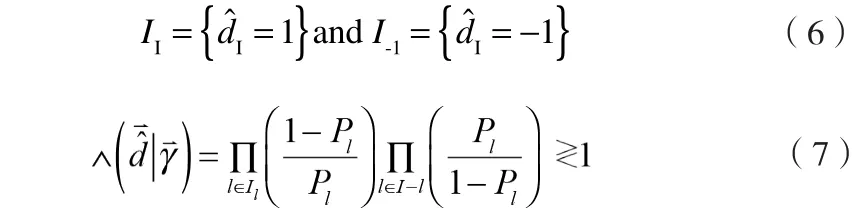
式(7)可以用对数似然函数表示为:
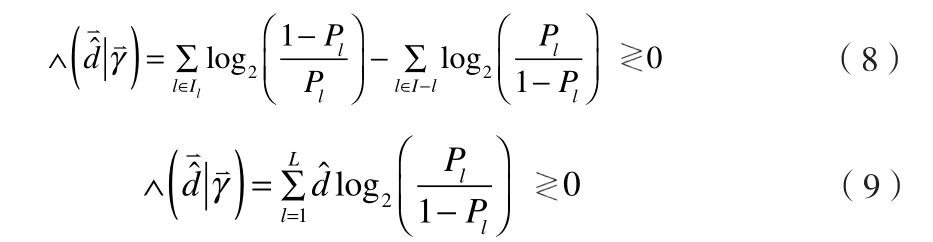
通过式(9)可以发现:在这种情况下,最优的融合算法是对每个无线传感器给融合中心的判决结果进行线性加权,权值l og2(1-Pl)/Pl是各无线传感器判决结果的可信度,取值与Pl有关。
4 结 论
针对无线传感器网络的基于二进制分部检测的问题,当单位面积的无线传感器的数目很大时,系统的总的信道容量趋于定值。在假设无线传感器和融合中心所组成的网络是各向同性并且总信道容量受到制约的情况下,文中提出了融合中心在瑞利慢衰落信道条件下的基于错误概率最小化的最优融合算法以及融合算法的实现方法,弥补了目前研究的模型大多数没有考虑无线传感器网络以及无线传感器的信道容量对系统检测性能的影响的不足。文中提出的融合算法满足在低信噪比区域,具有较低的误码率和复杂度。考虑到无线传感器网络通常用来检测比较微弱的信号源,无线传感器网络对信噪比很小的信源适用,因此,文中提出的融合算法具有很广阔的应用前景。
[1] Chamberland J F,Veeravalli V V.The impact of fading on decentralized detection of power constrained wireless sensor networks[J].IEEE International Conference Proceedings on Acoustics,speech,and Signal Processing (ICASSP04),2004,3:837-840.
[2] Jayaweera S K.Large system performace of constrained decentralized detection with anolog local processing[J].IEEE International Conference on Wireless Network,Commuications and Mobile Computing,2005,2:1083-1088.
[3] Blum R S, Kassam A,Poor H V.Distributed detection with multiple sensor part II:Advanced topics.Proc[J].IEEE,1997,85:64-79.
[4] ZHU Y M.Multisensor Decision and Estimation Fusion[M].Boston,Kluwer Academic Publishers,2003.
[5] Chamberland J F,Veeravalli V V.Asymptotic results fordecentralized detection in power constrained wireless sensor networks.selected areas in communications[J].IEEE Journal on,2004,22(6):1007-1015.
[6] Bogler P L. Sharfer-dempster reasoning with application to mutisenor target identification system[J].IEEE Trans on AES-31,1995,1:9-19.
[7] Chamberland J F,Veeravalli V V.Detection in sensor networks[J].IEEE Transactions on signal processing,2003,51(2):407-416.

