分段多簇压裂水平井产能计算及其分布规律

李龙龙，姚军，李阳,2，吴明录，曾青冬，路然然

（1. 中国石油大学（华东）石油工程学院；2. 中国石化油田勘探开发事业部）

0 引言

分段多簇压裂为一种新的水平井压裂技术，是对套管进行分段多簇射孔，多簇同时压裂，以达到大幅度扩大泄油面积、提高单井产量的目的[1]。水平井分段多簇压裂是低渗透油气藏和非常规油气藏开采的关键技术[2-8]，目前对其产能研究相对较少，主要有数值模拟和电模拟方法：任龙等[1]利用Eclipse软件研究了分段多簇压裂水平井的渗流特征及产能分布规律，杜保健等[9]通过电模拟实验研究了致密油藏分段多簇压裂水平井的压力分布及产能影响因素，但尚无文献报道分段多簇压裂水平井的产能计算公式。本文应用位势理论和叠加原理，考虑裂缝无限导流与有限导流 2种情况，推导分段多簇压裂水平井的产能线性方程组，利用数值分析方法进行求解，得到每簇裂缝的产量及水平井总产量，并通过实例计算分析压裂水平井产能分布及裂缝参数对其影响。

1 分段多簇压裂水平井产能线性方程组

1.1 无限导流裂缝

文献[1，9]均假设分段多簇压裂后的裂缝垂直穿过水平井，据此，本文对水平井分段多簇压裂后的效果作如下假设：共产生N段裂缝，每一段内的裂缝数可任意取值，第i段内共有si簇裂缝，在该段裂缝内，第j簇（1≤j≤si）裂缝的编号为（i，j），裂缝（i，j）到裂缝（i，j+1）的间距为di,j，裂缝（i，si）到裂缝（i+1，1）的距离为li，裂缝（i，j）的半长为Lfi,j。

图1 分段多簇压裂水平井模型

以水平井中点为坐标原点（0，0），水平井中心线为y轴，裂缝（m，n）与水平井交点的坐标为（0，y0m,n），其在（x，y）处的势函数为[10]：

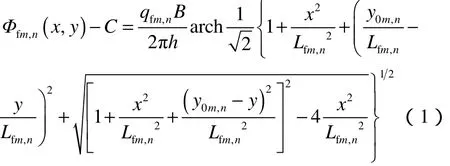
由（1）式可得，裂缝（m，n）在供给边界（0，re）处的势函数为：

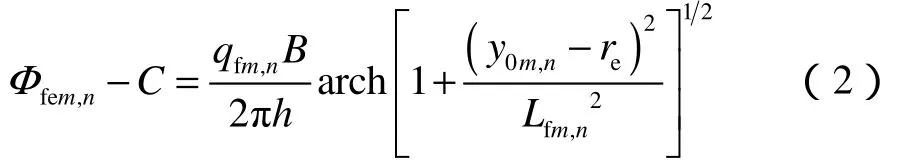
裂缝（m，n）在裂缝（i，j）与水平井交点（0，y0i,j）处的势函数为：

假设裂缝与水平井交点处的压力为井底流压，根据势的叠加原理[11]，将所有裂缝在裂缝（i，j）与水平井交点（0，y0i,j）处造成的势函数相加，可得Φw方程：

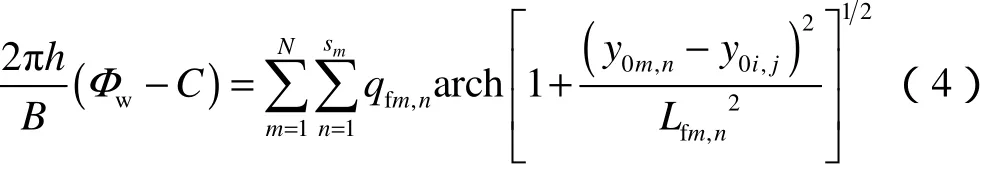
每条裂缝与水平井的交点均对应一个Φw方程，因

将所有裂缝在供给边界（0，re）处造成的势函数相加，可得1个Φe的方程：

已知势函数表达式为 Φ=Kp/μ，（5）式减（4）式整理后可得：

则（6）式可以简化为：

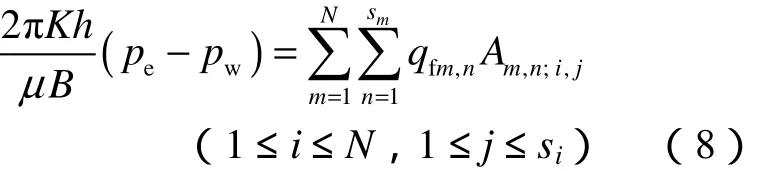
1.2 有限导流裂缝

考虑裂缝内的渗流阻力时，由于裂缝的半长远大于水平井筒的半径，所以裂缝内的流体从裂缝边缘向井筒周围聚集[12]，如果忽略重力的影响，可以将裂缝（i，j）内的流动近似看作某地层的平面径向流，地层厚度为裂缝开度、流动半径为h/2，边界压力为pfi,j，井底压力为pw(裂缝底部的压力)，则下式成立：

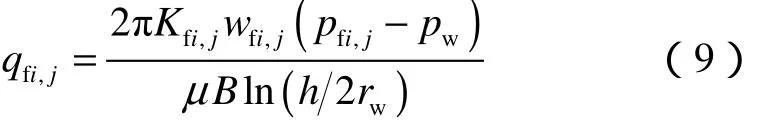
由（9）式可得：

考虑裂缝导流能力之后，（8）式变为：

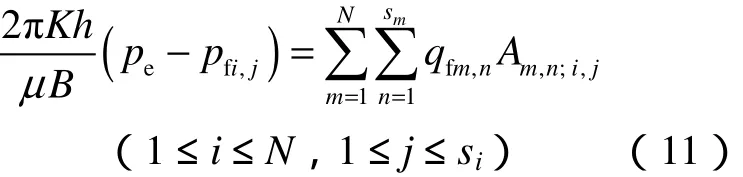
2 实例计算及分析

以某油藏 1口水平井为例，假设不同压裂情况进行产能计算，并对结果进行分析。主要参数为：油藏厚度15 m，供油半径800 m，水平井段长度400 m，井筒半径 10 cm，供给边界压力 30 MPa，井底压力 23 MPa，油藏渗透率0.02 μm2，流体黏度6 mPa·s，体积系数1.2。

2.1 2段5簇裂缝

假设长度为L的水平井存在2段裂缝，第1段有3簇裂缝，裂缝半长分别为 Lf1,1、Lf1,2、Lf1,3，裂缝间距分别为d1,1和d1,2，第2段有2簇裂缝，裂缝长度分别为 Lf2,1、Lf2,2，裂缝间距为 d2,1，2段裂缝间的距离为l1=L−（d1,1+d1,2+d2,1）。

2.1.1 无限导流裂缝

根据（8）式可得压裂2段5簇裂缝时无限导流裂缝的产能线性方程组：

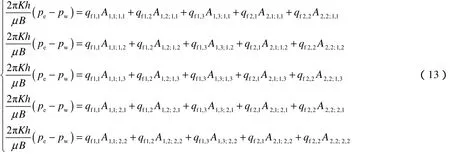
实际裂缝参数为：d1,1=30 m，d1,2=40 m，d2,1=30 m，l1= 300 m，假设4种裂缝半长方案（见表1）进行计算。将以上参数代入（13）式，利用数值分析方法求解，可得每一簇裂缝的产量，求和得到总产量。

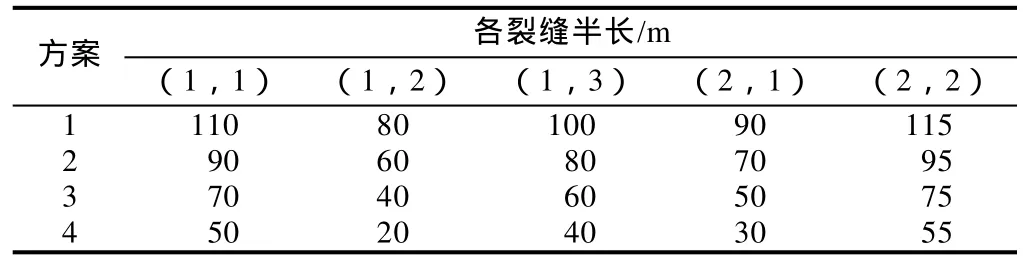
表1 2段5簇压裂水平井的裂缝半长

由图2和图3可知：①对于第1段的3簇裂缝，外侧裂缝（1，1）对总产量的贡献最高，其次为内侧裂缝（1，3），最后为中间裂缝（1，2），说明每段有2簇裂缝即可保证较高产量，超过 2簇时应优先增大外侧与内侧裂缝的半长；②对于第2段的2簇裂缝，外侧裂缝（2，2）对总产量的贡献比内侧裂缝（2，1）高；③水平井两端的外侧裂缝（1，1）和（2，2）的产量对裂缝半长均非常敏感；④总产量随所有裂缝半长的减小下降明显；⑤压裂设计时，应尽量增大裂缝半长，重点是水平井两端的外侧裂缝。

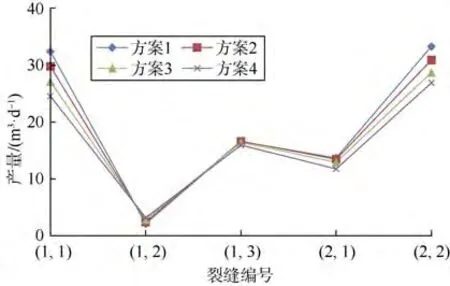
图2 2段5簇压裂水平井每条裂缝的产量

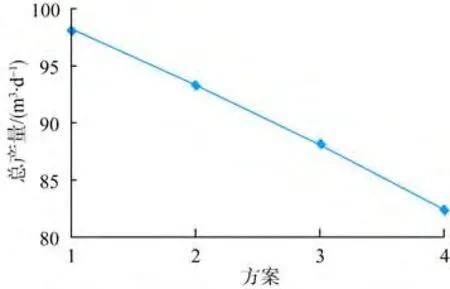
图3 2段5簇压裂水平井总产量

2.1.2 有限导流裂缝

根据（12）式可得压裂2段5簇裂缝时有限导流裂缝的产能线性方程组：

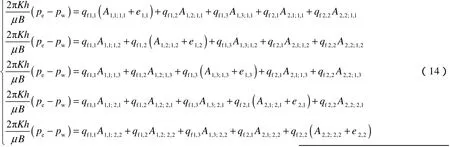
实际裂缝参数为：d1,1=30 m，d1,2=40 m，d2,1=30 m，l1=300 m，各裂缝半长均为100 m。将以上参数代入(14)式，利用数值分析方法进行求解，可得不同导流能力条件下每簇裂缝的产量，进而得到总产量，结果见图4、图5。

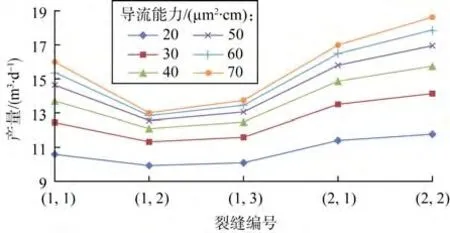
图4 2段5簇压裂水平井不同导流能力时每条裂缝的产量

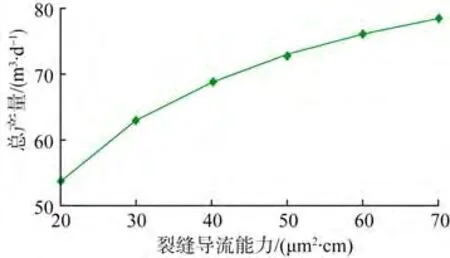
图5 2段5簇压裂水平井总产量随导流能力的变化

由图4和图5可知：①相对无限导流裂缝，裂缝有限导流时产量分布发生变化，同一段内裂缝间的产量差距减小，尤其是裂缝（1，2）对总产量的贡献增大明显，而水平井两端的外侧裂缝对总产量贡献减小，但产量分布的总体规律与裂缝无限导流时相同；②裂缝导流能力对产能的影响比较大，但两者之间并非线性关系，随着裂缝导流能力的增大，产量增加的幅度逐渐减小，根据不同裂缝导流能力所对应的压裂成本，可以确定最佳的裂缝导流能力。

根据无限与有限导流裂缝两种情况下的产能计算结果，在分段多簇压裂设计时，每段 2簇裂缝即可保证较高产量，与文献[9]的电模拟结果相同。

2.2 压裂段数对产能的影响

假设压裂段均匀分布，裂缝半长及簇间距相等，取每段2簇裂缝，研究无限与有限导流2种情况下压裂段数对产能的影响。裂缝参数为：裂缝半长100 m，簇间距30 m，裂缝导流能力50 μm2·cm。结果见图6、图7。

图6 无限导流时总产量随压裂段数的变化

图7 有限导流时总产量随压裂段数的变化

由图6和图7可知：①产量随着压裂段数的增加而增加，有限导流时产量对压裂段数的敏感性比无限导流时高；②产量与压裂段数之间并非线性关系，随着压裂段数的增加，产量增加幅度减小，最佳压裂段数为3段6簇。综上结果，进行分段多簇压裂设计时，3段裂缝即可保证较高产量，与文献[1]的数值模拟结果相同。

3 结论

应用位势理论和叠加原理，考虑裂缝无限导流与有限导流 2种情况，推导出分段多簇压裂水平井的产能线性方程组，利用数值分析方法进行求解，得到每簇裂缝的产量，进而求得总的产量。各段裂缝间的距离、每一段内的裂缝半长和裂缝间距均可根据实际情况取值。

裂缝无限导流时，水平井总产量随着所有裂缝半长的减小明显下降，水平井两端的外侧裂缝对总产量贡献最高，同一段内的裂缝，中间裂缝对产量的贡献明显比两侧低。

裂缝有限导流时，产量分布发生变化，水平井两端的外侧裂缝对总产量的贡献减小，同一段内的裂缝，中间裂缝对总产量的贡献明显增大，但产量分布的总体规律与裂缝无限导流时相同，裂缝导流能力对产能的影响比较大，但两者之间并非线性关系。

水平井压裂时，分3段进行压裂、每段2簇即可保证较高产量，压裂设计时应尽量增加裂缝半长与导流能力，重点是水平井两端的外侧裂缝，且裂缝导流能力存在最佳值。符号注释：

Φfm,n(x，y)——裂缝(m，n)在(x，y)处产生的势，cm2/s；x，y——坐标位置，cm；qfm,n——裂缝(m，n)的产量，cm3/s；C——常数；B——体积系数；h——油藏厚度，cm；Lfm,n——裂缝(m，n)的半长，cm；re——油藏供给边界的半径，cm；Φw——井底压力的势，cm2/s；sm——第m段的裂缝数量，条；Φe——供给边界的势，cm2/s；Φ——地层中的势，cm2/s；K——地层渗透率，μm2；p——压力，10−1MPa；μ——地层流体黏度，mPa·s；pe——供给边界处的压力，10−1MPa；pw——井底压力，10−1MPa；Kfi,j——裂缝(i，j)的渗透率，μm2；wfi,j——裂缝(i，j)的开度，cm。

[1] 任龙, 苏玉亮, 王文东, 等. 分段多簇压裂水平井渗流特征及产能分布规律[J]. 西安石油大学学报: 自然科学版, 2013, 28(4):55-59.Ren Long, Su Yuliang, Wang Wendong, et al. Seepage characteristics and productivity distribution of segmented multi-cluster fractured horizontal wells[J]. Journal of Xi’an Shiyou University: Natural Science Edition, 2013, 28(4): 55-59.

[2] Soliman M Y, Boonen P. Review of fractured horizontal wells technology[R]. SPE 36289-MS, 1996.

[3] Love T G, McCarty R A, Surjaatmadja J B, et al. Selectively placing many fractures in openhole horizontal wells improves production[R].SPE 74331-PA, 2001.

[4] 李宗田. 水平井压裂技术现状与展望[J]. 石油钻采工艺, 2009,31(6): 13-18.Li Zongtian. Prospect of horizontal well fracturing technology[J]. Oil Drilling & Production Technology, 2009, 31(6): 13-18.

[5] 陈作, 王振铎, 曾华国. 水平井分段压裂工艺技术现状及展望[J].天然气工业, 2007, 27(9): 78-80.Chen Zuo, Wang Zhenduo, Zeng Huaguo. Status quo and prospect of staged fracturing technique in horizontal wells[J]. Natural Gas Industry, 2007, 27(9): 78-80.

[6] 贾承造, 郑民, 张永峰. 中国非常规油气资源与勘探开发前景[J].石油勘探与开发, 2012, 39(2): 129-136.Jia Chengzao, Zheng Min, Zhang Yongfeng. Unconventional hydrocarbon resources in China and the prospect of exploration and development[J]. Petroleum Exploration and Development, 2012,39(2): 129-136.

[7] 邹才能, 张国生, 杨智, 等. 非常规油气概念、特征、潜力及技术:兼论非常规油气地质学[J]. 石油勘探与开发, 2013, 40(4): 385-399,454.Zou Caineng, Zhang Guosheng, Yang Zhi, et al. Geological concepts,characteristics, resource potential and key techniques of unconventional hydrocarbon: On unconventional petroleum geology[J]. Petroleum Exploration and Development, 2013, 40(4):385-399, 454.

[8] 黄昌武. 页岩油气压裂理论方法和技术体系初步形成[J]. 石油勘探与开发, 2012, 39(4): 443.Huang Changwu. Theoretical methodology and technical system for shale reservoir fracturing[J]. Petroleum Exploration and Development, 2012, 39(4): 443.

[9] 杜保健, 程林松, 黄世军. 致密油藏分段多簇压裂水平井电模拟实验研究[J]. 科学技术与工程, 2013, 13(12): 3267-3270.Du Baojian, Cheng Linsong, Huang Shijun. Study on electrolytic simulation experiment of segmented multi-cluster fractured horizontal well in tight oil reservoir[J]. Science Technology and Engineering, 2013, 13(12): 3267-3270.

[10] 郎兆新, 张丽华. 压裂水平井产能研究[J]. 中国石油大学学报:自然科学版, 1994, 18(2): 43-46.Lang Zhaoxin, Zhang Lihua. Investigation on productivity of fractured horizontal well[J]. Journal of China University of Petroleum: Edition of Natural Science, 1994, 18(2): 43-46.

[11] 张建国, 杜殿发, 侯健, 等. 油气层渗流力学[M]. 2版. 东营: 中国石油大学出版社, 2009: 77-86.Zhang Jianguo, Du Dianfa, Hou Jian, et al. The oil and gas flow in porous media[M]. 2nd ed. Dongying: China University of Petroleum Press, 2009: 77-86.

[12] Mukherjee H, Economides M J. A parametric comparison of horizontal and vertical well performance[R]. SPE 18303-PA, 1991.