移相全桥零电压变换器的建模与控制
孙 琳,曹以龙
(上海电力学院电子与信息工程学院,上海 200090)
移相全桥零电压开关变换器利用谐振电感(包括变压器的漏感)和功率管的并联电容(包括寄生电容)来实现零电压开关,同时实现了PWM控制.该变换器由于具有效率高、功率密度高、低电磁干扰的特性而广泛应用于中大功率场合.[1]
电力电子系统建模分析是系统设计的基础,对变换器系统的分析与设计具有重要意义.移相全桥变换器是由Buck变换器演化而来的,文献[2]中建立了Buck变换器的小信号模型.本文分析了移相全桥变换器与Buck变换器的区别,并在此基础上得出了移相全桥变换器的小信号模型.变换器加入了负反馈构成闭环控制系统,从而提高了变换器的输出精度和动态特性.通过分析控制环路的穿越频率、幅频特性以及相频特性,设计并优化了反馈补偿网络,从而达到了改善变换器稳定性和快速动态响应的目的.
1 移相全桥零电压变换器的小信号模型
移相全桥零电压变换器的拓扑结构如图1所示,其工作原理参见文献[3]和文献[4].
为了推导移相全桥零电压变换器的小信号模型,首先要分析其与Buck变换器的区别.移相全桥零电压变换器利用谐振电感和开关器件的并联电容谐振来实现零电压开关,将造成占空比丢失,这就是移相全桥零电压变换器与Buck变换器的主要差别.变换器实现零电压开关的负载范围与原边谐振电感的大小有关,原边谐振电感的大小又决定了变压器原边电流变化率的大小,从而影响到副边有效占空比的大小和系统的动态特性.
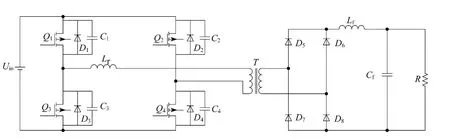
图1 移相全桥零电压变换器的拓扑结构
移相全桥零电压变换器的副边有效占空比为:
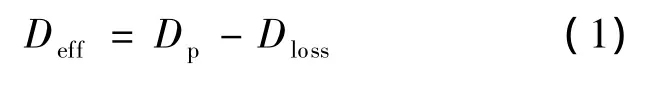
式中:Dp——原边占空比;
Dloss——占空比丢失.
占空比丢失与变压器原边谐振电感、负载大小、开关周期、输入电压有关,因此变换器的小信号模型的传递函数与谐振电感Lr,开关周期T,以及滤波电感电流扰动量,输入电压扰动量和原边占空比扰动量有关.为了对变换器动态特性进行精确建模,需要分析对的贡献,可表示为:
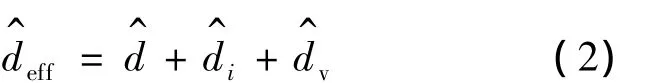
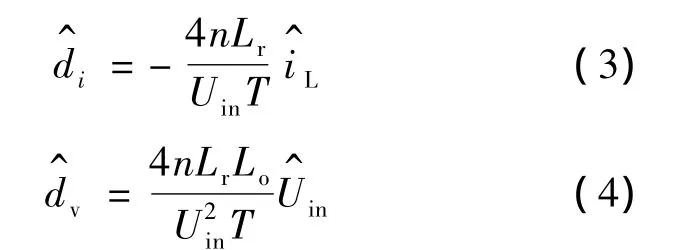
根据文献[2]建立的Buck电路小信号模型,用D代替D,用代替占空比扰动量,用代替输入电压扰动量,即可得到移相全桥零电压变换器的小信号模型,如图2所示.
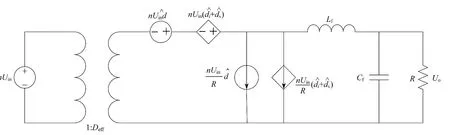
图2 移相全桥零电压变换器的小信号等效模型

式中:f——开关频率;
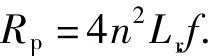
2 补偿网络的分析与设计
2.1 未加补偿环节的系统分析
变换器闭环系统图如图3所示.

图3 变换器闭环系统示意
其中,H(s)为反馈分压网络传递函数,Gc(s)为补偿网络传递函数,Gm(s)为脉宽调制器传递函数.
未加补偿网络时系统的开环传递函数为:
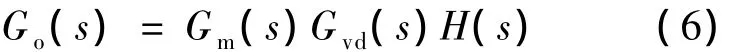
变换器的参数如表1所示.

表1 变换器的电路参数
开关频率为fs=100 kHz,脉宽调制器的三角波幅值为 Um=2.5 V,参考电压 Uref=10 V,H(s)=0.1.将各参数带入Go(s)中得出:

未加补偿网络时,其开环传递函数的幅频特性和相频特性曲线如图4所示.
由图4可以看出,系统的低频增益为4.29 dB,穿越频率为 52.3 kHz,相位裕量仅为 2°,系统的相位裕度太小.系统出现扰动时,会有比较大的输出超调量,同时调节时间也较长,系统的动态响应特性不佳.因此,需要加入补偿网络,以提高相位裕量及增益裕量,使得变换器系统满足静态特性和动态特性的要求.
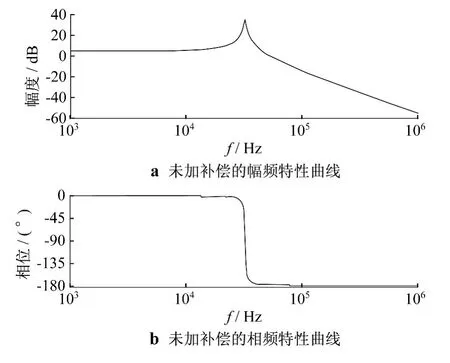
图4 未加补偿网络时系统开环传递函数波特示意
2.2 补偿网络的设计
补偿网络的结构一般分为超前补偿、滞后补偿、超前-滞后补偿3种.[5]本文采用的滞后补偿网络如图5所示.
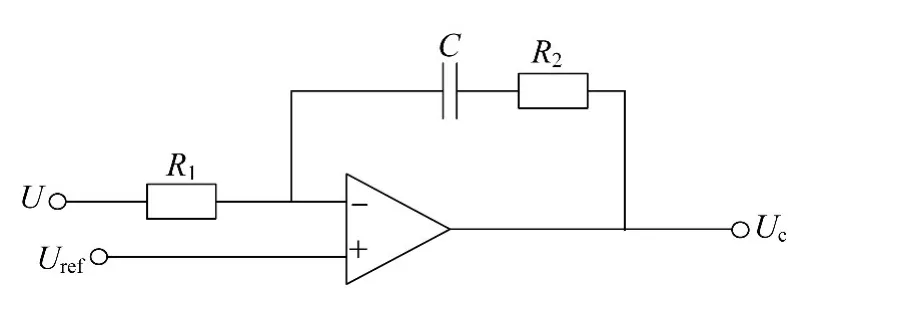
图5 滞后补偿网络结构示意
补偿网络传递函数为:
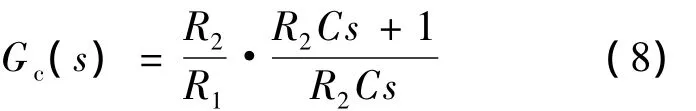
首先,为了提高系统的相位裕量,采用零极点对消,设计由补偿网络的零点去补偿变换器传递函数的一个极点.选取补偿后,开环传递函数的穿越频率 fc=fs/5=20 kHz.取 C=1 nF,R2=35 kΩ,R1=50 kΩ,代入加入补偿网络后的开环传递函数Gc(s)Go(s)中,可得补偿后的波特图,如图6所示.
系统静态开环增益为34.1 dB,穿越频率为20 kHz,相位裕量为62°,满足了系统的稳态和动态要求.
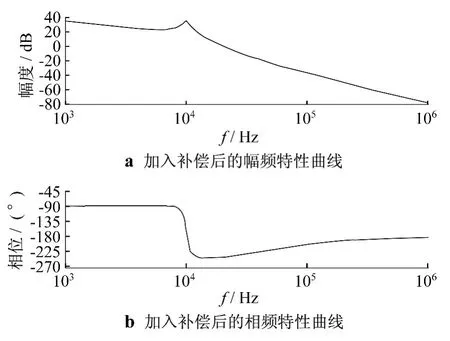
图6 加补偿网络后系统开环传递函数波特示意
3 仿真分析
为了验证补偿网络设计的合理性,对其进行仿真实验.采用Simulink对系统的闭环电路模型进行仿真,仿真参数即为前文设定的参数.负载跃升可以用并入电阻的方式来实现,在0.05 s时闭合开关,并入电阻以调整负载.闭环仿真见图7.
通常称开关管1和开关管3组成的桥臂为超前桥臂,开关管2和开关管4组成的桥臂为滞后桥臂,两种桥臂零电压开关波形如图8所示.图9依次为未加闭环控制和加入闭环控制后负载突变的瞬态响应仿真波形.

图7 系统闭环仿真电路

图8 超前和滞后桥臂零电压开关波形
图8a为经放大后的驱动波形及超前桥臂漏源极电压,可以看出开关管打开前,漏源极电压已经降为零;开关管关断后,漏源极电压线性上升,这说明超前桥臂实现了零电压开关.图8b为经放大后的驱动波形及滞后桥臂漏源极电压,可以看出滞后桥臂也实现了零电压开关.由图9可以看出,加入闭环控制后,系统在负载跃变时的瞬态响应速度很快且稳态效果良好.
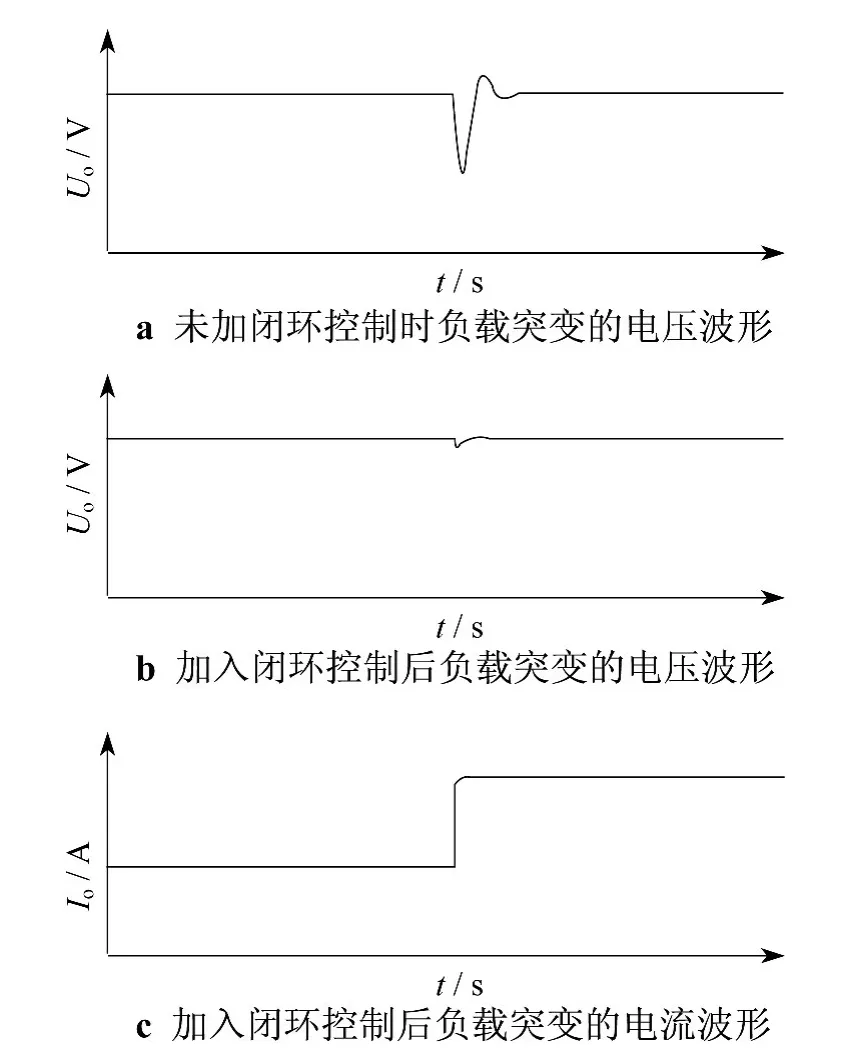
图9 负载突变时的瞬态响应曲线
4 结语
在Buck电路小信号模型的基础上,建立了移相全桥零电压变换器的小信号模型.由小信号数学模型得出了系统传递函数,通过分析控制系统的相频特性和幅频特性设计了系统补偿网络的参数,并加入补偿网络以改善系统在负载突变时的动态性能.利用Matlab仿真验证了补偿网络对系统性能有所改善,以及小信号数学模型的正确性和补偿网络选取的合理性.
[1] 陈仲,石磊,季飚,等.带辅助网络的倍流整流方式全桥ZVS变换器[J].中国电机工程学报,2010,30(30):32-37.
[2] 张卫平.开关变换器的建模与控制[M].北京:中国电力出版社,2006:40-43.
[3] 阮新波,严仰光.脉宽调制DC/DC全桥变换器的软开关技术[M].第2版.北京:科学出版社,2013:44-48.
[4] 杨旭,赵志伟,王兆安.移相全桥型零电压软开关电路谐振过程的研究[J].电力电子技术,1998,32(3):36-39.
[5] 徐德鸿.电力电子系统建模及控制[M].北京:机械工业出版社,2006:101-102.

