非圆齿轮的三维设计与运动分析

吴俊峰，吕小波，李 传，李 波，郑方焱

（1湖北行星传动设备有限公司，湖北 黄冈438000；2武汉理工大学智能制造与控制研究所，湖北 武汉430063）

随着计算机辅助软件（CAD／CAE／CAM 等）、计算机数值计算（Maple等）、图形学技术以及数控加工技术的发展，非圆齿轮的设计制造更容易实现。在实际设计中，非圆齿轮节曲线方程可以通过三种计算方法来确定，即：给定非圆齿轮传动比函数和中心距；给定再现函数和中心距；给定主动齿轮的节曲线方程和中心距［1］。国内许多学者对非圆齿轮的设计及建模做了研究，李福生［2］、黄忠超［3］、郑方焱［4］等提出了设计非圆齿轮的基本方法；胡赤兵［5］等提出了Matlab与ProE相结合对椭圆齿轮进行三维建模；高雪强［6］等通过Solidworks的二次开发结合VB编程研究了椭圆齿轮的实体建模方法；范素香［7］等利用Matlab和UG建立了偏心共轭非圆齿轮的三维实体模型。以上学者设计非圆齿轮的主要方法是利用节曲线进行非圆齿轮的设计，一般用于椭圆齿轮或偏心齿轮的设计，对于一些有特殊运动要求的设计，则比较困难。

本文采用给定的传动比函数和中心距的方法对非圆齿轮进行设计，具有更好的通用性。同时，针对目前非圆齿轮的三维建模方法，采用Solidworks和Matlab相结合的方法，实现了一种非圆齿轮三维实体建模的方法，并利用Solidworks中的Comsom／motion插件对非圆齿轮进行了运动仿真，验证了非圆齿轮理论设计的正确性以及齿轮齿廓啮合性能的优劣。

1 非圆齿轮设计方法及计算公式

本文采用传动比函数对非圆齿轮进行设计，传动比函数可由外加载荷和运动情况推导出来。其外啮合时传动比函数方程为

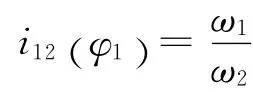
式中ω1，ω2分别为主动轮和从动轮的角速度。为了保证从动齿轮的节曲线是一条封闭的曲线，从动齿轮位置函数φ2（φ1）必须满足φ2（2π）＝2π·n或φ（2π）＝，式中n为整数。从动齿轮位置函数

2计算方程为

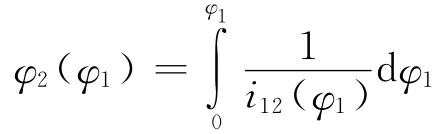
节曲线在非圆齿轮传动中相当于平面齿轮传动中的分度圆，在非圆齿轮的设计制造中可以用节曲线的纯滚动表征非圆齿轮传动。其主动齿轮的节曲线方程

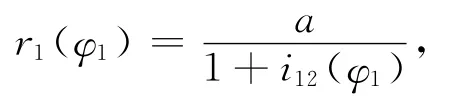
从动齿轮的节曲线方程

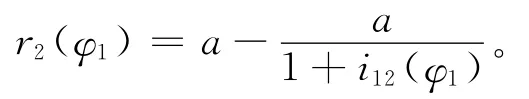
式中a为两齿轮的中心距。由于传动比函数为连续函数，因此节曲线函数同样连续。可以通过平面曲线的曲率公式来验证上述节曲线方程的凸凹性。其曲率公式方程式为

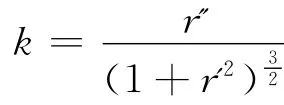
根据曲率公式判断节曲线的凸凹性后，选择不同的加工方式加工齿廓。如果判断节曲线为外凸，可选用插齿或滚齿进行加工；如果判断节曲线为内凹，则只能选用插齿加工。齿轮的中心距和齿数为已知参数，需要进一步确定非圆齿轮的模数。模数可以通过节曲线的周长和齿数来确定，模数的计算方程式为

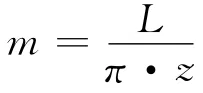
式中：L是节曲线的周长，且

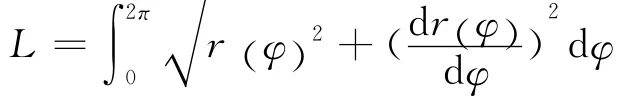
根据计算出的非圆齿轮的模数，选用渐开线滚齿加工方式，再按照齿轮加工的原理，确定齿轮刀具与轮坯的运动关系，得到齿廓方程；进而得到非圆齿轮传动中的其他参数，如齿距、齿厚、齿顶、齿根。齿廓方程中的一段如下：

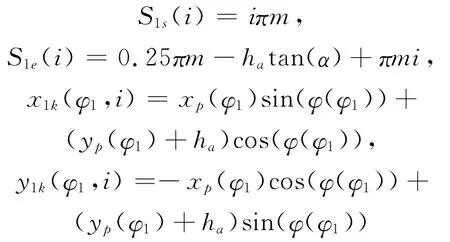
式中：

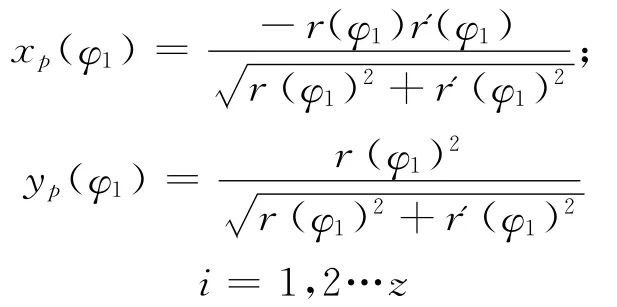
2 非圆齿轮的Maple程序编程及实现方法

在了解了非圆齿轮计算公式推导及各参数意义的基础上进行编程，分别对主、从动非圆齿轮的节曲线、齿顶圆曲线、齿根圆曲线以及齿廓方程进行编程。非圆齿轮的编程流程图见图1。

通过Maple强大的数值处理能力，即可得到非圆齿轮齿廓数据。主动齿轮的设计基本要求是：传动比函数i12（φ1）＝1.41＋sin（φ1），中心距50mm，齿轮齿数20。根据以上要求对非圆齿轮进行Maple编程，其程序片段见图2。

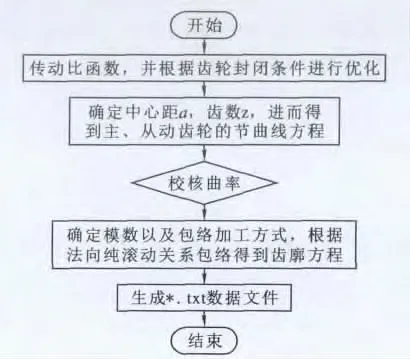
图1 非圆齿轮的编程流程图

图2 Maple程序片段

通过软件绘图工具，得到了主动非圆齿轮和从动非圆齿轮的齿廓形状（图3，图4）。

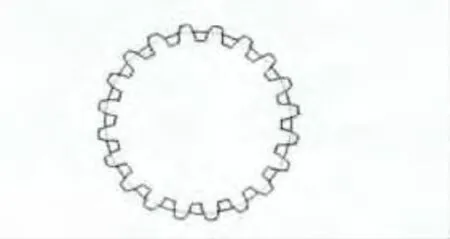
图3 主动非圆齿轮齿廓

图4 从动非圆齿轮齿廓

3 非圆齿轮三维实体建模

将Maple生成的坐标点数据（＊.txt）格式，导入到Solidworks中，可以生成非圆齿轮相应的曲线。在Solidworks的新建模型中，点击菜单栏“插入”中的曲线命令，通过XYZ三个坐标点生成样条曲线。由于所得曲线不能直接进行拉伸，需要在XY平面新建一个草图，再通过“转换实体引用”将曲线转换为实体曲线。在草图对实体线进行修改，再进行拉伸得到非圆齿轮三维实体模型（图5、6）。

图5 主动齿轮图

图6 从动齿轮

4 非圆齿轮运动仿真

利用Solidworks的Comsom／motion插件可以对非圆齿轮传动机构进行运动仿真分析，通过输出从动齿轮的运动性能曲线，如角速度、角加速度以及接触力曲线等，进而得到非圆齿轮对的速度时间响应，并与理论值进行比较，来判断轮齿的啮合性能的优劣性以及设计理论的正确性。

在两个齿轮进行装配之前，先编辑齿轮的材料属性，根据工程机械实际加工齿轮所用的材料，再结合Solidworks自带的材料库中材料，选择AISI 4130钢，其泊松比为0.285，杨氏模量2.05×1011N／m2，密度为7 850kg／m3；其它的参数，如实体的质量等可由软件自动计算。在Solidworks中新建装配图，根据齿轮间的中心距将主动齿轮和从动齿轮进行配合，同时新建两个轴零件，分别与主、从动齿轮进行配合（图7）。

在装配图中新建一个运动算例，在新的运动算例中，确保在MotionManager工具栏中的算例类型为“Motion”分析。在Motion分析中，定义两个轴的约束（将两个轴设置为固定）；再添加碰撞类型，定义主动齿轮和从动齿轮之间接触、主动齿轮与其配合的轴之间接触以及从动齿轮与其配合的轴之间接触，设置刚度为50 000N／mm，最大阻尼为500N·s／m，同时在运动算例属性中允许接触在小距离内的相互渗透。

图7 在solidworks中的装配图

添加一个旋转马达，马达位置选择在主动齿轮中心孔的表面，相对于与主动齿轮配合的轴移动；设置为120°／s（图8），并设置运动仿真时间为8s，25帧／s。最后单击计算运动算例，得到从动齿轮的角速度相应曲线（图9）。

图8 主动齿轮的角速度曲线

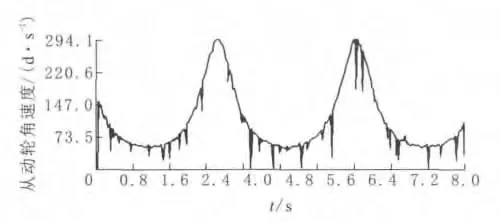
图9 从动齿轮的角速度曲线

从图9可以看出角速度曲线与传动比函数曲线形状基本啮合，图中有部分情况出现失真，比如由于啮合激励的非线性造成的尖点，通过该曲线可以验证设计理论的正确性。

5 总结

1）利用传动比函数设计了非圆齿轮，所设计的非圆齿轮更加精密、稳定。

2）结合Maple强大的曲线编程和数据处理能力，得到了非圆齿轮节曲线、齿廓曲线的坐标点数据。

3）在Solidworks中建立了非圆齿轮的虚拟样机，并通过Solidworks中Motion插件对非圆齿轮进行了运动仿真，验证了理论设计的正确性以及啮合情况的优劣。

［1］ 周 娜，何 丽，许纪倩.基于 MATLAB的非圆齿轮节曲线设计［J］.机电产品开发与创新，2007，20（1）：7－8.

［2］ 李福生.非圆齿轮与特种齿轮传动［M］.北京：机械工业出版社，1983：87－100.

［3］ 黄忠超，蓝兆辉.节曲线封闭的非圆齿轮传动比函数设计［J］.机械传动，2011，35（11）：30－33.

［4］ 郑方焱，陈定方，刘有源.一种非圆齿轮齿廓的通用算法［J］.机械传动，2013，37（04）：64－66.

［5］ 胡赤兵，姚洪辉.基于MATLAB及Pro／E的参数化非圆齿轮设计［J］.机械传动，2010，34（7）：33－35.

［6］ 高雪强，葛骏侠.SolidWorks中的非圆齿轮实体建模方法研究［J］.工程图学学报，2009，（4）：189－192.

［7］ 范素香，齐新华，侯书林.基于Matlab及UG的偏心共轭非圆齿轮的设计［J］.机械传动，2011，35（09）：70－72.