双晶压电悬臂梁电荷输出特性实验研究

刘 阳，罗 奇，孙 科，陶孟伦，陈定方

（武汉理工大学智能制造与控制研究所，湖北 武汉430063）

压电陶瓷是一种能够将机械能与电能相互转换的功能陶瓷材料，具有制作成本和难度低、换能效率高［1］等优点。目前的压电能量收集器在频率匹配、装置结构等技术方面并未完全成熟，本文通过理论建模与仿真分析，设计一种基于PZT－5H压电陶瓷材料的并联式双晶压电悬臂梁，探讨该结构下的电荷输出特性，同时结合实验总结其规律。

1 压电悬臂梁结构及工作原理

压电效应分为逆压电效应与正压电效应。前者是压电片在外电场作用下产生形变，将电能转化为机械能，人们也正是利用这种原理，开发制造出精密电动机、压电泵、超声波电机［2］等装置；后者则是压电材料在外力作用下产生电荷，将机械能转化为电能，本文就是利用正压电效应，研究压电悬臂梁的输出特性。并联式双晶压电悬臂梁（图1）主要由铍青铜金属悬臂梁、PZT－5H压电陶瓷片和支座组成，上下端压电片在粘贴时保证极化方向相同，电路连接时将上下2层压电陶瓷片连接为正极，将电极板作为负极。同时，金属片两端延伸出一部分电极，其中一端与基座固定，另一端随着环境自由振动。

环境中的外部振动激励，会导致悬臂梁受迫振动，发生弯曲变形，进而引起压电陶瓷片内应力与内应变的改变。根据相关的压电理论，压电陶瓷片内部产生应力应变时，其表面将会有自由电荷生成。在这种情况下，压电振子产生弯曲变形，压电悬臂梁的上、下层电极之间会产生一种随外界激励变化而变化的电势差，为负载供电。当环境中的激励频率与悬臂梁的固有频率一致时，将会引起悬臂梁共振，压电陶瓷片的应力与应变在此刻变化达到最大，从而使压电悬臂梁输出的电压变化达到最大。

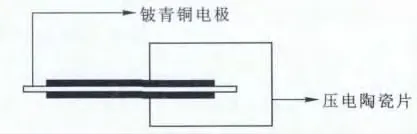
图1 并联式双晶压电悬臂梁结构

2 双晶压电悬臂梁的有限元仿真分析

利用ANSYS软件进行并联式双晶压电悬臂梁的仿真分析是一种结构－电场耦合分析。压电分析考虑到了结构与电场的相互作用，求解由于所施加位移造成的电压分布。

Solid5单元具有三维磁场、热场、电场、压电场和结构场分析能力，并能在各场之间实现有限元的耦合。这里将Solid5单元用于压电材料的建模。Circu94是一个具有压电自由度及正或负电荷贯通变量的电路单元，通过KEYOPT选择，可作为一个线性电阻器、电容器、感应器或一个独立的电压／电流源。这里，Circu94可以与Solid5一起使用，以模拟电路耦合电压分析。支撑层铍青铜片与45钢质量块则采用Solid45单元。不考虑粘接层的影响，并设定支撑层与压电层的位移具有一致性。根据图1及压电悬臂梁相关参数（表1），建立ANSYS模型，进行模态分析求解后得到4阶模态结果：一阶频率f1＝21.705Hz，二阶频率f2＝106.62Hz，三阶频率f3＝290.03Hz，四阶频率f4＝659.71Hz。再进行谐响应分析。频率范围0～1 000Hz，设置0.02的阻尼，走100步，分析完后处理得到的结果如图2所示。

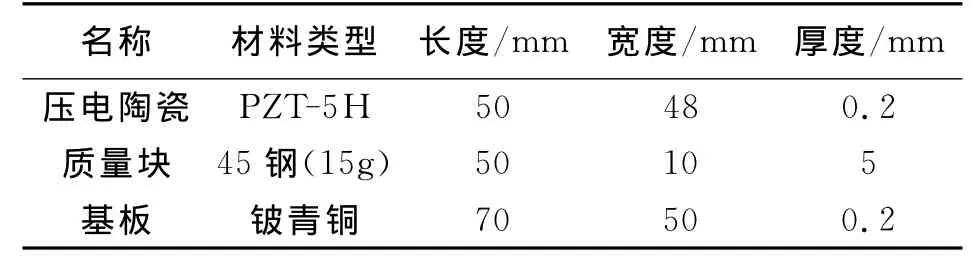
表1 压电悬臂梁相关参数

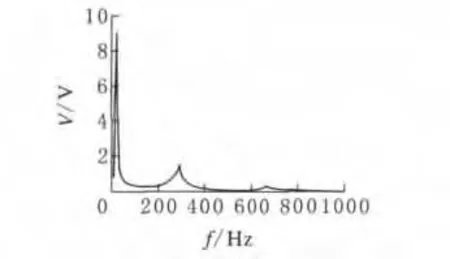
图2 压电悬臂梁谐响应分析

观察可知，输出电压在固有频率附近最大，且一阶固有频率影响最大。为了压电能量收集器的采集效率最大化，应使悬臂梁固有频率尽可能接近外界振动频率。接下来着重分析一阶固有频率附近的输出特性，缩减频率范围至0～100Hz，以提高结果准确性。

悬臂梁末段无质量块时的频率特性如图3所示，可见54Hz时达到最大输出电压2.7V。

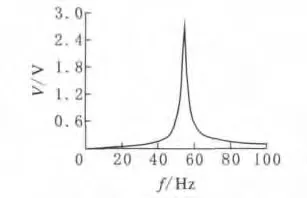
图3 无质量块时频率特性

悬臂梁末段附有一块质量块时的频率特性如图4所示，可见22Hz时达到最大输出电压11.5V。

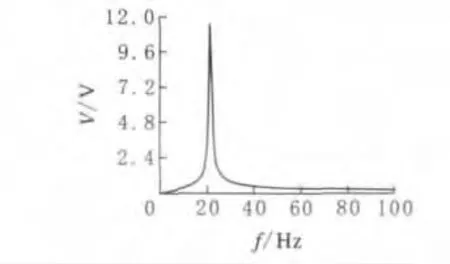
图4 单质量块压电悬臂梁频率特性

比较分析可知，质量块的添加能显著降低悬臂梁结构的固有频率，并提高输出电压值。

3 并联式双晶压电悬臂梁实验

选用的是PZT－5H压电陶瓷片，利用导电胶，将制作的并联式双晶压电陶瓷片与基座绝缘固定后，安装在HEV－2激振器上，使得压电片能与激振器保持同频率的振动。采用GW GFG－8016G信号发生器，将其输出端接入功率放大器，然后连接激振器。这个过程使信号发生器输入的标准正弦波经GF2210功率放大器一定程度放大后，让激振器振动。同时，将功率放大器放大后的激励电压接入HITAC V－212数字示波器CH1端口，利用示波器测出悬臂梁在一定振动激励下的输出电压（图5）。

图5 双晶压电悬臂梁实验装置图

信号发生器产生正弦信号，经功率放大器放大后驱动激振器，带动激振器上的压电悬臂梁振动，电压信号经过示波器输出（图6）。

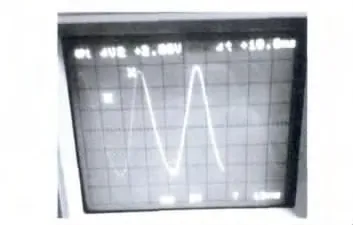
图6 输出电压波形

从图6波形可知，压电悬臂梁在正弦激励的情况下，电压输出也为正弦，并且整体表现稳定，由此可得压电悬臂梁作为电源是可行的。

4 实验结果分析

通过固定信号发生器的正弦信号峰值电压和功率放大器的放大电压，改变激振频率，测量无质量块压电悬臂梁的电压输出频率特性，其结果见图7。由图7可知，在53Hz时，悬臂梁输出电压达到最大，为3V，且电压在固有频率附近变化显著，表明压电材料的输出电压随着振幅的增大而增大，然而，在30Hz与70Hz附近仍有2处波峰突起，经对比分析，此是压电片本身夹持部分的干扰所致。于是，保持相同的激振电压与放大电压的情况下，在悬臂梁的自由端粘接上一定数量质量为15g的质量块，再分别测出它们的频率特性（图8）。

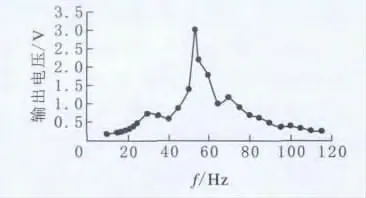
图7 无质量块压电悬臂梁频率特性

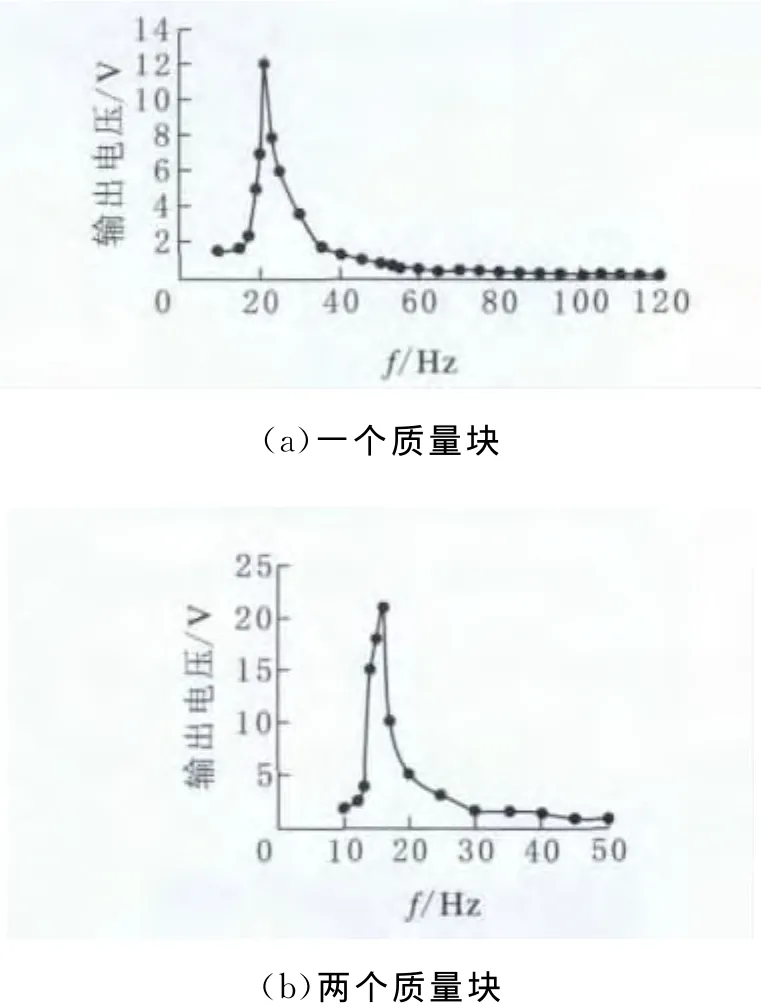
图8 不同质量块双晶悬臂梁频率特性

经过调整，频率曲线完全符合理论规律：末端一个质量块情况下，压电悬臂梁输出电压在21Hz时达到12V峰值；末段有两个质量块情况下，压电悬臂梁输出电压在16Hz时达到21V峰值。图9是三次实验的双晶压电悬臂梁频率特性图。

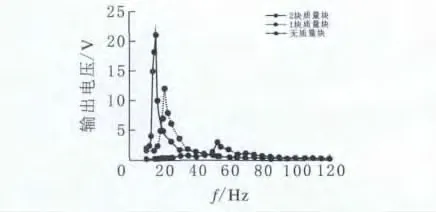
图9 三次实验的双晶压电悬臂梁频率特性

由此可得出结论：在外界激励相同的情况下，双晶压电悬臂梁在共振频率附近输出电压最大，变化最大。末段质量块会降低悬臂梁的固有频率，同时增加同等激励下的振幅，从而增大悬臂梁的输出电压。此后，在电路中接入了1 000Ω的电阻，测量其功率曲线（图10）。

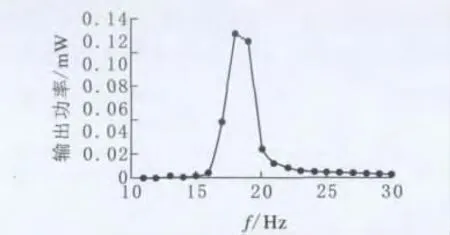
图10 双晶压电悬臂梁功率特性

由测量结果可得出以下结论：压电悬臂梁的功率曲线整体与频率特性曲线规律吻合，在共振频率附近呈现峰值变化，最大输出功率约为0.126mW。

压电悬臂梁在一定环境条件下作为能量收集器的可行性虽得到验证，但其弊端也很明显，后续实验将尝试把多片不同固有频率的压电片连接在一起，人为制造出一组宽频、高电量输出的压电悬臂梁阵列。

［1］ Kwon D W，Gabriel A R.a 2－um BICMOS rectionfierfree AC－DC piezoelectric energy harvester－charger IC［J］.IEEE Transacations on Biomedical Circuits and Systems，2010，4（06）：400－409.

［2］ 曾 平，温建明.新型惯性式压电驱动机构的研究［J］.光学精密工程，2006，14（04）：623－627.

［3］ 袁秋洁.基于压电材料的振动能量收集理论及其结构分析［D］.北京：华北电力大学，2010.

［4］ 党沙沙，许 洋，张红松.ANSYS12.0多物理耦合场有限元分析从入门到精通［M］.北京：机械工业出版社，2010.