二级NGW型行星齿轮传动优化设计方法

朱富贵，周 敏，陈定方

（1武汉理工大学 物流工程学院，湖北 武汉430063；2湖北省烟草公司武汉市公司物流配送中心，湖北 武汉430000）

行星齿轮传动系统由于采用了多个行星轮进行分流，具有结构紧凑、传动效率高、传动平稳等优点［1］，被广泛应用于汽车、航空、船舶以及各种工程机械中，是传动系统的关键组成部件。相同承载能力下，减速机的体积和质量是衡量行星减速器性能好坏的重要指标之一。多级行星传动系统设计参数较多，约束条件复杂，探讨如何有效地进行传动比分配和配齿计算，对减小减速器体积具有重要意义。本文结合螺杆桩机动力头行星减速机的设计，对二级NGW型行星减速器的优化设计模型和方法进行了研究，并将优化结果与通过传统设计方法得到的设计参数进行比较，验证优化方法的有效性。

1 优化数学模型的建立

以二级NGW型行星减速机的体积最小化为目标，行星传动系统强度条件、性能条件、装配条件等为约束条件，建立优化数学模型。图1为二级NGW型行星减速机的传动简图。第一级外啮合中心轮a1与电机相联接，第一级行星架x1与第二级外啮合中心轮a1相联接，第二级行星架x2与输出轴和负载相联接。

1.1 设计变量

给定输入功率P，输入转速n，传动比i，传动比误差Δi，行星轮个数np时，NGW行星齿轮传动系统的设计参数一般取为：模数m，齿数z，齿宽b，变位系数x，啮合角α。通常在建立行星传动系统数学模型时，多选择模数m、齿数za、齿数zc、齿宽b、变位系数xa、啮合角αac、传动比i，作为设计变量［2］；求解过程中，根据传动比约束和安装条件确定齿数zb，根据m ，za，zc，xa，αac确定中心距a，变位系数xb、xc，以及啮合角αbc。但是，根据传动比得到的齿数zb并不一定是整数，即配齿时并不容易取得合适解；根据齿数和啮合角得到的中心距a不一定为整数，而且安装条件是等式约束，使得可行域的性态恶化，不利于优化问题的求解。

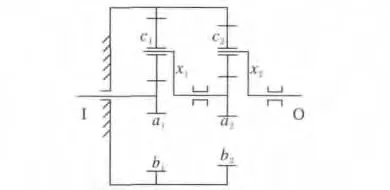
图1 二级NGW型行星减速机传动简图

综合考虑以上问题，将模数m、齿数za、齿数zc、齿宽b、变位系数xa、中心距a作为设计变量，并引入一个由安装条件确定的参数W ，满足

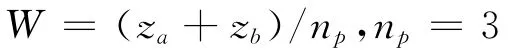
确定设计变量

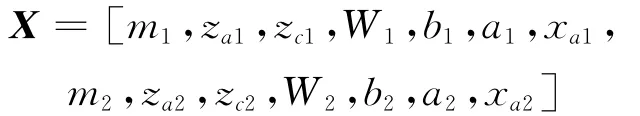
式中：m1、m2为模数；za1、zc1、za2、zc2为齿数；W1、W2为安装条件确定的变量；b1、b2为齿宽；a1、a2为中心距；xa1、xa2为变位系数。

1.2 目标函数

以各级太阳轮和各行星轮总体积作为衡量减速机体积和重量的指标，构造目标函数。模数m、齿数z、齿宽b，是影响齿轮体积的系统级参数；变位系数x、啮合角α、中心距a，是元件级设计参数［3］，能够解除非变位齿轮的同心约束，增多其可能的配齿方案数量。计算齿轮体积时，各齿轮的截面积按标准直齿轮的齿顶圆面积计算。确定目标函数

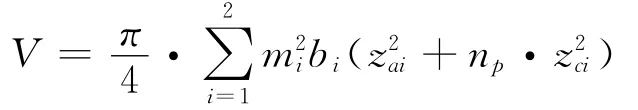
1.3 约束条件

1.3.1 强度约束 NGW型行星减速器中，一般内啮合的强度大于外啮合的强度，故只需校验外啮合中心轮和行星轮的强度作为约束条件，即可保证各齿轮的强度要求。当i≥4时，外啮合中心轮即太阳轮为小齿轮。

1）齿面接触疲劳强度约束

齿面接触疲劳强度

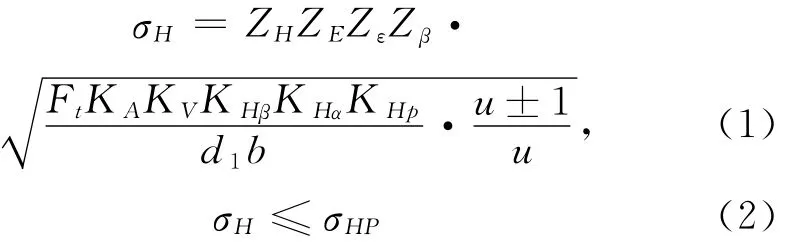
式中，ZH为节点区域系数；ZE为弹性系数；Zε为重合度系数；Zβ为螺旋角系数；KA为使用系数；KV为动载系数；KHβ为齿向载荷分布系数；KHα为齿向载荷分布系数；KHP为行星轮间载荷分配不均匀系数；Ft为分度圆上的名义切向力；d1为工作齿宽，指齿轮副中的较小齿宽；σHP为齿面接触疲劳许用应力。将式（1）变换得

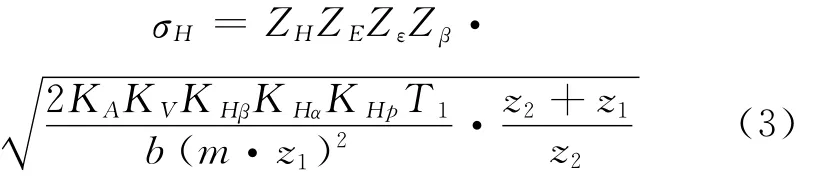
式中，

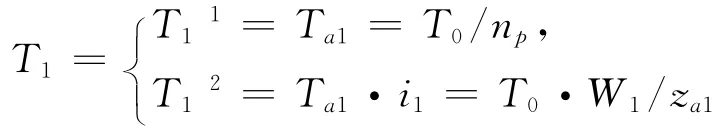
其中，T11为第一级太阳轮输入转矩；T12为第二级太阳轮输入转矩；T0为行星减速机输入转矩；i1为第一级传动比。

2）齿根弯曲疲劳强度约束

齿根弯曲疲劳强度

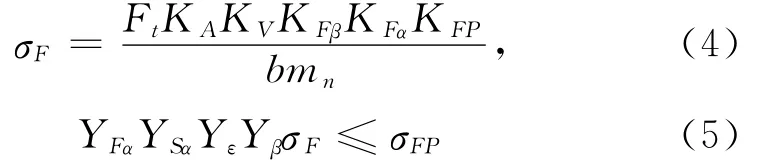
式中，YFα为齿形系数；YSα为应力修正系数；Yε为重合度系数；Yβ为螺旋角系数；KA为使用系数；KV为动载系数；KFβ为齿向载荷分布系数；KFα为齿向载荷分布系数；KFP为行星轮间载荷分配不均匀系数；σFP为齿根弯曲疲劳许用应力。式（4）变换得

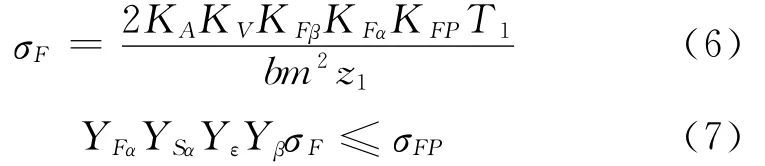
1.3.2 传动比约束

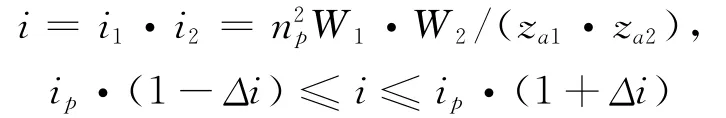
1.3.3 邻接条件约束

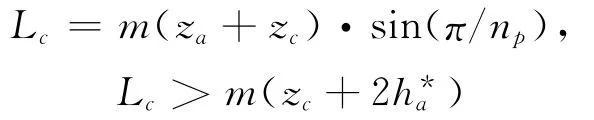
1.3.4 同心约束 NGW型行星传动系统中，为改善内外啮合齿轮副的强度，一般内啮合齿轮副的啮合角为17°～21°，外啮合齿轮副的啮合角为21°～27°。根据同心条件可得

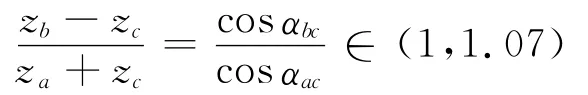
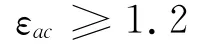
1.3.5 重合度约束 为保证啮合的平稳性，重合度（εac）需要大于一定值。通常取

1.3.6 齿顶厚约束 对于采用正变位的齿轮，需要校核其齿顶厚，以免齿顶过尖。

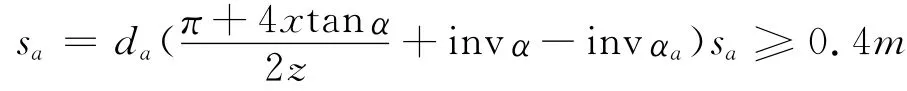
1.3.7 根切约束 为了有效地进行配齿，提高优化效果，采用变位齿轮。为避免根切，变位系数（x）需要满足最小变位系数（xmin）要求，即

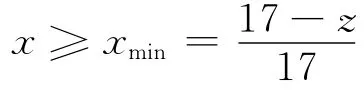
1.3.8 结构尺寸约束 主要包括齿宽约束、外啮合中心轮齿根圆最小直径约束、行星轮最小孔径约束等。结构约束条件根据具体需要加入，在此不一一列举。

1.3.9 边界约束 根据设计者的经验或者在现有数据的基础上，适当确定设计变量的上下限作为边界约束，能够有效减小问题的可行域，加快优化速度，提高调优搜索的效率。

2 优化算法

2.1 混合离散变量的复合形法概述

行星齿轮传动系统的优化设计变量，既有离散型的（如模数m、齿数z、安装参数W），又有连续型的（如齿宽b，中心距a，变位系数x）。但是，为了满足精度、互换性等需要，这些离散变量常取为一系列离散的值。归根到底，涉及的二级NGW型行星齿轮传动系统的优化设计问题是一个单目标、14维混合离散变量、22个约束条件的非线性约束问题。

对于这类工程结构的优化设计问题，借鉴了使用较广泛的混合离散变量的复合形法［4］，其主要思想包括：

1）通过对非均匀离散变量和连续变量的等距离散化处理，将不规则的离散设计空间转化为连续等距的离散值域矩阵Q；

2）一般的复合形法要求复合形的各定点在可行域内，但是对于高维多约束的优化问题，通常难以构造满足该条件的复合形。为了避开寻找可行初始复合形的困难，将目标函数与约束条件整合，得到有效目标函数。定义有效目标函数

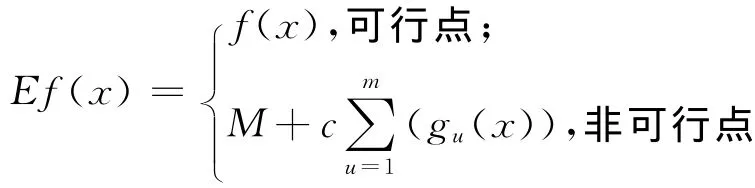
式中：f（x）为原目标函数；M 为一个比f（x）的数量级大得多的常数；c为常数为所有违反约束量的总和。

3）对上述离散值域矩阵和有效目标函数应用复合形法，通过复合形的缩小、反射、重构等方法，进行调优迭代。

4）当满足收敛条件XB＝X0时，将所求得的最好点XB作为初始点，重构复合形并继续调优，直到前后两次调优结果一致，即XB1＝XB2时，则将该点作为离散最优解。

2.2 算法改进

上述方法构造的有效目标函数Ef（x），在设计空间中并非凸函数。将复合形法应用于非凸函数，得到的最优解可能是一个局部最优解，这无疑降低了优化的效率和有效性。为解决该问题，在混合离散变量的复合形法的基础上，提出一种混合离散变量的半随机复合形法。

1）引入随机因子k，构造复合形。在构造复合形时，首先按照复合形顶点的生成方法［5］得到k0（n＋1≤k0≤2n）个顶点，然后由离散值域矩阵Q随机产生k个点Xi，加入到复合形中，最终得到的复合形定点数目为k0＋k。其中

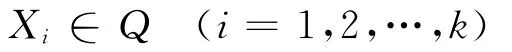
2）增加N，判断终止条件。加入随机点后，当复合形收缩到某一局部最优解时，随机点对搜索方向的改变能够引导复合形跳出局部最优解。由于Xi是随机产生的，所以复合形在保留较优搜索方向的同时也具有一定的随机性。因此，在制定收敛准则时，需要增加最好点相同的次数N，当连续N次得到的最好点趋于一致时，则将该最好点作为离散最优解。即

3 优化结果分析

应用上述混合离散变量的半随机复合形法，对螺杆桩机动力头行星减速机的设计参数进行优化。算法主要参数的设置：K0＝14，k＝14，N＝28。

表1为对二级NGW行星齿轮减速器分别使用传统设计方法、混合离散变量的复合形法、混合离散变量的半随机复合形法，得到的主要参数优化前后的对比。从中可以看出，与传统设计方法相比，复合形法优化后的体积比原体积缩小了8.01%；与传统设计方法相比，半随机复合形法优化后的体积比原体积缩小了10.87%。可见对二级NGW型行星减速机应用半随机复合形法进行优化设计，能够减小减速机的体积，节省原材料，降低成本。

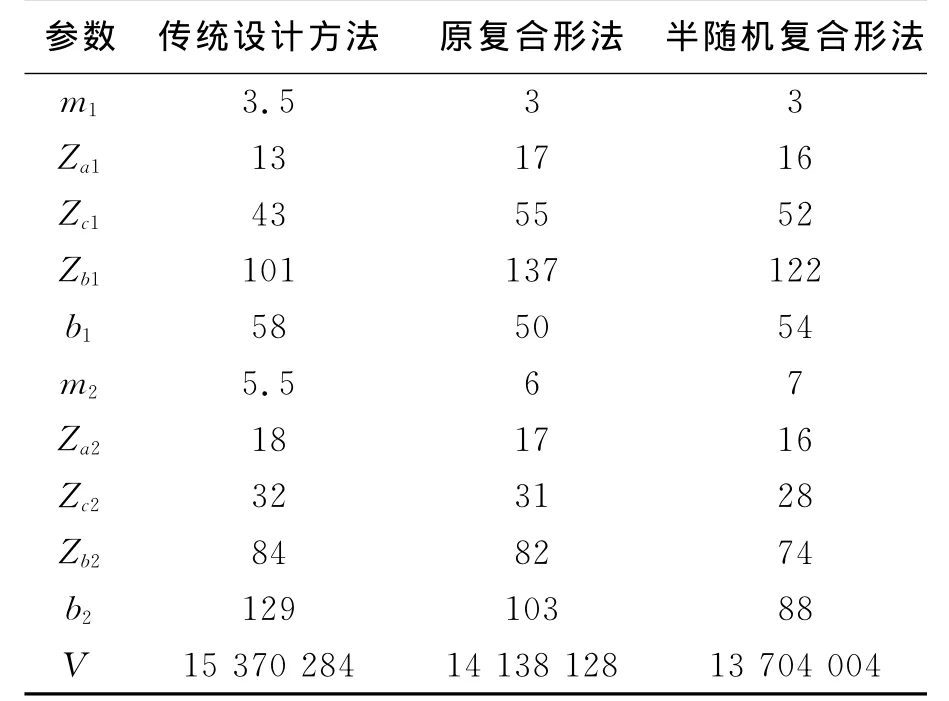
表1 优化结果对比

4 结束语

本文在对二级NGW型行星齿轮传动系统的设计参数进行分析的基础上，使用新的设计变量组合建立了以传动系统体积最小为目标的优化模型。优化得到的最优解可直接应用于工程实际，避免了由于对连续变量优化结果的圆整或近似而导致的优化设计的失败。实例运算表明，提出的混合离散变量的半随机复合形法对于工程结构的混合离散变量优化问题具有参考价值。

［1］ 饶振刚.行星齿轮传动设计［M］.北京：化学工业出版社，2003.

［2］ 渐开线齿轮行星传动的设计与制造编委会.渐开线齿轮行星传动的设计与制造［M］.北京：机械工业出版社，2002.

［3］ 李文博，郭志全.NGW型行星齿轮传动分级优化设计方法研究［J］.天津科技大学学报，2013，28（05）：66－69.

［4］ 王晨曦.工程结构的混合离散变量优化设计［J］.长安大学学报（自然科学版），2002，22（05）：61－64.

［5］ 王晨曦.基于混合离散复合形法的工程优化设计［J］.长安大学学报（自然科学版），2004，24（04）：91－96.