基于改进灰色关联法的高超声速目标威胁评估模型

赵 永，李为民，刘 彬，崔 超

（1.空军工程大学防空反导学院，陕西 西安710051；2.空军工程大学训练部，陕西 西安710051；3.空军驻无锡地区军事代表室，江苏 无锡214063）

0 引言

高超声速目标是指飞行马赫数大于5，以吸气式发动机或组合发动机为主要动力，能在大气层和跨大气层中远程飞行的飞行器。其应用形式包括高超声速巡航导弹、高超声速有人／无人机、空天飞机和空天导弹等多种飞行器。典型的装备有美国的X-51、X-43A、HTV-2、X-37B 等。高超声速目标具有快反应能力、高突防能力、强侵彻能力、精打击能力和低拦截概率等优点［1-2］，其飞行速度快、机动能力较强、隐蔽性能较好，使得现有手段对其探测有限，探测结果可能出现不充分的现象，因而可能出现信息不完全，进而给目标威胁评估带来一定难度，因此迫切需要一种行之有效的量化方法。

目前，应用于目标威胁评估的决策方法有很多，如灰色关联度方法、模糊集方法、Vague集方法、粗糙集方法及熵权方法等等［3-7］。不同的决策方法面对的对象不同，其适用范围也不尽相同。灰色关联分析法（Gray Relation Analysis，GRA）是求解多属性决策问题的一种有效方法，但传统的GRA 是以各因素的样本数据为依据，用灰关联度来描述因素间相关性的强弱，并对序列的各个因素采取等权重法综合，没有考虑目标威胁评估中的确定性和不确定性信息以及决策者对各个指标的偏好程度。文献［8］运用改进灰色关联分析对目标威胁进行评估，但没有考虑样本数据中的不确定性信息和只采用了AHP法进行了主观赋权。即传统灰色关联分析法在确定权重系数时尚存在没有综合考虑样本数据中的确定性和不确定信息以及没有统一主客观赋权的问题。本文针对此问题，提出了基于改进灰色关联分析法的高超声速目标威胁评估模型。

1 高超声速目标威胁评估指标的确定

由于高超声速目标是介于空气动力学目标及弹道导弹类目标之间的一类目标，其威胁评估决策指标可以综合空气动力学目标的决策指标、弹道导弹类目标的决策指标及其自身特点给出。

对于空气动力学目标，其威胁评估问题决策指标一般选取下列几个典型指标：目标类型（目标攻击能力）、目标攻击要地等级、目标的飞临时间、目标的航路捷径、目标的飞行速度及目标的电子干扰能力［4-9］；对于弹道导弹类目标，其威胁评估决策指标一般选取下列几个典型指标：目标射程（目标攻击能力）、目标攻击要地等级、目标的飞临时间、目标的航路捷径、目标的杀伤面积及目标的突防能力［10-11］。

通过比较空气动力学目标的决策指标和弹道导弹类目标的决策指标可以看出，弹道导弹类目标主要在目标射程、目标的杀伤面积及目标的突防能力三方面区别于空气动力学目标。对于高超声速目标，其区分于空气动力学目标的特性在于其速度和高度，其区分于弹道导弹类目标的特性主要在于其机动突防能力、携载能力及攻击的隐蔽性。因此，对于高超声速目标的决策指标主要综合三类目标的共有特性及其自身的专有特点，选取目标的携载能力、目标攻击要地等级、目标的飞临时间、目标的航路捷径、目标的飞行速度及目标的突防能力作为高超声速目标的决策指标。从以上决策指标来看，影响高超声速目标威胁评估的决策指标，既包括定量指标，又包括定性指标，其中目标的携载能力、目标攻击要地等级、目标的突防能力是定性指标，其余为定量指标，并且目标的飞行速度是成本型指标，目标的飞临时间和目标的航路捷径是效益型指标。

2 改进灰色关联法的高超声速目标威胁评估模型的建立

2.1 高超声速目标威胁评估权重的量化

2.1.1 运用熵权理论［12］确定威胁评估指标的客观权

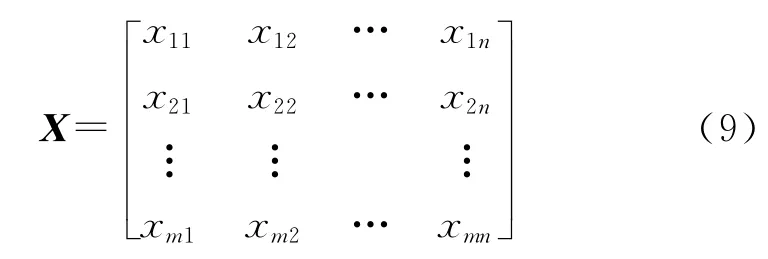
熵是不确定性的一种度量，它还可以度量数据所提供的有效信息量。假设有m 个高超声速目标来袭，记集合为A=（a1，a2，…，am），每个高超声速目标具有n 个威胁指标（属性），组成属性集B=（b1，b2，…，bn），假设第i个高超声速目标对应的第j个威胁指标下的属性值记为uij，对所有属性构成的属性向 量 为ui= （ui1ui2… uin），则m 个 高 超声速目标构成的属性矩阵为：

熵反映了某种状态提供的信息量，定义威胁指标j的熵权为：

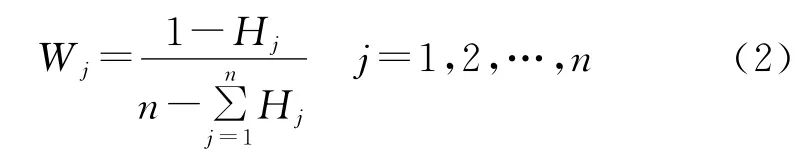
式（2）中，Hj为归一化目标属性矩阵各列向量（属性向量）归一化处理后的矩阵U′中，第j 种属性的熵。

Wo=（W1，W2，…，Wn）称为威胁指标的客观权重向量，其中有0≤Wj≤1。

2.1.2 运用群决策AHP理论确定威胁评估指标的主

1）判断矩阵构造

假设有m 个高超声速目标来袭，每个目标有n个属性。现有l个决策专家依据偏好和个人经验对n个属性进行评估，设第k个专家的判断矩阵为Hk=（）m×n

［13］。决策专家给出的判断矩阵要进行一致性检验，若不满足一致性检验，采用参考文献［14］中方法进行修正。

2）决策专家权重确定

步骤1：设每位决策专家各自为一类，共构造l类G=（G1，G2，…，Gl），令g=l；

步骤2：根据式（3）计算各个决策专家判断矩阵的归一化向量

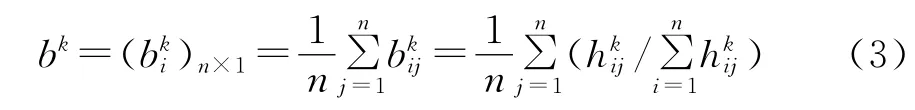
步骤3：根据式（4）计算各类两两之间一致性程度值

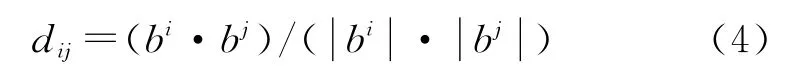
步骤4：选出一致性程度值dij中最大者dxy，并将对应的两类Gx，Gy合并为一个新类Gg+1，即Gg+1=（Gx，Gy）；

步骤5：若g=2（l-1），则转向步骤9，否则转向步骤6；

步骤6：在类集合中去除类Gx，Gy，并加入新类Gg+1；

步骤7：计算所构造的新类两两之间一致性程度值：di，q+1=max｛dix，diy｝，（i≠x，y）

步骤8：返回步骤3 继续合并剩余的类，并令g

=g+1；

步骤9：确定最终得出类的个数和类；

3）目标属性主观权重的计算

令∂f（W）／∂Wj=0，整理得：

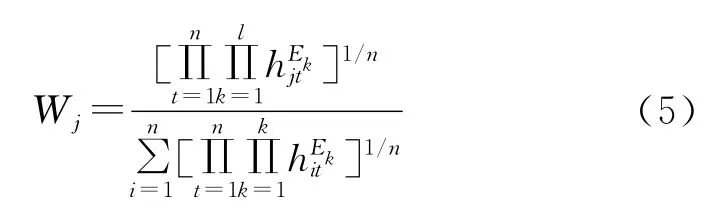
2.1.3 组合权重计算

组合权重计算是指采用加权叠加的方法综合熵权理论的计算结果Wo和群决策AHP 理论的计算结果Ws。令W 为最终计算权重矩阵，α为熵权理论计算结果W1 的权重影响因子，有如下关系：

2.2 灰色关联度求解高超声速目标威胁度

在属性集B=（b1，b2，…，bn）中，分为“成本型”和“效益型”两类属性。采用灰色关联分析法［15］进行研究，需将矩阵U 中属性值按如下规则进行规范化处理，将其化为［0 ，1］ 之间的数值：

灰色关联分析是一种多因素统计分析方法，它是以各因素的样本数据为根据，用灰色关联度来描述因素间关系的强弱、大小和次序等。如果样本序列反映出两因素变化的态势基本一致，则它们之间的关联度较大；反之，关联度较小。

第i个评价方案的第j 个属性，与参考属性集X0的第j个指标的关联度定义为：

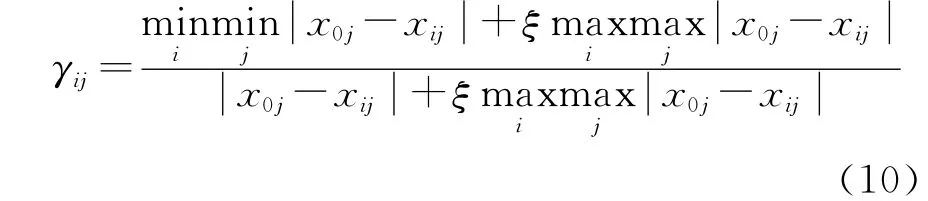
其中，ξ∈（0，1）为分辨系数。通常ξ=0.5，则可得关联矩阵：

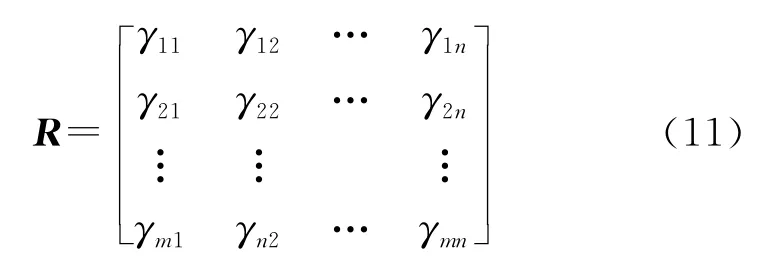
2.3 威胁评估矩阵的计算

威胁评估指利用组合权重矩阵将目标评估矩阵中的各指标值加权叠加，评出不同目标的代数值，利用求得的代数值的大小对目标的威胁程度进行排序，求得威胁程度最大的目标。假设威胁评估矩阵为E，则有如下计算公式：

每个威胁目标在威胁评估矩阵中均有一个对应的值，这个值就是对应目标的威胁程度大小，通过比较不同威胁目标的威胁评估值得出高超声速目标的威胁排序，从而确定威胁程度最大的目标。

3 仿真实例

假设在某次空天防御作战中，有6批来袭目标对某要地实施攻击，通过空天多传感器获取目标信息如表1。

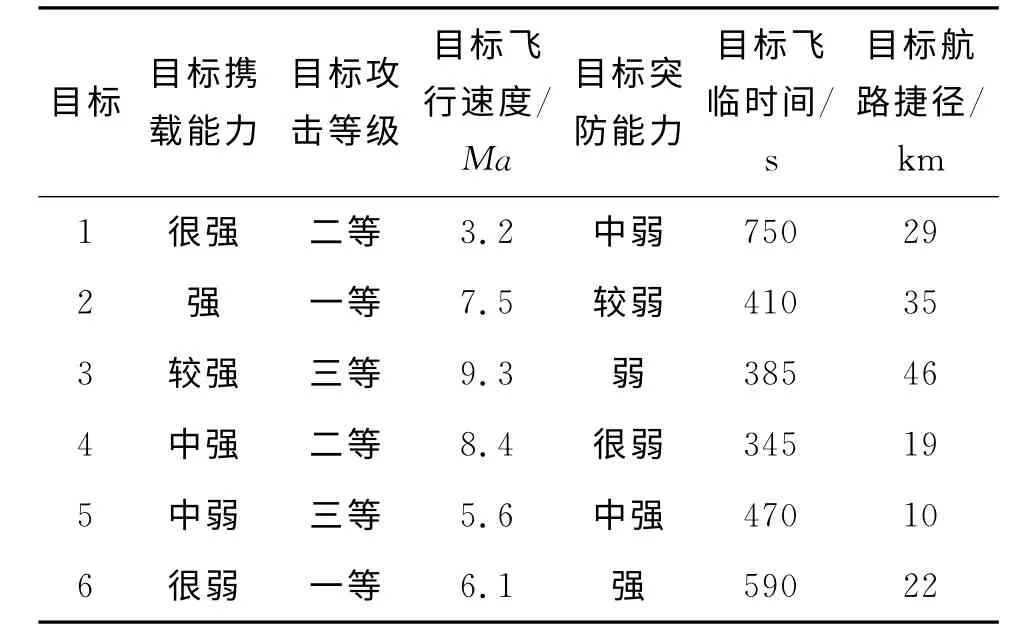
表1 高超声速目标威胁评估信息参数表Tab.1 Hypersonic targets'threat evaluation information parameters

对于高超声速目标威胁评估中的定性指标可以由专家对各指标进行评价，并赋予［0，1］之间的小数。定性指标对应量化取值大小如表2、表3所示。

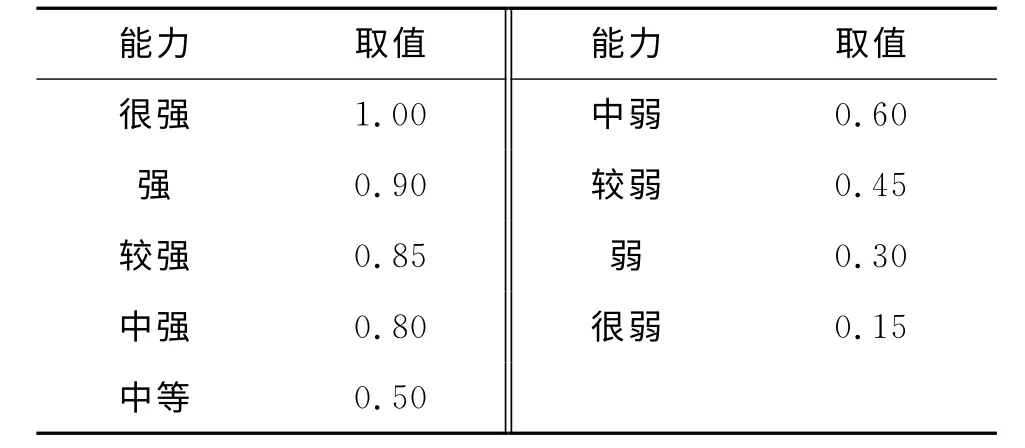
表2 能力量化取值Tab.2 Value-taking for ability quantization

表3 等级量化取值Tab.3 Value-taking for grade quantization

1）高超声速目标威胁评估指标主客权重计算

根据表1、表2、表3，构造出决策矩阵U。

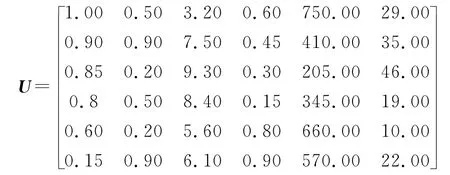
根据式（7）（8），将U 进行规范化处理，得规范化矩阵X。

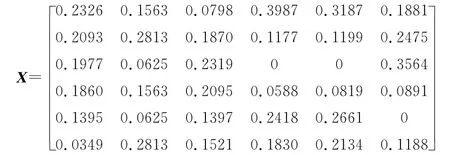
设共有4名决策专家运用AHP法对目标威胁评估指标进行评价，得到以下4个判断矩阵：

对4个判断矩阵进行一致性检验，其一致性指标分别为：0.0941 2，0.0843 2，0.073 12，0.075 81，均小于0.1，满足一致性要求。

根据式（3）求出各个判断矩阵的归一化向量为

b1=（0.407 1，0.145 3，0.168 5，0.082 6，0.066 3，0.130 2）T；b2= （0.392 7，0.151 4，0.158 3，0.085 5，0.060 5，0.151 6）T；

b3=（0.332 9，0.089 4，0.169 3，0.064 1，0.102 4，0.241 9）T；b4= （0.391 3，0.112 3，0.069 1，0.079 2，0.135 1，0.212 9）T。

有4位专家参加评判，所以先将专家分成4类，即G1=｛E1｝，G2=｛E2｝，G3=｛E3｝，G4=｛E4｝，令g=4。

根据式（4）得出两两决策专家之间的一致性程度值 分 别 为：d12=0.998 3，d13=0.952 1，d14=0.952 9，d23=0.961 3，d24=0.960 5，d34=0.965 9。

从计算结果可以看出，d12=0.998 3的值最大，所以将类G1，G2合并成一个新类G5，G5=｛G1，G2｝=｛E1，E2｝，此时的剩余类为G3，G4，G5，计算各类之间的一致性程度值，得d35=max｛d13，d23｝=0.961 3，d45= max｛d14，d24｝=0.960 5，d34=0.965 9，g=g+1=5；依据聚类分析步骤，将剩余的各类依次聚合，得到新类G6=｛G3，G4｝=｛E3，E4｝，G7=｛G5，G6｝=｛E1，E2，E3，E4｝。

将4位专家分成两类较为合适，第一类有2位专家，分别为E1，E2，第二类有2 位专家，分别为E3，E4，则E1=E2=E3=E4=2／（2+2+2+2）=0.25，所以决策专家的权重为E=（0.25，0.25，0.25，0.25）。

根据式（5）求得高超声速目标威胁评估指标主观 权 重 为：Wo1= （0.211 9，0.159 7，0.163 6，0.142 4，0.146 7，0.175 7）。

运用熵权法，根据式（2）求解高超声速目标威胁评估指标客观权重为：

Ws=（0.184 1，0.157 7，0.165 5，0.162 8，0.160 7，0.169 1）

2）关联矩阵R 的计算

步骤1：构建参考序列和比较序列

X0=（1.0，0.9，9.3，0.9，205.0，10.0）；X1=（1.0，0.5，3.2，0.6，750.0，29.0）；X2=（0.9，0.9，7.5，0.45，410.0，35.0）；X3=（0.85，0.2，9.3，0.3，205.0，46.0）；X4=（0.8，0.5，8.4，0.15，345.0，19.0）；X5=（0.6，0.2，5.6，0.8，660.0，10.0）；X6=（0.15，0.9，6.1，0.9，570.0，22.0）。

其中，X0为参考序列，X1，X2，X3，X4，X5，X6为比较序列。

步骤2：求各序列的初值像

X′0=（1.0，0.9，9.3，0.9，205.0，10.0）；X′1=（1.0，0.5，3.2，0.6，750.0，29.0）；X′2=（1.0，1.0，8.3，0.5，455.6，38.9）；X′3=（1.0，0.2，10.9，0.4，241.2，54.1）；X′4=（1.0，0.6，10.5，0.2，431.3，23.8）；X′5=（1.0，0.3，9.3，1.3，1 100.0，16.7）；X′6=（1.0，6.0，40.7，6.0，3 800.0，146.7）。

步骤3：求差数列

Δ1=（0，0.4，6.1，0.3，545.0，19.0）；Δ2=（0，0.1，1.0，0.4，250.6，28.9）；Δ3=（0，0.7，1.6，0.5，36.2，44.1）；Δ4=（0，0.3，1.2，0.7，226.3，13.8）；Δ5=（0，0.6，0，0.4，895.0，6.7）；Δ6=（0，5.1，31.4，5.1，3 595.0，136.7）。

步骤4：求两极差

M=3 595.0，m=0

步骤5：求关联矩阵R

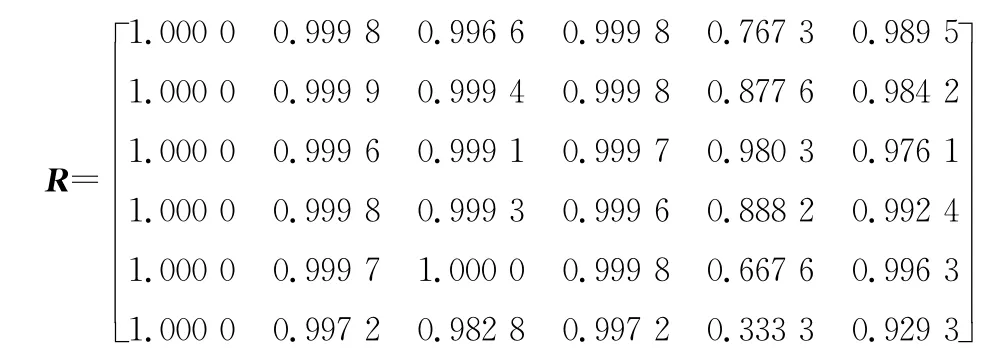
3）计算威胁评估

根据不同主客观权重影响因子求解威胁评估排序如表4所示。5种不同权重影响因子的最终解算所得的威胁评估排序均为m3＞m4＞m2＞m1＞m5＞m6。由排序结果可知，在此次作战想定中，目标3的威胁值最大，应优先考虑打击。一般情况下，采用α=0.5进行威胁评估排序解算。在客观信息比较容易获得、数据准确性比较高的情况下，宜采用4）进行求解，反之，采用2）进行计算。1）和5）分别为仅采用群决策AHP和熵权法确定高超声速目标威胁评估指标权重进行目标威胁评估排序。

表4 不同组合权重下的威胁评估排序Tab.4 Threat evaluation sorting in different combination weights

4 结论

本文提出了基于改进灰色关联分析法的高超声速目标威胁评估模型。该模型结合高超声速目标与空气动力学目标和弹道导弹类目标的共性特点以及其自身特点，确定了高超声速目标威胁评估指标；综合考虑了主观和客观因素，运用群决策AHP 法和熵权法分别求解出威胁评估指标的主客观权重，并融合得到组合权重，更加突出体现指标的模糊性和不确定性，使评价结果更具可信度。仿真表明，该模型的排序结果与专家结果基本一致，对抗击高超声速目标作战决策具有一定的指导意义。

［1］王还乡，李为民，上官强，等.高超声速飞行器巡航段拦截作战需求分析［J］.战术导弹技术，2012（2）：36-40.

［2］马丽，杨建军，张维刚.高超声速飞行器发展综述［J］.飞航导弹，2012（6）：22-27.

［3］Evans G W.An Overview for Techniques for Solving Multi-objective Mathematical Programs［J］.Management Science（S0025-1909），1984，30（6）：1268-1282.

［4］夏璐，邢清华，范海雄.Vague物元及熵权的空袭目标威胁评估［J］.火力与指挥控制，2012，37（2）：84-88.

［5］耿涛，卢广山，张安.基于Vague集的空中目标威胁评估群决策方法［J］.系统工程与电子技术，2011，33（12）：2686-2690.

［6］郭辉，徐浩军，周莉.粗糙集和区间数空袭目标威胁评估［J］.火力与指挥控制，2011，36（9）：46-54.

［7］谷向东，童中翔，郭辉，等.IAHP 和熵权相结合的TOPSIS法的空战目标威胁评估［J］.火力与指挥控制，2012，37（1）：69-72.

［8］王百合，黄建国，张群飞.基于改进灰关联分析的目标威胁评估模型研究［J］.计算机工程与应用，2008，44（4）：212-215.

［9］李春芳，赵虹，巴宏欣，等.基于多属性分类决策的空中目标威胁评估模型［J］.指挥信息系统与技术，2011，2（6）：55-58.

［10］张鑫，万新敏，李争，等.运用AHP 和云重心评价法的弹道导弹威胁评估［J］.空军雷达学院学报，2010，24（5）：340-343.

［11］罗亮，刘健，朱永水.基于层次熵模型的弹道导弹威胁评估［J］.现代防御技术，2012，40（6）：76-80.

［12］Kenzo Kurihara，Nobuyuki Nishiuchi.Efficient Monte Carlo Simulation Method of GERT-type Network for Project Management［J］.Computers ＆Industrial Engineering（S0360-8352），2002，42：521-531.

［13］吴云燕，华中生，查勇.AHP 中群决策权重的确定与判断矩阵的合并［J］.运筹与管理，2003，12（4）：16-21.

［14］华中生，吴云燕，徐晓燕.一种AHP判断矩阵一致性调整的新方法［J］.系统工程与电子技术，2003，25（1）：38-40.

［15］刘思峰，党耀国，方志耕，等.灰色系统理论及其应用（第五版）［M］.北京：科学出版社，2010.