ARIMA模型在手足口病预测预警中的应用

李 标 李雪梅 古丽斯

深圳市盐田区疾病预防控制中心，深圳盐田 518000

为增加手足口病防控工作的主动性和预见性，及时、科学地对手足口病的发病趋势进行预测是很重要的。[1]时间序列分析法中的自回归滑动平均混合模型是由博克思(Box)和詹金斯(Jenkins)于70年代初提出的著名时间序列预测方法,近年来由于其在公共卫生领域良好的适用性而逐渐被广大学者重视[2]。

1 资料与方法

1.1 资料来源

数据源于中国法定传染病报告系统—“中国疾病预防控制信息系统”，选取现住址为深圳市盐田区，发病日期为2008年1月1 日—2014年4月30 日的所有临床诊断和实验室确诊手足口病病例。人口数来源于每年深圳市盐田区统计局公布的人口数。

1.2 建立模型基本原理与方法

AR IMA 模型的基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。其中ARIMA（p，d，q）称为差分自回归移动平均模型，AR 是自回归，p 为自回归项；MA 为移动平均，q 为移动平均项数，d 为时间序列成为平稳序列所做的差分次数（阶数）。

所有试验数据均使用SPSS 19.0 软件包处理，并确保准确无误。组间的差异以P＜0.05 表示具有统计学意义。

2 结果

2.1 序列平稳化检验

绘制2008年1月—2014年4月深圳市盐田区手足口病发病率的时间序列图，时间单位定义为年月型，起始点为2008年1月。结果显示，总体线性趋势不明显，5～6月，9～10月出现明显季节性高峰。提示原始序列非平稳序列，进行一阶逐期差分和一阶季节差分后，得到一个基本稳定的序列。

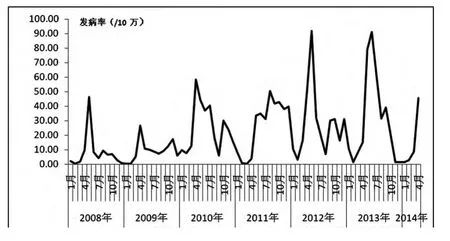
图1 深圳市盐田区2008年1月—2014年4月手足口病发病率的时序图

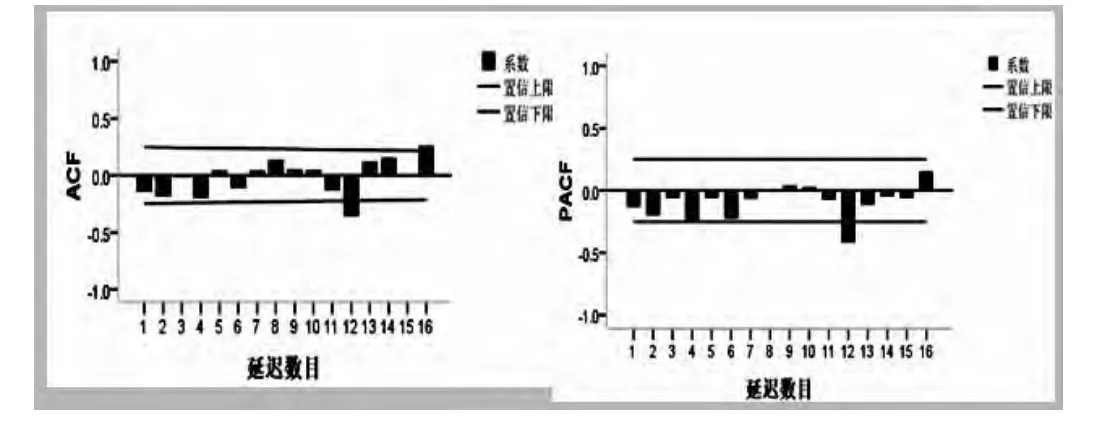
图2 原始序列1 阶差分，1 阶季节性差分后的自相关及偏相关图

2.2 模型识别与定阶

尝试建立ARIMA (p,d,q) (P,D,Q)模型,经过前述对数据进行一阶差分和一阶季节差分的预处理，获得较平稳数列,因此,d=D=1。自相关图显示（见图2 左侧）,所有阶以后函数值除周期点处外都落入区间内,所以q 取为0,而12 函数不为0,可以取Q 为1。

偏自相关图（见图2 右侧）,可取p 为0,而12 阶函数不为0,P 可以取0 或1。综合序列自相关系数和偏自相关系数的性质，初步选定ARIMA(0，1，0)（1,1,1）12 或ARIMA(0，1，0)（0,1,1）12。

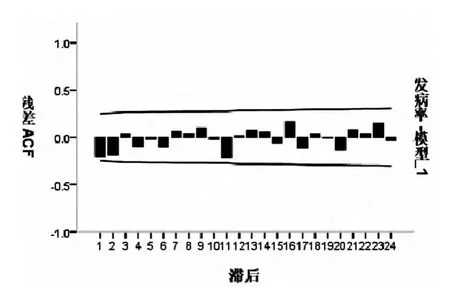
图3 残差自相关函数分析

2.3 模型检验及优化

通过比较平稳的R2，BIC，LB 检验统计量，模型ARIMA(0，1，0)（0,1,1）12 的BIC=6.066，在拟合比较的模型中最小，故选定为最佳模型。模型的参数估计值有统计学意义。（见表1）残差白噪声检验，自相关系数均在95%可信区间，提示用该模型进行预测是合理的。（见图3）4.拟合曲线与预测效果评价

用模型ARIMA (0，1，0)（0,1,1）12 对2013年9月—2014年4月各月发病率进行拟合，并用实际发病率进行比较，相对误差的中位数为0.71，各月相对误差以2013年11月最大，为6.09.提示模型虽可用于对深圳盐田区手足口病发病趋势进行预测，但是个别月份预测的精度仍存在较大误差。

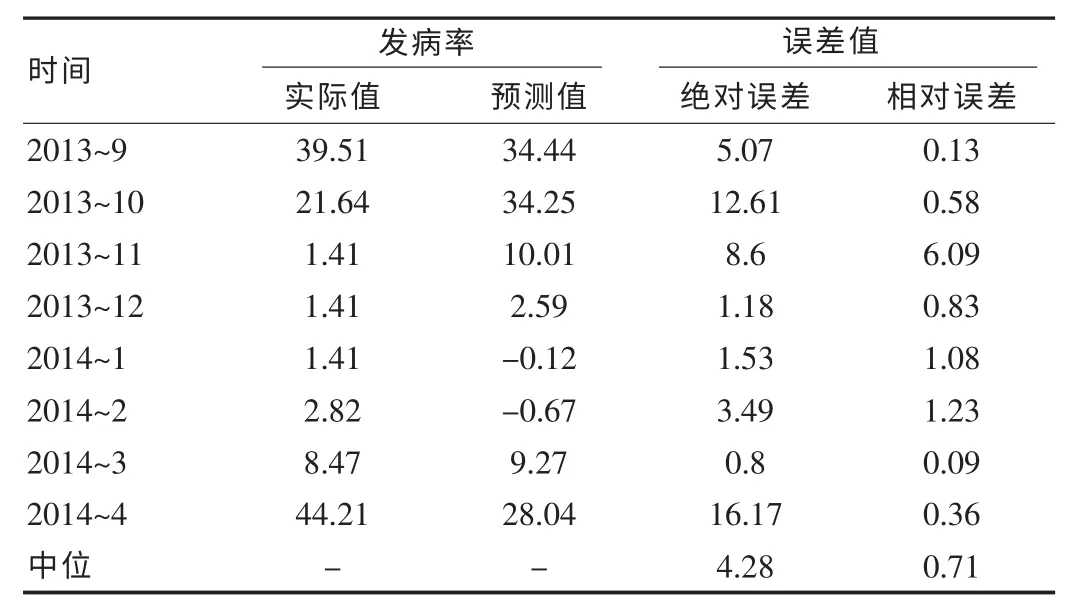
表1 2013年9月—2014年4月手足口病实际发病率与预测发病率比较

2.5 模型预测

以2008年1月—2014年4月深圳盐田区手足口病发病率数据为基础，用模型ARIMA (0，1，0)（0,1,1）12 对2014年5～12月该地区手足口病发病率进行预测，结果显示5～6月会出现高峰，分别为76.48/10 万和61.25/10 万。9～10月有个小高峰，分别为45.04/10 万和44.93/10 万。（见图4），见表2。

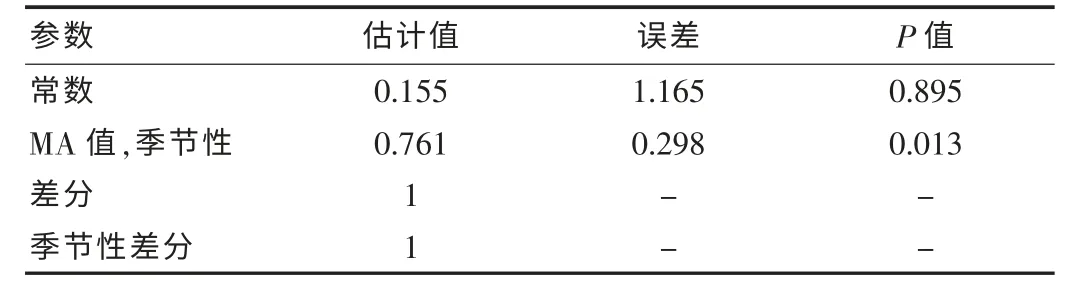
表2 2014年12月手足口病发病率预测情况

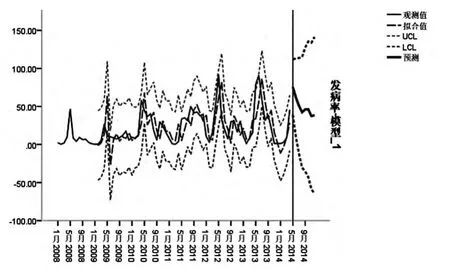
图4 深圳盐田区2014年5月—2014年12月手足口病发病率预测情况

3 讨论

ARIMA 模型是目前应用较多的时间序列预测方法之一，它综合考虑到了疾病的季节性、周期性、随机性等可能影响序列平稳性的因素，提高了模型的拟合和预测效果，同时借助，模型的参数进行了量化表达，在传染病预测中具有广泛的适用性[2]。彭志行,陶 红等将ARIMA 模型应用于麻疹疫情的预测预警，为防控提供了积极的指导作用[3]。陈莉.运用SPSS 软件建立ARIMA 模型，很好的拟合了海南省细菌性痢疾的发病趋势[4-5]。吴孟泉等应用ARIMA 模型对山东省2009年3月30 日—8月30 日手足口病发病时间序列进行拟合，结果证明该时间段手足口病发病率预测值符合实际发病率的变动趋势[6]。手足口病具有传染性强，传播途径多，病原学复杂，各病原体间无交互免，患者可多次重复感染等特点，容易在短时间造成大面积流行[1]。因此较准确的预测手足口病的发病趋势，及时制定防控措施，对于减少聚集性及暴发疫情的发生是非常重要的。

本文利用2008年1月—2013年9月深圳市盐田区手足口病发病资料，通过识别、估计、诊断等过程拟合建立了ARIMA(0，1，0)（0，1，1）12 预测模型。利用2013年10月—2014年4月实际发病数与预测发病数进行比较，实际值与预测值相对误差的中位数为71%，实际值均落入95%可信区间，提示手足口病的发病无异常增高，且发病的趋势与实际情况基本一致。表明利用ARIMA 模型预测深圳市盐田区手足口病发病趋势的可行性。另一方面也显示了预测的实用性和应用价值，根据发病率既往的变化规律(线性趋势、季节性、周期性等)，如果实际发病率在预测值95%可信区间范围内波动，表明当月疫情基本正常，如果超出预测值95%可信限范围，应提示并警惕传染病的暴发或流行的可能，可以为传染病预警预报及干预提供依据[6-7]。根据预测结果，2014年5～12月深圳市盐田区手足口病的发病率有2 个高峰，分别为5～6月，9～10月，提示在此期间，需重点做好手足口病的防控，尤其是加强与托幼机构、医疗机构的联防联控，较少聚集性或暴发疫情的发生。

本次研究所建立的模型只是对深圳市盐田区2014年手足口病发病率的预测模型,而对今后几年的预测，应该在不断收集新的数据基础上，再对其修订或重新建模[8-10]。因为手足口病的发病率受到诸多未知随机因素的影响,所建立的模型更适合进行短期的预测,

[1]蔡小虹，万秋萍，吴益生，等ARIMA 模型预测上海市打闸北区手足口病发病趋势[J].实用预防医学，2012,19（3）：381-384.

[2]彭志行，鲍昌俊，赵扬，等.ARIMA 乘积季节模型及其在传染病发病预测中的应用[J].数理统计与管理，2008，27(2) :365-367.

[3]彭志行,陶红,贾成梅,等.时间序列分析在麻疹疫情预测预警中的应用研究[J].中国卫生统计,2010,10(27):459-461.

[4]冯丹,韩晓娜,赵文娟,等.中国内地法定报告传染病预测和监测的ARIMA.模型[J].疾病控制杂志,2007,11(2):140-143.

[5]陈莉.探讨ARIMA 模型在细菌性痢疾发病预测中的应用[J].中国卫生统计，2011,8(28):417-419.