新的无证书签密方案

马陵勇，卓泽朋，廉玉忠

(1.东莞理工学院城市学院 计算机与信息科学系,广东 东莞 523106；2.淮北师范大学 数学科学学院， 安徽 淮北 235000)

新的无证书签密方案

马陵勇1，卓泽朋2，廉玉忠1

(1.东莞理工学院城市学院 计算机与信息科学系,广东 东莞 523106；2.淮北师范大学 数学科学学院， 安徽 淮北 235000)

提出了一种新的无证书的签密方案，新方案在签密过程中只需要1次配对运算，在解签密过程中仅需要4次配对运算．与已有方案相比，新方案具有更高的效率．在安全性方面，新方案满足机密性、不可伪造性和可公开验证性．

无证书签密；双线性对；可公开验证性；可追踪性；计算Diffie-Hellman问题

0 引言

Riyami A I和Paterson K首次在文献[1]里提出无证书公钥密码体制．不同于基于身份的密码体制(用户的密钥由可信中心产生)，无证书的密码体制中，用户的密钥是由可信中心和用户自己分别独立生成，这就解决了基于身份密码体制中的密钥托管问题[2]，同时也不存在传统公钥中的证书管理．

在传输信息的过程中，需要保证信息的机密性，同时还要保证信息的可认证性．对传输的信息加密，可以实现机密性，而签名可以达到认证性．如果需要对传输的消息同时保证机密性和认证性，传统做法是对消息“先签名后加密”，但该方法不仅效率低下，而且成本很高．1997年，Zheng在文献[3]里提出签密的概念，它在一个方案中可以同时实现机密性和认证性要求，与原有机制相比，签密机制通常效率较高，是一种比较理想的数据安全传输方法．文献[4],[5],[6],[7]各自提出了有效的无证书签密方案，多数无证书签密方案中都用到了双线性对运算，双线性配对运算的速度相对群中的乘法运算和指数运算是非常慢的，因此，一个方案的运行效率主要取决于算法中使用双线性配对运算的次数．本文提出一种新的无证书签密方案，新方案在签密阶段只需要一次对运算，解签密阶段只需要4次对运算，具备更高的效率．同时，新方案满足可公开验证性．

1 预备知识

定义1双线性映射

G1是一个阶为素数q的加法循环群，P是一个生成元；G2是一个阶为q的乘法循环群．我们把满足以下三个条件的映射e:G1×G1→G2叫做双线性映射

(2)非退化性：存在U，V∈G1，使得e(U,V)≠1G2．

(3)可计算性：对于任意的U，V∈G1，计算e(U,V)的值是容易的．

定义2计算Difiie-Hellman问题(CDHP)

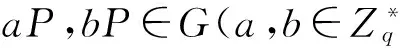
定义3计算双线性Difiie-Hellman问题(CBDHP)

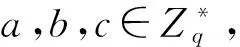
2 新的无证书签密方案

2．1 新方案的构造

在文献[8]中的无证书签名算法的基础上，本文建立一种新的签密方案，新方案是无证书的，具体描述如下：

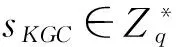
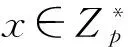
(3)用户公钥设置：身份为ID的用户设置自己的公钥PID=xP．

(4)用户的部分私钥生成：对身份为ID的用户计算QID=H1(ID‖PID)，由KGC计算ID的部分私钥SID=sKGCQID，并安全的传输给用户ID．

(5)设置用户私钥：用户ID的私钥为(SID，x)，公钥为(PID,QID),

(6)签密：假设发送方Alice的身份信息为IDA，公钥为(PA，QA)，私钥为(SA,xA)，接收者Bob的身份信息为IDB，公钥为(PB，QB)，私钥为(SB，xB)，Alice执行以下步骤对消息m进行签密：

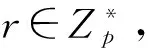
②计算k=H2(R,T,W,IDA,IDB)

③计算c=Ek(m)

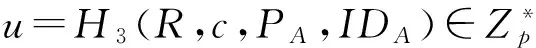
⑤计算V=ruSA+xAQA

Alice输出消息m的密文σ=(R,c,V)

(7)解签密：收到Alice发来的密文σ=(R,c,V)，接收者Bob执行以下步骤对密文解签密：

①计算u=H3(R,c,PA，IDA)

②验证e(P,V)=e(PPub,R)ue(PA，QA)是否成立，若成立，则签名是合法的，继续执行，若不成立，则解签密过程终止．

③计算T=e(R,SB),W=xBR，并计算对称加密所使用的密钥k=H2(R,T,W,IDA,IDB)．

④恢复出消息m=Dk(c)

2.2 方案的正确性

(1)可解密性

接收者Bob可以计算T=e(R,SB)=e(rP,sKGCQB)=e(sKGCP,QB)r=e(Ppub,QB)r，W=xBR=xBrP=r(xBP)=rPB，从而可以恢复对称加密的密钥k，也就可以恢复出明文m.

(2) 可验证性

e(P，V) =e(P,ruSA+xAQA)=e(P,rusKGCQA)e(P,xAQA)

=e(sKGCP,rQA)ue(xAP,QA)=e(PPub,R)ue(PA，QA)

(3)可追踪性

由于e(SA，aP)=e(sKGCQA,aP)=e(sKGCH1(IDA‖PA),aP)=e(H1(IDA‖PA)，PPub)a

所以合法的用户总可以证明自己的清白，从而可以追踪积极不诚实的KGC的假冒．

3 新方案的安全性与性能分析

3.1 安全性分析

3.1.1 认证性

文献[8]中的签名方案已经在标准模型下证明了在CDHP假设下的不可伪造性，而我们的签密方案是将消息m加密后的密文c进行签名,敌手如果要伪造合法密文，必须要伪造对c的签名，而这相当于解决CDHP问题，所以我们的方案满足可认证性．

3.1.2 机密性

无证书密码系统中有两类潜在的攻击者，第一类攻击者不知道用户部分私钥，但是它能够随意替换用户的公钥，第二类攻击者可以获得系统主密钥．在签密阶段，方案只有在c=Ek(m)用到了消息m，敌手想要从密文中恢复出消息m，只有对c进行解密．假设选取的对称加密算法(E，D)是安全的，敌手需要获得对称加密的密钥k．而Hash函数H2具有单向性，所以攻击者必须计算出T和W的值．

第一类攻击者能够任意替换用户的公钥，所以W的值可以计算．攻击者在掌握(P，R，QB，PPub)的情况下，计算T=e(PPub,QB)r的值，由于不能获得用户部分私钥，这相当于解决CBDHP问题．

而第二类攻击者可以获得系统主密钥，所以容易计算出T的值，但是由于无法知道接收者部分私钥，因而，计算W=rPB，相当于解决CDHP问题．

所以，对两类攻击者来说，新方案在CBDHP问题和CDHP问题难解的假设下，均能满足机密性的要求．

3.1.3 可公开验证性

在本文方案中，由于最后的密文σ=(R,c,V)包含了验证密文合法性所需要的知识，因此，任何用户都能够通过解签密的步骤来验证密文的合法性．新方案满足可公开验证性．

3.2 方案的性能分析

我们从通信成本和计算量方面对新方案做一个评价．下表给出了几种无证书签密方案的效率比较，为了方便，我们用e代表方案中的一次双线性配对运算，Ex表示方案中做的在群G2中的一次指数运算，而Mu表示群G1中的一次加法运算．双线性配对运算的速度相对群中的乘法运算和指数运算是非常慢的，因此，一个方案的运行效率主要取决于算法中使用双线性配对运算的次数．如表所示，尽管签密阶段新方案的运行效率与文献[5,6,7]中的方案大体相当，但是在解签密阶段，新方案减少了一次双线性配对运算，在运行效率方面有了一定提高．

几种无证书签密方案的效率比较表

4 结束语

基于文献[8]中的无证书签名方案提出了一种新的无证书签密方案，并对新方案进行了安全性和性能分析，与目前已有的签密方案相比，我们提出的新方案在运行效率方面有了一定提高． 设计运行效率更高的无证书签密方案，是需要进一步研究的工作．

[1]S.Al-Riyami,K.Paterson.Certificateless public key cryptography[C]//Laih C S,Proceedings of the Asiacrypt 2003,Taipei,Taiwan,2003,2894:312～323.

[2]A.Shamir.Identity based cryptosystems and signature schemes[C]//LNCS 196:Proceedings of Crypto’84.Berlin:Spinger-Verlag,1984:47～53.

[3]Y.Zheng.Digital signcrypion or how to achieve cost(signature & encryption )<

[4]Y.Han.Generalization of Signcryption for Resources comstraomed Environments[J].Wireless Communication and Mobile Computing,2007,7(7):919～931.

[5]M.Barbosa,P.Farshim.Certificateless signcryption[C]//Proceedings of ASIACCS’08.New York:ACM,2008:369～372.

[6]F.Li,M.Shirase,T.Takage.Certificateless hybrid signcryption[C]//LNCS 5451:Proceedings of ISPEC’09.Berlin: Springer-Verlag,2009:112～123.

[7]陈 虎，宋如顺，张福泰.无证书并行签密方案[J].计算机工程与应用，2009，45(21)：85～87.

[8]王丽莎，张建中.一种高效安全的无证书数字签名方案[J]计算机工程与应用，2012，48(15)：70～73.

NewCertificatelessSigncryptionScheme

MALing-yong1,ZHUOZe-peng2,LIANYu-zhong1

(1.Department of Computer and Information Sciences,City College of Dongguan University of Technology,Dongguan 523106,China;2.School of Mathematical Science,Huaibei Normal University,Huaibei 235000,China)

A certificateless signcryption scheme is proposed.New scheme only requires one pairing operation in the signcryption phase and four pairing operations in the unsigncryption phase.Compared with the existing schemes,the new scheme is more efficient.For security requirements,this new scheme satisfies confidentiality,unforgeability and public vertifiability.

certificateless signcryption;bilinear pairing;public verifiability;trace ability;Diffie-Hellman problem

梁怀学)

2014-06-02

安徽省自然科学基金项目(1208085QF119);东莞理工学院城市学院青年教师发展基金项目(2014QJY002Z)

马陵勇(1978-)，男，河南省泌阳县人，现为东莞理工学院城市学院讲师，硕士.研究方向：密码学及信息安全.

TP309

A

1674-3873-(2014)03-0093-03