一种新的致密气藏平均毛管压力计算模型

杨 宇，周 文，林 璠，贺承祖，张 昊，曹 煜

（油气藏地质与开发国家重点实验室（成都理工大学），成都610059）

致密砂岩气储层较常规储层非均质性强，孔隙结构复杂，渗透率低，如何评价致密砂岩气储层的孔隙结构一直是一项重要的研究课题。Brooks和Corey根据大量的岩心实验结果，认为毛管压力与归一化润湿相饱和度在双对数坐标上是线性关系［1］。但是Lekia在统计致密砂岩气藏的岩心后指出，Corey的统计规律仅仅适用于渗透率较高的储层，并不适合致密储层。对于致密砂岩气藏这种低渗储层，在双对数坐标中，毛管压力曲线与含水饱和度是线性关系［2］。

20世纪80年代，德国数学家Mandelbrot创立了分形几何学［3］，能够用来研究复杂的现象。随后的二三十年时间里，分形理论广泛运用于岩石孔隙结构的描述分析中，特别是结合毛管压力曲线来研究岩石孔隙结构［4－6］。本文通过分形理论对毛管压力曲线进行分析，并且对Lekia的观点进行论证。

1 毛管压力模型

1.1 Brooks-Corey毛管压力关系式

根据大量岩心统计数据，Brooks和Corey总结出毛管压力（pc）和归一化润湿相饱和度）之间存在下列经验关系［1］

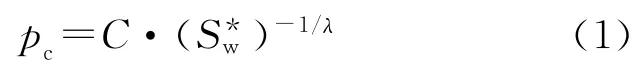
其中，归一化润湿相饱和度（）定义为

式中：λ为多孔介质孔隙大小分布指数；C为常数；Sw为润湿相饱和度；Swi为束缚水饱和度；pc为毛管压力。

对方程（1）两边分别取对数，便可得到双对数坐标中pc与之间的线性关系式

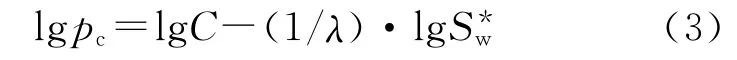
将pc和画在双对数坐标上，能够得到方程（3）样式的拟合直线段的表达式，通过斜率可以求得多孔介质孔隙大小分布指数λ。λ是反映储层孔隙结构的重要特征参数，可用于储层结构分析和油水两相相对渗透率等的计算中。

但是，Wells和Amaefule研究发现，上述pc与之间的关系仅仅适用于渗透率较高（一般＞0.01μm2）的砂岩，而对于孔隙度和渗透率较低的致密气藏却并不适用［7］。Lekia根据美国和加拿大的致密气藏岩心压汞数据，进一步总结出毛管压力和润湿相饱和度在双对数坐标上呈线性关系［2］

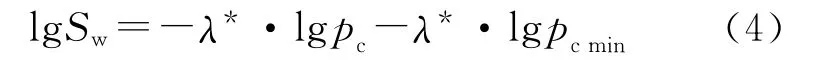
式中：λ＊为孔径分布指数；pcmin为排驱压力，是储层中最大连通孔隙对应的毛管压力，其中pcmin≥pd。

1.2 基于分形理论的毛管压力模型

20世纪80年代，德国数学家Mandelbrot研究发现并创立了能够用来描述复杂孔隙结构的分形几何理论［3］。近年来，分形理论已广泛运用于孔径分布的描述中［8］。根据分形理论，孔隙体积与孔径的关系为

式中：r为孔径；V为孔径为r的孔隙体积；D为分形维数，取值范围一般在2～3之间。

方程（5）两边分别对r求导

于是，孔径大于r的累计孔隙体积可以通过对方程（5）积分求得

连通孔隙总体积（Vt）为

式中：rmax为储层中最大连通孔隙半径；rmin为储层中最小孔隙半径。

在注入非润湿相驱替润湿相的过程中，汞先流入大孔隙，再进入小孔隙。在某一注入压力下，汞的注入体积就等于孔径大于r的孔隙的累积体积。可以定义非润湿相在孔隙体积中所占的百分数，即：非润湿相饱和度（Snw）为

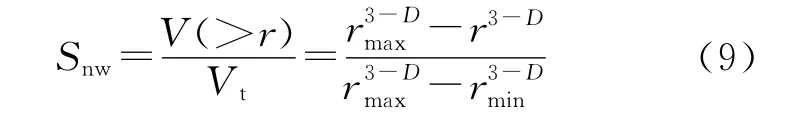
根据Laplace方程，毛管力与孔径的关系为

式中：σ为表面张力；θ为润湿接触角；r为孔径。

将方程（9）代入方程（8）中，得到非润湿相饱和度为

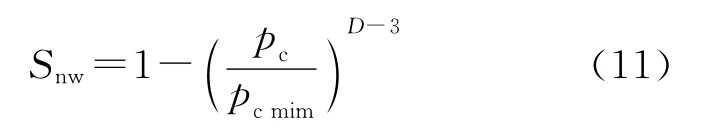
于是，润湿相饱和度为

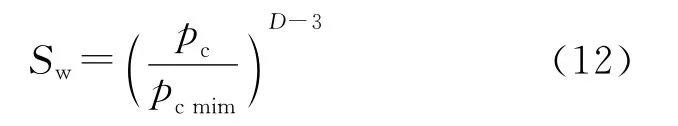
方程（11）两边取对数，即得到双对数坐标中毛管压力和润湿相饱和度之间的线性关系为［8］

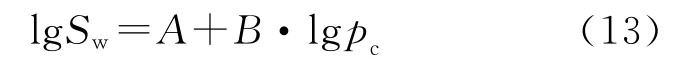
其中

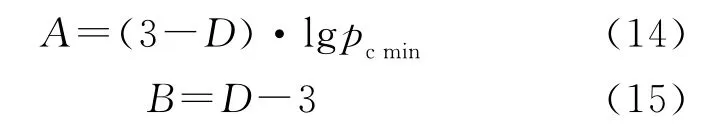
显然，方程（13）和方程（4）在本质上是相同的。方程（13）还可转换为指数关系式

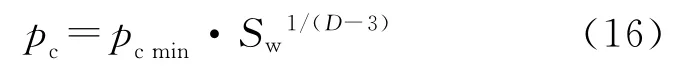
2 毛管压力模型的对比

作者测试了川西北地区致密砂岩气藏压汞曲线。其中3组样品毛管压力数据见表1。

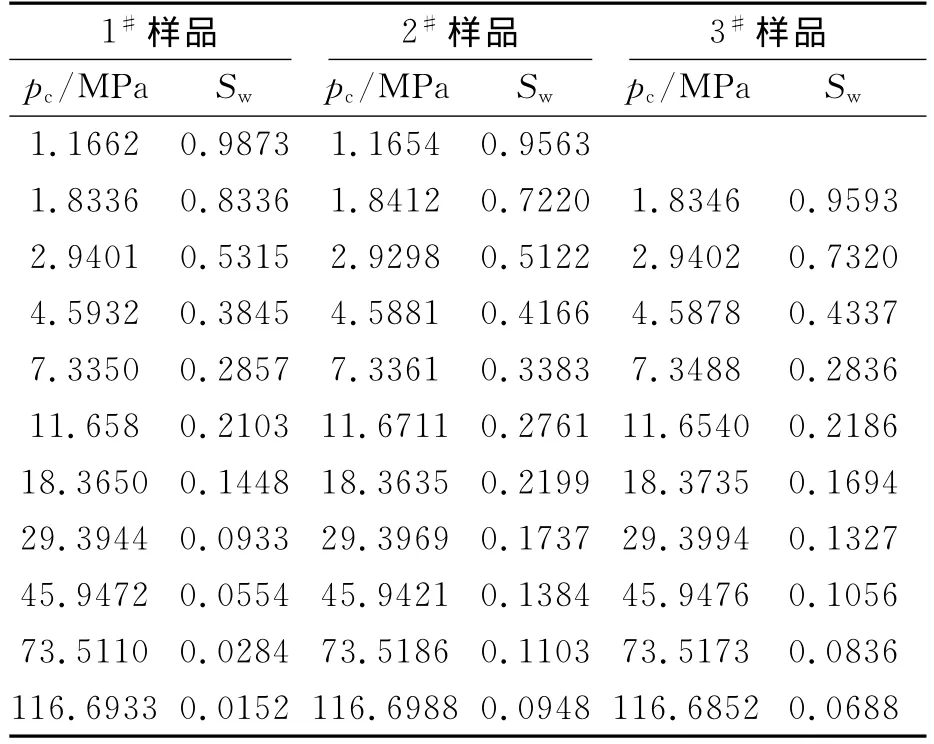
表1 3组样品毛管压力数据Table 1 Capillary pressure data of three tight gas sandstone reservoir core samples

根据毛管压力数据，分别绘制出3组样品的毛管压力与归一化含水饱和度双对数曲线以及毛管压力与含水饱和度的双对数曲线（图1）。

由3组样品的毛管压力曲线可以看出，对比于毛管压力与归一化含水饱和度的双对数曲线关系，毛管压力与含水饱和度的双对数曲线线性关系更加明确，拟合程度更高；而毛管压力与归一化含水饱和度的双对数曲线往往为一条有弧度的曲线，从而进一步证明了Lekia的观点。

此外，对3组样品的双对数曲线进行拟合，能够得到形如方程（12）的线性方程，利用线性方程中的斜率，可以求得3组样品的分形维数。1＃样品的分形维数为2.1，2＃样品为2.5，3＃样品为2.4。3组样品的分形维数均在合理值范围内，充分证明了利用压汞法得到的毛管压力与含水饱和度的双对数曲线能够计算分形维数，分析岩石中复杂的孔隙结构。

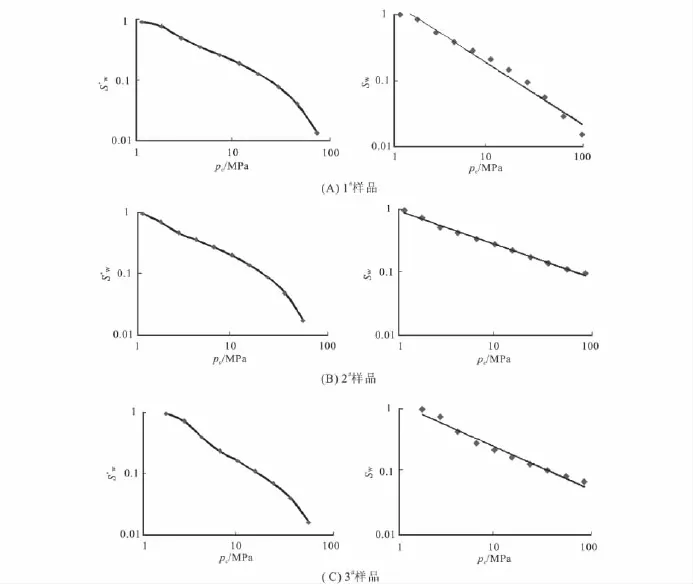
图1 样品毛管压力与归一化含水饱和度双对数曲线、毛管压力与含水饱和度双对数曲线Fig.1 Log-log plot of versus pcand Swversus pc

3 排驱压力与分形维数对毛管压力曲线的影响

根据方程（16）可以认为毛管压力曲线的形态与两个变量有关：排驱压力和分形维数。其中，任何一个变量改变，都会造成毛管压力曲线在形态上的变化。

如果分形维数不变，改变排驱压力，毛管压力曲线的变化见图2。

排驱压力是评价岩石储集性能的主要参数之一。一般情况下，孔隙度高、渗透率大的储层排驱压力大，孔隙度低、渗透率小的储层排驱压力小。由图2可以看出，在分形维数一定的情况下，毛管压力曲线随着排驱压力的降低曲线下移，说明储层孔喉歪度越粗，储集性能越好。

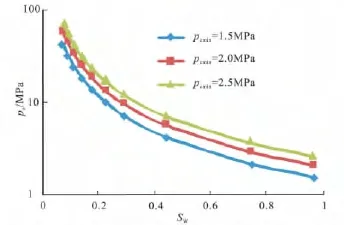
图2 不同排驱压力条件下的毛管压力曲线（D＝2.2）Fig.2 Capillary pressure curves under different displacement pressures

如果排驱压力不变，改变分形维数，毛管压力曲线的变化见图3。

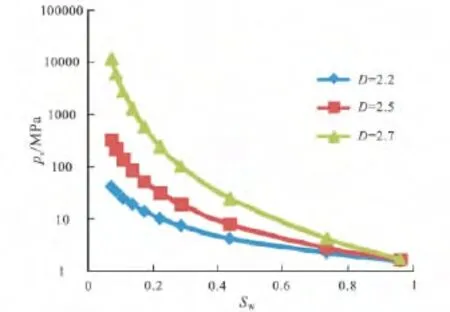
图3 不同分形维数条件下的毛管压力曲线Fig.3 Capillary pressure curves under different fractal dimensions（pc＝1.5MPa）

由图3可以看出，在排驱压力相同的情况下，随着分形维数的增加，曲线的平坦段越短，曲线越陡峭，表明分形维数的大小与孔隙结构的分布有紧密联系：分形维数一般在2～3之间，越接近2，储层的储集性能越好；反之，分形维数值越接近3，储层储集性能越差［9，10］。

4 平均毛管压力曲线计算

在实际测试毛管压力曲线时，通常会对同一类储层中多个岩心进行毛管压力测试。由于孔隙结构和渗透率不同，所以测得的毛管压力曲线形态也不同。根据不同毛管压力曲线，计算得到表征同类储层的平均毛管压力曲线，对于储层分析以及油藏工程计算有着重要的意义。利用本文中提出的毛管压力模型，计算平均毛管压力曲线的具体步骤如下［11］。

（1）拟合每一种样品的双对数曲线，得到形如方程（13）的线性关系式

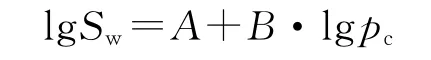
（2）求得每一种样品的A、B、D和pcmin，其中pcmin由方程（14）求得，并且利用算术平均的方法计算出它们的平均值和

（3）将计算得到的平均值代入方程（16），把数据画在pc－Sw坐标上，就得到了平均毛管压力曲线。

按照上述步骤，对本文中测得的3组毛管压力曲线，拟合求得A、B、D和pcmin以及它们的平均值见表2。

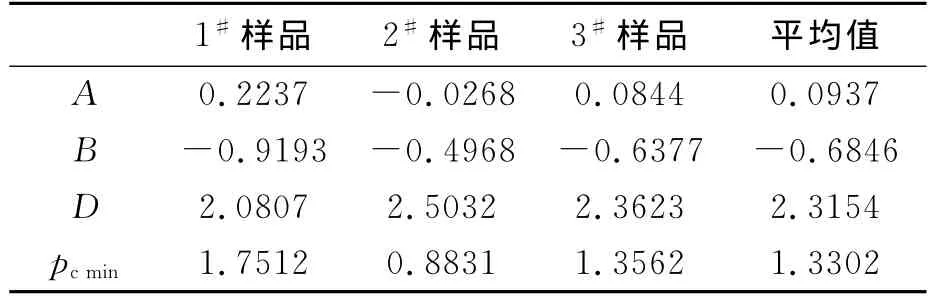
表2 3组毛管压力曲线求得的A，B，D和pc min以及它们的平均值Table 2 The calculated A，B，D，pc minand the average values

于是，得到平均毛管压力表达式为

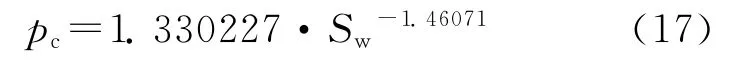
将平均含水饱和度代入方程（17），计算出平均毛管压力，并将所得到的数据画在pc－Sw坐标上，于是，得到一条平均毛管压力曲线（图4）。

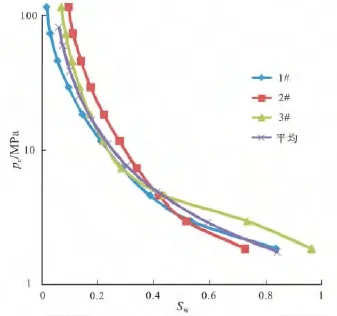
图4 平均毛管压力曲线Fig.4 Average capillary pressure curve

5 结论

a.本文利用分形理论证明了Lekia提出的观点：对于渗透率低的致密砂岩气藏，毛管压力与含水饱和度双对数曲线近似为一条直线段，可以按照线性拟合。而Corey等提出的毛管压力与归一化含水饱和度的线性拟合仅适用于渗透率较高的储层。

b.排驱压力与分形维数影响着毛管压力曲线的形态，排驱压力越小，毛管压力曲线越往下偏移，孔喉歪度越粗；分形维数越接近2，毛管压力平坦段越长，表明岩石孔喉的分选越好。

c.通过毛管压力模型，可以建立关于毛管压力与含水饱和度的数学关系式。利用毛管压力模型能够求取平均毛管压力曲线，方法简便，易实现。

［1］Brooks R H，Corey A T.Properties of porous materials affecting fluids flow［J］.Journal of Injection and Drainage Division，1966，No.IR2：61－88.

［2］Lekia S D L.A water-gas relative permeability relationship for tight gas sand reservoirs［J］.Journal of Energy Resources Technology，1990，112：239－245.

［3］Mandelbrot B B.The Fractal Geometry of Nature［M］.New York：W.H.Freeman and Company，1983.

［4］马新仿，张士诚，郎兆新.用分段回归方法计算孔隙结构的分形维数［J］.石油大学学报：自然科学版，2005，28（6）：54－56.Ma X F，Zhang S C，Lang Z X.Calculation of fractal dimension of pore structure by using subsection regression method［J］.Journal of the University of Petroleum，2005，28（6）：54－56.（In Chinese）

［5］Krohn C E.Fractal measurements of sandstone，shale and carbonate［J］.Geophys Res，1988，93（4）：3297－3305.

［6］Katz A J，Thompson A H.Fractal sandstone pores：implications for conductivity and formation［J］.Phys Rev Lett，1985，54（3）：1325－1328.

［7］Wells J D，Amaefule J O.Capillary pressure and permeability relationships in tight gas sands［C］//Proceedings of the 1985SPE/DOE Joint Symposium on Low Permeability Gas Reservoir.Denver：Science Petroleum Engineering，1985：85－95.

［8］贺承祖，华明琪.储层孔隙结构的分形几何描述［J］.石油与天然气地质，1998，19（1）：15－23.He C Z，Hua M Q.Fractal geometry description of reservoir pore structure［J］.Oil ＆ Gas Geology，1998，19（1）：15－23.（In Chinese）

［9］Giri A，Tarafdar S，Gouze P，etal.Fractal pore structure of sedimentary rocks：simulation in 2-d using a relaxed bidisperse ballistic deposition model［J］.Journal of Applied Geophysics，2012，87：40－45.

［10］杨宇，孙晗森，彭小东，等.煤层气储层结构分形特征定量研究［J］.特种油气藏，2013，20（1）：31－33.Yang Y，Sun H S，Peng X D.Quantitative study on fractal characteristics of the structure of CBM reservoir［J］.Special Oil and Gas Reservoirs，2013，20（1）：31－33.（In Chinese）

［11］缪志伟.一种计算平均毛管压力曲线的方法［J］.新疆石油地质，1997，18（1）：67－70.Miao Z W.A method for determining average capillary pressure curve［J］.Xinjiang Petroleum Geology，1997，18（1）：67－70.（In Chinese）