不确定环境下应急物资配送问题研究*
陈则辉,刘诚,吕品,刘叶飙
(1.南昌工学院经济管理学院,江西南昌330108;2.中南大学数学与统计学院,湖南长沙410075)
近年来,重大自然灾害事件频发,相关应急决策问题受到越来越多的关注[1-2]。应急物资配送作为应急救援过程中的一个重要环节,成为应急物流研究的重要课题。Gendreau等[3]考虑了受灾点位置不确定及受灾点的需求量是随机数的车辆路径问题,给出了求解该模型的禁忌搜索算法;Salmeron等[4]将多目标规划与随机规划结合运用到解决人道主义物流设施扩建、物资配送问题中;Changa等[5]研究了一个基于遗传算法的多目标应急物资调度模型的贪婪算法,该算法可根据需求点的需求动态调整配送计划,以减少资源浪费,缩短交付时间和降低运输成本;Novoa等[6]建立了随机需求下车辆路径模型,利用蒙特卡罗随机模拟算法将随机需求量转化为确定性需求量,并给出了该模型的近似动态规划算法;ZHANG[7]在不确定环境下建立了车辆路径问题的模型;杨菊花等[8]运用多式联运和路网的脆弱性理论,建立了应急物资全程调拔时运输方式和路径选择问题的综合模型;佟常青等[9]研究了城市交通背景下的军队应急物资配送路径优化选择问题,以军队应急物资配送的时效性和安全性特征作为评价指标,建立了评价备选路径的多目标决策模型;YANG等[10]针对应急车辆线路规划,建立了多目标数学规划模型,并给出了合理有效的求解算法;蔡鉴明等[11]将时效性和可靠性作为应急物流运输路径选择主要评价指标,构建了预测和评价应急物流运输路径的多目标决策模型;詹沙磊等[12]考虑了灾害预测准确性和物流成本效率之间的悖反关系,从多目标规划和随机规划的角度,建立了应急物资配送的多目标随机规划模型;陈森等[13]利用时延要素和物资要素之间的转换,同时考虑抢修毁损路段和车辆配送,实施路网结构、车辆路径联合优化,并求得了符合决策者意愿的配送体系,建立了该问题的联合优化模型;Ren等[14]在路网连通的不确定性条件下,建立了多种应急物资配送的多周期动态运输模型。以上文献大部分只是针对某一层面去考虑应急物资配送问题,如文献[6]只在需求为随机数的条件下考虑VRP,文献[14]只在路网不确定的条件下研究了应急物资配送问题。而在以往的应急物资配送问题研究中,对多个参数同为不确定数且同时以总时间满意度最大及系统运输总成本最低为目标的应急物资配送问题的研究比较少。本文针对受灾点的需求量、车辆从配送中心到受灾点的运行时间及单位运输成本为三角模糊数,建立了总的时间惩罚成本最小和系统总运输费用最省的双目标规划模型,给出了模型的有效解法。
1 问题的描述及模型的建立
1.1 问题的描述
设有一个应急配送中心O,拥有容量为q的车辆K辆,现有N个受灾地区向配送中心请求救灾物资配送,以1,2,…,N表示。本文将配送中心编号为0,各受灾点编号为1,2,…,N,受灾点及配送中心均已点i(i=1,2,…,N)表示,将这些点集记为:V={0,1,2,…,N}。已知第i个受灾点对于物资的需求量为(三角模糊数),且<q,否则对这个受灾点先进行整车配送,直到剩余的需求量小于车辆的最大容量;RTi表示车辆到达受灾点i的时刻,STi表示车辆在受灾地i的卸货时间;(三角模糊数)表示车辆由地点i行驶到地点j的时间;(三角模糊数)表示车辆从地点i行驶到地点 j的单位费用;dij(i,j∈V,且 i≠j)为地点i直接到达地点j的距离,且应急配送中心与受灾点及受灾点与受灾点之间都有线路相通,即为完全网络,车辆从配送中心出发,经过一系列受灾点后返回配送中心;ETi为受灾点i感觉到满意时所能接受的最长等待时间,LTi为受灾点i感觉到不满意时的最短等待时间,即应急物资在ETi之前送达受灾点i,受灾点i会感觉到满意;应急物资在(ETi,LTi]时间段内送达受灾点i,受灾点i感觉到的满意程度会逐渐降低;应急物资在LTi之后送达受灾点i,对受灾点i来说没有任何救援意义,其中ETi<LTi。为建立物资配送模型,定义如下变量:

时间在应急物流活动中的至关重要,为此,针对应急物流配送设定了2个救援时间分界点ETi和LTi,并针对时间分界点给出了符合应急物流活动的时间惩罚成本的函数:

式中:βi是时间敏感系数,决策者可根据受灾点i对时间要求的严格程度给出适当的值。
1.2 模型的建立
根据以上描述,问题是如何选择车辆运行路线使得总的时间惩罚成本最小和系统运输总费用最小。因此,建立以下模型:
模型(Ⅰ)

其中:目标函数(1)表示所有受灾点时间满意度之和;目标函数(2)表示运输总费用;约束条件(3)表示车辆的任务量必须小于车辆的容量;约束条件(4)表示应急配送中心车辆总数;约束条件(5)表示每一个受灾点的任务只能由1辆车完成;约束条件(6)和(7)表示到达和离开某一个受灾点的车辆有且只有1辆;约束条件(8)为支线消去约束,为了避免出现孤立圈;约束条件(9)表示每辆车从配送中心出发又回到配送中心;约束条件(10)表示到达受灾点j的时间要不早于到达受灾点i,为受灾点i的服务时间与受灾点i到受灾点j的行驶时间之和;约束条件(11)为0-1约束。
2 模型转化及算法设计
2.1 模型转化
模型(Ι)是一个模糊规划模型,为了求解该模型,需要将其转化为确定性模型。
(1)将模型(Ι)中三角模糊参数转化为确定性参 数,由 Pishvaee[15],定 义 三 角 模 糊 数的隶属函数:

(2)结合三角模糊数的性质,给出以下随机模拟算法:
Step3:重复step1和step2 M次(M为一个较大的正整数),取σ的平均值即可等价于模糊数。
模型(Ⅱ)

其他约束条件与模型(Ι)相同。
2.2 算法设计
模型(Ⅱ)是一个NP-难问题,首先将模型转化为单目标规划模型。由于2个目标函数的量纲相同,可将双目标进行线性加权转化为单目标,于是模型(Ⅱ)中双目标函数可转化为:
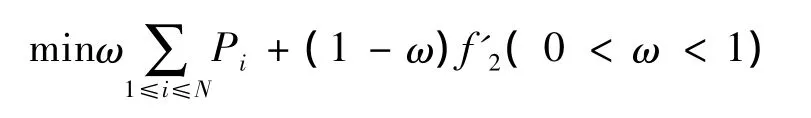
在以上基础上,给出以下C-W节约算法:
Step 1:求配送中心到各受灾点、受灾点到受灾点的最短距离;
Step 2:根据节约量公式 s1(i,j)=c0id0i+cj0dj0-cijdij,计算连接点对后运输成本节约量值,令M1={s1(i,j)}。本文模型考虑车辆最后是空载回到配送中心的情况,所以运输成本不是对称成本,s1(j,i)≠s1(i,j)在计算节约量时还要算 s1(j,i)=c0jd0j+ci0di0-cjidij;
Step 3:将配送中心到各受灾点的模糊运行时间转化为时间平均数,根据时间惩罚成本函数,计算出

Step 4:计算时间成本节约量,连接受灾点i和j后,车辆到达受灾点j的时间为STi,计算Pi,从而根据节约量的计算公式可得:s2(i,j)=P0i+Poj- P0i- Pj=Poj- Pj,通过此式可以计算出受灾点对连接后的时间满意度惩罚成本节约量;
Step 5:根据公式 s(i,j)= ωs1(i,j)+(1 -ω)s2(i,j),计算总的节约量 s(i,j),记M={s(i,j)|s(i,j)≥ 0};
Step 6:在M中按照s(i,j)从大到小进行排序,逐项检查对应的受灾点之间的连接,在M中取s(i,j)最大的受灾点对,判断这2个受灾点所需货物之和是否超过车辆的最大载重量,若超过,则这2个受灾点不能在同一条配送线路上;若不超过,则连接i和j,形成线路0→i→j→0,并在M中删除以i为前的受灾点对(i,*)和以j为后的受灾点对(*,j);
Step 7:在M的剩余受灾点对中取s(i,j)最大的受灾点对:
(1)如果该点对中的受灾点均不在已构成的线路上,则重复Step7的操作;
(2)如果该点对中的前外受灾点是已构成的线路上的后外受灾点,即出现受灾点对(j,k)时,则形成线路0→i→j→k→0,判断该线路中车辆是否超载,若超载则受灾点j和k不予连接,并在M中删除s(j,k),若没有超载,准予连接受灾点j和k;
(3)如果该受灾点对中的后外点是已构成的线路上的后外受灾点,即出现点对(u,i)时,则形成线路0→u→i→j→0,判断该线路中车辆是否超载,若超载则受灾点u和受灾点i不予连接,并在M中删除s(u,i),若没有超载,准予连接受灾点u和受灾点i;
Step 8:在M中剩下的受灾点对中选择节约量最大的受灾点对,重复Step 6-Step 7,当产生出一条线路时,在M中删除所有与该线路上受灾点的相关连接;直至M为空集。
3 算例
假设某次自然灾害中,某个配送中心需向8个受灾点运送应急救灾物资,具体数据见表1~表5(三角模糊数和已根据随机模拟算法转化为确定数和)。

表1 受灾点的相关数据Table 1 Relevant data of each disaster area

表2 配送中心到受灾点、受灾点到受灾点的运行时间Table 2 Running time from distribution center to each disaster area and the running time from disaster area to disaster area

表3 时间敏感系数Table 3 Time sensitive coefficient

表4 配送中心到受灾点、受灾点到受灾点的运费Table 4 Transportation cost from distribution center to each disaster area and transportation cost from disaster area to disaster area

表5 配送中心到受灾点、受灾点到受灾点的最短距离Table 5 Minimum distance from distribution center to each disaster area and minimum distance from disaster area to disaster area
由于本文考虑的是应急物资配送问题,故时间满意度应重点考虑,故取ω=0.8,另取P=10,K=4,q=12,用随机模拟算法将以上模糊数转化为确定数,再运用以上C-W算法可得如下结果:
(1)受灾点对连接的距离成本节约量s1(i,j)按从大到小顺序排列如表6所示。

表6 运输成本节约量Table 6 Savings of transportation cost
(2)受灾点对连接的时间惩罚成本节约量s2(i,j)按从大到小顺序排列如表7所示。

表7 时间惩罚成本节约量Table 7 Savings of time penalty cost
(3)当ω=0.8时,受灾点对连接的加权后总成本节约量s(i,j)按从大到小顺序排列如表8所示。
(4)由表8可得以下车辆路径,见图1。

图1 车辆路径运行图Fig.1 Vehicles running diagram
此时节约总量为351.685千元。
由于决策者的偏好或者具体情况的不同,当ω取值不同时,决策方案也不同,以下列举出几种ω的值,所得出的结果图2所示。

图2 不同权重ω所对应的节约量Fig.2 Savings corresponding to different weights ω
由图2可知:随着权重值ω的增加,物流配送系统的总节约量总体趋势是越来越小,故决策者应根据实际灾情,选择合适的权重值,在保证合理时间满意度的前提下,适当降低物流系统成本。
4 结论
(1)假定受灾点的需求量、车辆从配送中心到受灾点的运行时间及单位成本为三角模糊数的应急物资配送问题,建立了系统总费用最小和总的时间惩罚成本最小的双目标规划模型。
(2)通过算法和算例分析表明,最优的车辆路径的决策方案与权重值ω关系密切,故决策者在决策时应根据实际情况选择合适的权重值ω,这对应急物流配送问题有一定的借鉴意义。
(3)本文只考虑了单个配送中心、单物资配送问题以及将不确定因素定位在三角模糊数,而在现实的应急物流配送中往往是多配送中心、多种应急物资以及多种不确定数(模糊数、随机数等),这将是应急物资配送下一步的研究内容。
[1]Sheu J B.Dynamic material-demand management for emergency logistics operations under large-scale disasters[J].Transportation Research Part E,2010,46(1):1 -17.
[2]HU Zhihua.A container multimodal transportation scheduling approach based on immune affinity model for emergency material[J].Expert Systems with Applications,2011,38(3):2632 -2639.
[3]Salmeron J,Apte A.Stochastic optimization for natural disaster asset prepositioning[J].Production and Operations Management,2010,19(5):561 - 574.
[4]Genderau M,Gilbert L.A tabu search heuristic for the vehicle routing problem with stochastic demands and customers[J].Operations Research,1996,4(23):469 -477.
[5]Changa F S,Wua J S,Leea C N,et al.Greedy-search-based multi-objective genetic algorithm for emergency logistics scheduling[J].Expert Systems with Applications,2014,41(6):2947 -2956.
[6]Novoa C,Robert S.An approximate dynamic programming approach for the vehicle routing problem with stochastic demands[J].European Journal of Operational Research,2009,196(2):509-515.
[7]ZHANG Jing.Control of the supply chain optimization with vehicle scheduling of logistics under uncertain systems[J].Procedia Environmental Sciences,2012,12(Part B):1440-1445.
[8]杨菊花,朱昌锋,田志强.基于蚁群算法的应急物资运输路径优化[J].铁道科学与工程学报,2012,9(6):90-94.
YANG Juhua,ZHU Changfeng,TIAN Zhiqiang.Trans-port path optimization for emergency material based on ant colony algorithm[J].Journal of Railway Science and Engineering,2012,9(6):90 -94.
[9]佟常青,王景国,陈博文.军队应急物资配送备选路径优化多目标规划模型研究[J].物流技术,2010,29(2):206-208.
TONG Changqing,WANG Jingguo,CHEN Bowen.A multi-objective programming model of routing optimization for military emergency material distribution[J].Logistics Technology,2010,29(2):206 -208.
[10]LIU Yang,YUN Meiping,PENG Guoxiong.A multiobjective programming model of route choice of emergency vehicles before travel[J].Journal of Highway and Transportation Research and Development,2009,26(8):135-139.
[11]蔡鉴明,李夏苗,杨光华.基于时变性和可靠性的地震灾害应急物流运输路径选择[J].铁道科学与工程学报,2011,8(5):101 -106.
CAI Jianming,LI Xiamiao,YANG Guanghua.The routing problem for emergency logistics considering the reliability and time-varying in the earthquake disasters[J].Journal of Railway Science and Engineering,2011,8(5):101 -106.
[12]詹沙磊,刘南.基于灾情信息更新的应急物资配送多目标随机规划模型[J].系统工程理论与实践,2013,33(1):159-166.
ZHAN Shalei,LIU Nan.Multi - objective stochastic programming model for material allocation based on disaster scenario information updates[J].Systems Engineering-Theory& Practice,2013,33(1):159-166.
[13]陈森,姜江,陈英武.未定路网结构情况下应急物资车辆配送问题模型与应用[J].系统工程理论与实践,2011,31(5):907 -913.
CHEN Sen,JIANG Jiang,CHEN Yingwu.Emergency logistics distribution problem model under uncertain roadway network structure and its application[J].Systems Engineering-Theory& Practice,2011,31(5):907-913.
[14]Ren Xide,Zhu Jianming,Huang Jun.Multi- period dynamic model for emergency resource dispatching problem in uncertain traffic network systems[J].Engineering Procedia,2012,22(5):37 -42.
[15]Pishvaee M S,Torabi S A.A possibilistic programming approach for closed-loop supply chain network design under uncertainty[J].Fuzzy Sets and Systems,2010,161(20):2668-2683.

