RBF 与BP 网络在模式分类领域内的对比研究

丁 硕，常晓恒，巫庆辉

（渤海大学工学院，辽宁锦州，121013）

反向传播神经网络（Back Propagation Neural Networks, BPNN）存在收敛速度慢、训练时间长、目标函数易陷入局部最小值等缺点。径向基函数神经网络（Radial Basis Function Neural Networks, RBFNN) 是一种局部逼近的神经网络，由于RBFNN 的激活函数采用径向对称的核函数，当输入样本传输到隐含层单元空间时，这组核函数构成了输入样本的一组基，当输入信号靠近核函数的中央范围时，隐含层节点将产生较大的输出，所以RBFNN 具有学习速度快、逼近精度高的优点，能较好地克服标准BPNN 的训练时间长及计算复杂度高等缺点。本文基于RBFNN 和标准BPNN 的分别构建了分类模型，通过仿真实验，对2 个模型的分类性能进行对比。仿真结果表明，在对二维数据进行模式分类时，基于RBFNN 的分类模型更具优势，更适合于解决模式分类问题。

1 RBFNN 的结构与算法

RBFNN 由输入层、隐含层和输出层组成的三层前向网络。输入层由信号源节点组成；隐含层神经元采用径向基函数作为变换函数，径向基函数常用高斯函数，设Xp为输入样本，为欧式范数，c 为高斯函数的中心， 为高斯函数的方差，则网络的输出如式(1)所示，其中wij为隐含层到输出层的连接权值，h 为隐含层神经元数目，yj为与输入样本对应的第j个输出神经元的实际输出。基函数的方差如式(2)所示，其中d 为样本的期望输出值。

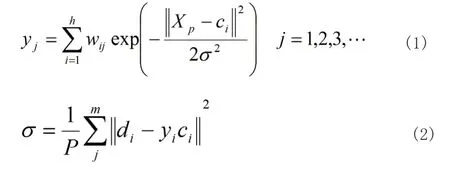
2 BPNN 的结构与算法

BPNN 是一种单向传播的多层前向网络，BPNN 通过对输入节点与隐层节点间的网络权值wij、隐层节点与输出节点间的网络权值Tli及阈值 的调整，使误差函数沿梯度方向下降。设BPNN 的输入节点为xj、隐层节点为yi、输出节点为Ol、输出节点的期望输出为tl,则BPNN 隐层节点的输出计算方法如式(3)所示，输出节点的计算方法如式(4)所示。

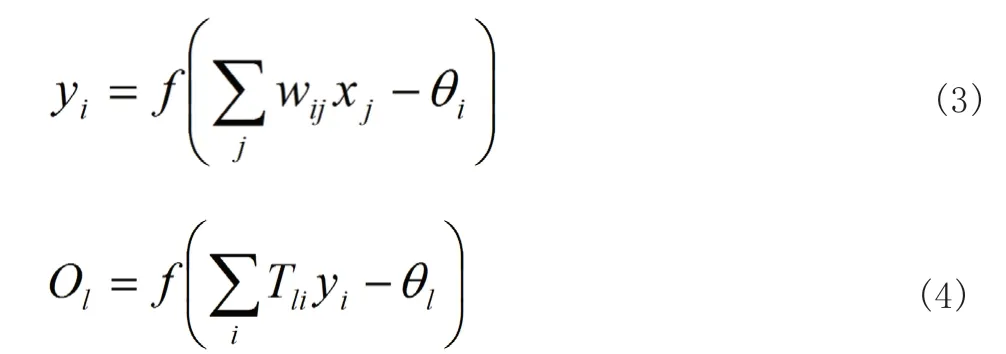
3 仿真实验

3.1 RBFNN 与BPNN 分类模型的建立

利用RBFNN 和标准BPNN 分类模型对图1 所示的30 个样本二维向量的模式进行分类。在对样本二维向量的模式进行分类实验时，首先对向量的模式进行编码，即网络的输出分别用一组二进制代码来表示对应向量的模式，本文分别用(0 0 0 0 1)表示第1 类模式；(0 0 0 1 0)表示第2 类模式；(0 0 1 0 0)表示第3 类模式；(0 1 0 0 0)表示第4 类模式；(1 0 0 0 0)表示第5 类模式。本文选用高斯函数作为RBFNN 隐含层神经元的径向基函数；RBFNN 的中心在输入样本中随机选取，参数C 由相邻样本数据的最大距离确定，经过反复实验，最终确定当C=0.035 时，网络分类性能最好。对于标准BPNN而言，可以确定网络输入层为30 个神经元，输出层有5 个神经元；训练函数采用traingd；隐含层神经元数为25 时，可以满足分类要求，学习率为0.1；最大训练次数设为30000；目标精度设为0.001。

3.2 RBFNN 与标准BPNN 分类模型对训练样本的分类结果

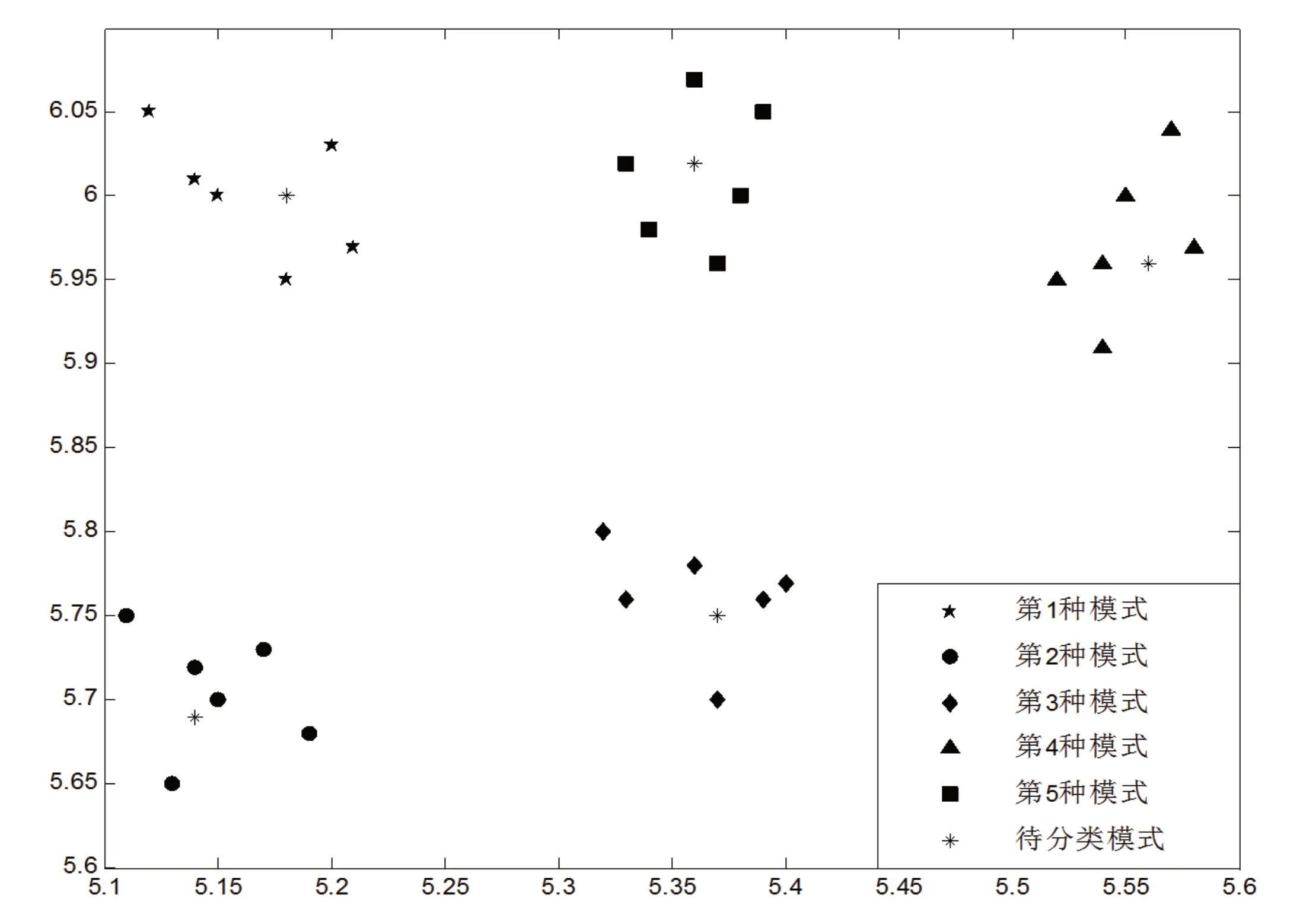
图1 样本向量与测试向量分布

在目标精度设置为0.001、训练样本数目相等的条件下，标准BPNN 分类模型需要23507 步才能达到目标精度，均方误差为0.000999971，勉强达到目标精度要求；RBFNN分类模型只需要28 步就可以达到目标精度，均方误差仅为0.000515480，远远高于目标精度要求。可以得出结论，对于训练样本集而言，只要训练步数设置足够大，2 种分类模型都能在预设的训练步数范围内完成对训练样本的模式分类任务，但相比之下，RBFNN 的收敛时间明显比标准BPNN 少，均方误差也远小于标准BPNN，即RBFNN 分类模型对于训练样本分类的准确性和分类精度更高，收敛速度更快。

3.3 RBFNN 与标准BPNN 分类模型的泛化能力测试

利用2 种分类模型对5 个不同类别向量作为测试向量进行分类。如图1 所示，(5.18,6.00) 属于第1 类，(5.14,5.69) 属于第2 类，(5.37,5.75) 属于第3 类，(5.56,5.96) 属于第4 类，(5.36,6.02)属于第5 类。RBFNN 和标准BPNN 对测试样本的分类结果如表1 所示，可以看出，标准BPNN 分类模型的最大绝对误差为-0.3427，RBFNN 分类模型的最大绝对误差仅为-0.0968。可以得出结论，对于测试样本集而言，RBFNN的分类结果更为精确，分类性能更优；标准BPNN 的分类结果误差较大，分类性能较差。

4 结论

本文分别构建了RBFNN 与标准BPNN 分类模型，并对输入的二维向量模式进行分类实验。仿真结果表明：只要训练步数设置足够大，RBFNN 和标准BPNN 都能对训练样本和测试样本实现正确分类,但标准BPNN 训练时间较长，并且要经过多次训练才能得到较好结果，而RBFNN 训练时间很短，分类精度也明显高于标准BPNN, 分类性能明显优于标准BPNN。

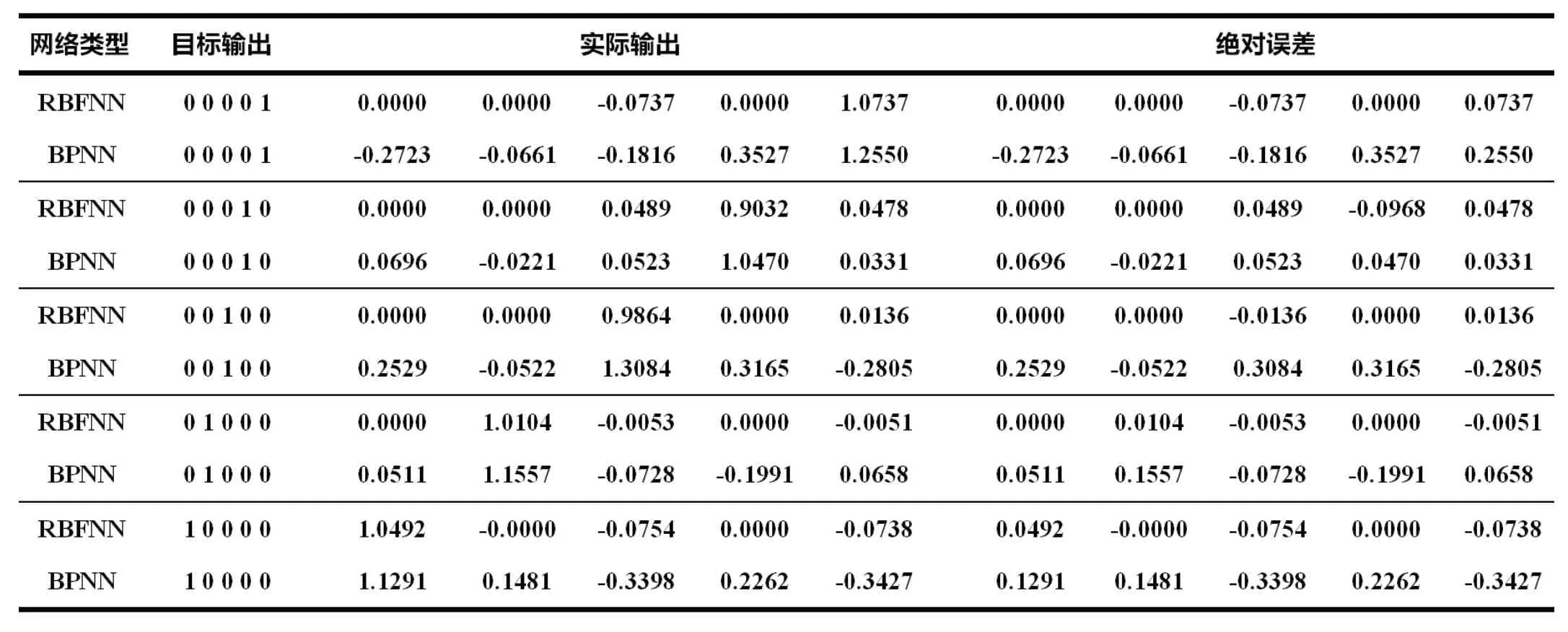
表1 RBFNN 和标准BPNN 对测试样本的分类结果对比

[1] 余妹兰，匡芳君.BP 神经网络学习算法的改进及应用[J]. 沈阳农业大学学报,2011,42 (3) :382-384.

[2] 丁硕，巫庆辉.基于改进BP 神经网络的函数逼近性能对比研究[J].计算机与现代化， 2012，(11)：10-13

[3] 丁硕，常晓恒，巫庆辉.基于Gaussian 型RBF 神经网络的一元函数逼近性能研究[J].渤海大学学报(自然科学版)， 2013，34(3)：300-304

[4] 刘永，张立毅.BP 和RBF 神经网络的实现及其性能比较[J]. 电子测量技术，2007，30（4）：77-80

[5] DING Shuo,CHANG Xiao-heng,WU Qing-hui.Fault Diagnosis of Induction Motors Based on RBF Neural Network [J].Applied Mechanics and Materials,2014. (462-463):85-88

[6] 刘天舒.BP 神经网络的改进研究及应用[D].哈尔滨：东北林业大学, 2011.