修正的演化少数者博弈在NW 小世界网络上的模仿效应分析
刘英明,全宏俊
(华南理工大学物理系,广东广州,510641)
1 模型描述
首先构造一个NW 小世界网络,开始每个节点与其左右对称的相邻2k 个节点相连构成规则网络,然后,每个节点都以一定的概率ps与相邻2k 节点外的其他一个节点相连,并且不能与自己相连。每个节点代表一个经纪人,相连的节点代表经纪人之间为邻居。每个经纪人都有一个策略、一个概率值p 和相同m 的历史记忆量:μ(t)={b(t-m),…,b(t-2),b(t-1)},其中,b(t)=“0”或“1”。所有经纪人做出选择后处于少数方的经纪人获胜,并且其得分加1,处于多数方的经纪人得分减1。博弈开始前,每个经纪人从策略库中随机抽取一个策略作为自己的策略,并且均匀随机分配一个概率策略p。博弈时,每个经纪人根据历史记录和策略来预测下一步的获胜方;并且以自己的概率p 决定去自己策略的预测方,以1p 去策略预测方的相反方。相邻经纪人之间的得分与概率p 是共享的,因此每个经纪人都知道自己邻居的得分与概率。当经纪人的得分低于某一值d(d<0)时,经纪人以其邻居中得分最高的经纪人的概率为中心,2dp 为宽度,均匀随机重新选择一个新的概率p,若得分最高的邻居有2 个及以上,则从中随机选择一个;若自己得分最高则以自己为中心,2dp 为宽度,重新选择。模型中采用反射边界条件保证新概率p 在[0,1]之间。相比于Quan H.J等人提出的博弈模型,本文模型中每个经纪人多了一个从策略库中随机选择的策略。
这一模型的系统标准差可以表示为:
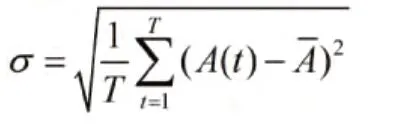
其中A(t)表示t 时步选择A 方的人数, 表示T 时步内选择A 方的人数的平均值。
2 结果与讨论
考虑N=1001,d= 4,k=5 的系统。图1 ~ 4 和图6 中,每个数据点都是50 次取平均值,每次都是运行107后,对106时步的结果做统计平均。图1 给出了m=3,2dp=0.1 时,不同重连概率ps下的经纪人的概率分布图,可以看出p 在p=0 和p=1 处也出现了类似于EMG 的自相分离现象,。
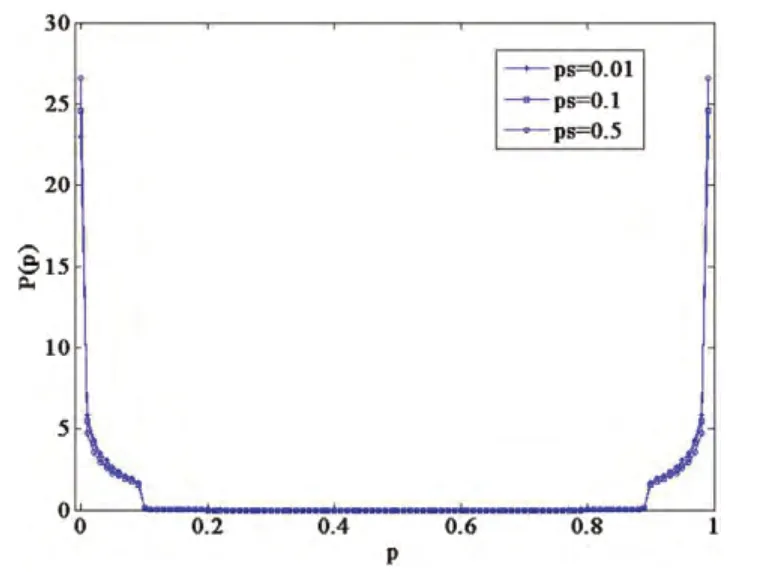
图1 m=3 时 不同重连概率ps 下的概率p 分布P(p)
图2 给出了不同m 下的概率p 分布,可以看出p 分布P(p)与m 有着密切的关系;在m 小时p 分布在p~0 和p~1 处密集,中间段最小,自相分离程度很高;随着m 的增大,P(p)变得平滑,自相分离程度越来越低。原因是,在m 很小的时,,策略库中的所有策略都被经纪人所用,并且所有的策略都均匀分布在经纪人当中,再加上每个经纪人都只有一个策略,使得人群-反人群效应达到最优,因此出现的自分离程度最大;随着m 的增大,策略库中的策略只有一部分策略被经纪人所有,策略与策略的反策略不能够同m 很小的时候一样都被均匀的利用,人群-反人群效应变小,自分离程度也就减小;当m 增大到 ,此时策略库中只有很少的一部分策略被经纪人所用,策略与策略的反策略被同时使用的几率减小到很小,人群-反人群效应最小,进入了随机选择状态。
图3 给出了不同ps 下, 与m 的关系,可以看出,在m=1 时,系统方差最小;随着m 的增大,系统方差逐渐增大;当m 增加到极限时,系统方差趋于随机选择。原因见对图2 的分析。从图3 还可以看出,ps=0.5 的系统方差要比ps=0.1 的系统方差要小,为了解释这一原因,图4 给出了 /N 与集聚系数C 的关系,发现随着集聚系数的增加 /N 不断减小,且减小的幅度不断增加,而ps的增加将引起C 的减小,(见图5),所以重连概率越大,小世界网络的聚焦系数越小,集团化程度越低,系统方差也就越大。图5 给出了给出了WS 小世界网络和NW 小世界网络的集聚系数与ps的关系,可以看出,在Ps较大时,NW 的集聚系数要大于WS,说明此时NW 的集聚度较WS 要高。
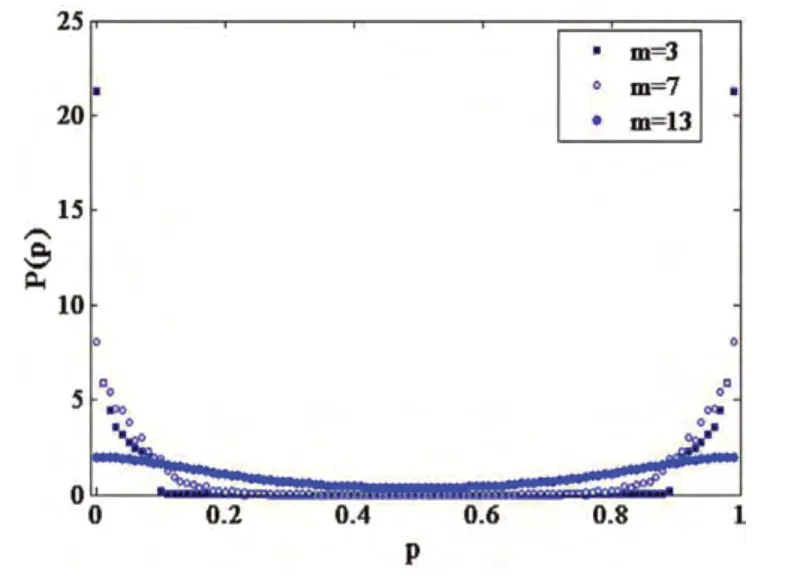
图2 不同m 下的概率分布P(p)
图6 给出了ps=0.1 时,这本文模型与“WS 小世界网络上修正的演化少数者博弈模型”(WSMEMG)的 /N 与m 的关系对比。可以看出,在相同重连概率下,本文模型的系统方差相比于WSMEMG 模型的方差要小,原因是ps=0.1 时,NW 小世界网络的集聚系数相比于WS 小世界网络要大;在ps=0.1 时NW 小世界网络结构的聚焦系数 ,WS 小世界网络的集聚系数 ;集聚系数的大表明经纪人之间通过模仿交流所获得信息增多,从而系统方差减小。
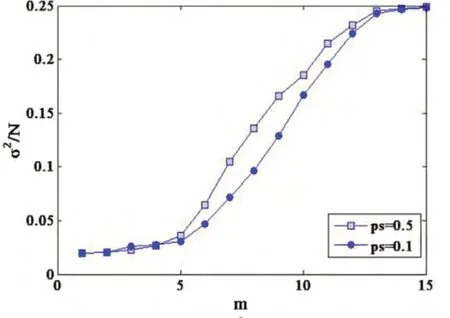
图3 不同ps 下 /N 与m 的关系
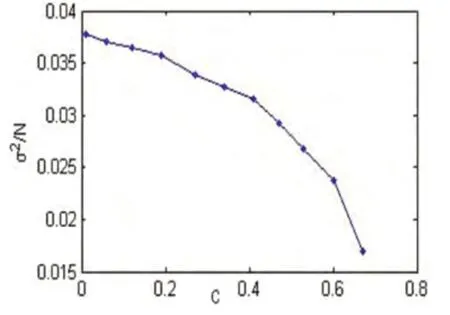
图4 /N 与集聚系数C 的关系
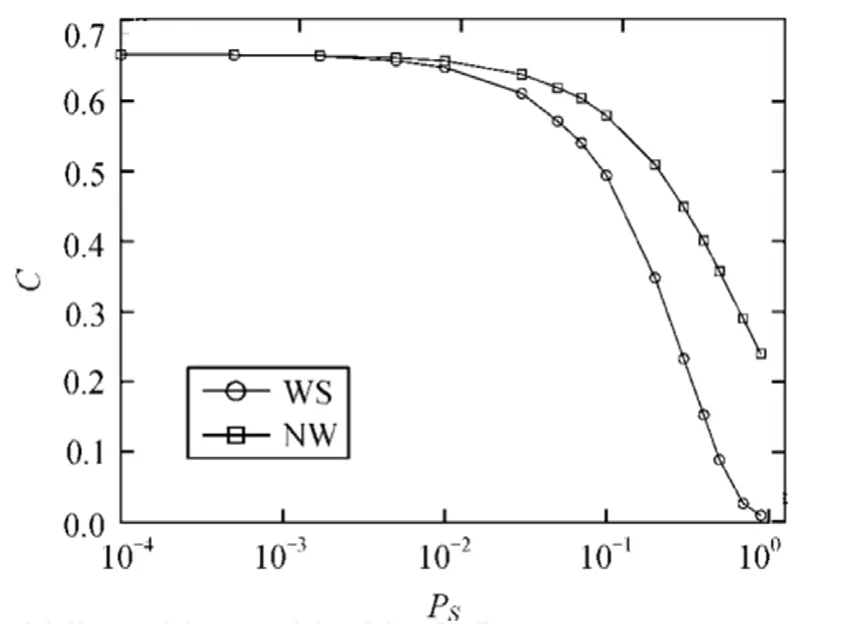
图5 NW 和WS 两种小世界网络的集聚系数与ps 的关系
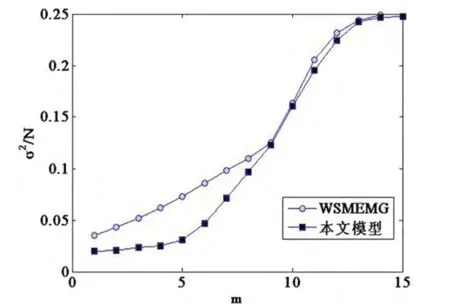
图6 本文模型与WSMEMG 模型的 /N 随m 的变化关系的对比
3 结论
本节主要研究了NW 小世界网络上修正的演化少数者博弈的模仿效应,发现了这一模型的系统同样出现了经纪人的自组织分离现象;并且与“WS 小世界网络上修正的演化少数者博弈的模仿效应”进行了对比分析,由于NW 小世界网络的集聚系数较WS 小世界网络的集聚系数大,集团化程度高,系统方差也就要小。
[1] Newman M.E.J,Watts D.J.Renormalization group analysis of the small-word network model [J].Phys.Lett.A,1999,263:341-346
[2] Challet D,Zhang Y.C.Emergence of cooperation and organization in an evolutionary game[J].Physica A,1997,246:407-418
[3] Lo T.S,Hui P.M,Johnson N.F.Theory of the evolutionary minority game[J].Phys.Rev. E,2000,62:4393-4396
[4] Shang L.H,Wang X.F.Evolutionary minority game on complex networks [J].Physica A,2007,377:616-624
[5] Quan H J et al.Cooperation in the mixed population minority game with imitation [J].Chin.Phys.Lett, 2001,18:1156-1158

