基于非线性组合模型对石油价格的预测

赵 庆

（1.东北财经大学 金融学院，辽宁 大连116025；2.辽宁对外经贸学院 财政金融系，辽宁 大连116025）

0 引言

石油作为经济的“血液”，其在经济建设中所起的重要作用不言而喻，同时对金融市场也产生显著影响。金洪飞和金荤研究表明，国际石油价格对中国能源类股票收益具有显著正向影响，对建筑和材料等行业具有显著的负向影响［1］。Miller和Ratti发现，OECD六国1999年后国际原油价格对于股票市场存在长期显著负向影响［2］。彭民和孙彦彬发现，原油期货价格的涨跌与美元指数之间存在较长期的负相关关系［3］。鉴于预测石油价格对于生产活动及金融活动的重要性，国内外对石油价格预测模型进行了大量研究，覃丽萍等基于支持度计数矩阵和事务数据库布尔矩阵的新算法，挖掘石油期货价格历史数据中的频繁项集，根据给定的最小支持度和最小置信度从挖掘结果中产生关联规则，对关联规则在石油期货价格预测中的应用进行了探索［4］。陈卫东等基于复杂网络的动力学拓扑性质，构建原油价格有向加权波动网络，用复杂网络拓扑结构记录原油价格波动周涨落的信息，计算网络的度与度分布、聚类系数、最短路径长度等动力学统计量［5］。王洲和马燕林在非线性系统及复杂性理论框架内，采用相空间重构技术，提取描述吸引子特征量参数，定量地证明石油价格演化过程具有混沌特性，并采用混沌时间序列预测法预测石油价格走势［6］。孟刚等利用分形理论和国际石油价格建立预测模型［7］。胡国松和冯雪梅分析影响国际石油价格的长期影响因素和短期影响因素，应用灰色预测理论GM（1，1）模型推导出了国际油价的预测模型［8］。井霞霞等通过分数差分消除了WTI现货价格序列中的长记忆性，得到一条短记忆序列，然后，利用部分线性自回归模型对其进行建模［9］。梁强等将小波方法引入到油价长期趋势的预测中，利用小波多尺度分析的功能，提出了一种可以较为准确地根据油价时序列预测其未来长期走势的方法［10］。Ye等采用3－D图形方法，通过图形分析原油价格、存量及超额生产能力，兼及OPEC政策等因素建立石油需求与供给关系预测石油价格［11］。Wang等基于Hubbert模型和广义翁氏预测模型（Generalized Weng mode）预测世界原油产量［12］。Guo等将支持向量机和遗传算法结合，采用一种智能数据挖掘技术（GA－SVM）模型预测原油价格［13］。李红星将基于统计学理论的正则化最小二乘回归用到石油价格预测，得到较好预测结果［14］。Wang等集成了文本挖掘、计量经济学和智能技术，建立了TEI＠I方法［15］。Xie等采用支持向量机（SVM）对石油价格进行预测，并提出将SVM方法集成到TEI＠I方法中，取得了较好结果［16］。秦鹏和缪柏其使用拟合期内的样本，在不同准则下选取有限个不同参数的EWMA的非线性组合，基于广义指数预报因子模型预测石油价格［17］。赵庆和王志强运用混合模型对上海黄金交易所现货黄金AU99.99日收盘价格进行了预测［18］。

本文提出一种新的中期预测模型，利用HP滤波将部分石油价格序列分解为趋势要素序列和波动周期序列，然后针对趋势要素序列的性质建立自回归模型（AR）进行拟合和预测，使用石油价格序列与趋势要素序列预测值之差即随机周期波动序列建立ARMA模型拟合和预测，然后将趋势要素序列预测值与随机周期波动序列预测值之和作为预测值与剩余部分原石油价格序列进行预测值检验评价模型，同时将该模型与其它模型进行比较，中期预测精度高于其它模型，对于预测石油价格具有实际指导意义。

1 实证分析

1.1 数据选取

国际原油交易的三大基准原油 WTI，Brent和Dubai，它们之间的价格对比是决定全球原油价格走向的主要因素。本文采用2003年8月1日－2013年4月19日WTI现货价格周数据，共计508个数据的前456个数据进行建模，后52个数据用于预测检验。数据来源于美国能源情报署网站。

1.2 HP滤波对原始序列G分解

通过HP滤波选取λ＝100将原始时间序列G分解成趋势项序列T和周期波动项序列Y，得到的分解结果如图1所示。

从图1中可以看出，本文所选取的石油价格序列经历了一个较大的波动趋势，采用该时间段建模对模型的要求很高，也反映出该方法的适用性较强，同时还可以看出趋势序列T可以较好地反映出原序列的变化趋势，基本与原序列完全拟合，周期序列Y可以反映出原序列的波动情况。

图1 HP滤波分解图

1.3 趋势要素拟合和预测

在对趋势要素序列T使用自回归模型进行分析之前，首先，应该对该序列做平稳性检验，如果是非平稳的实际序列，要考虑对它进行平稳化处理后才能建立自回归模型。我们对趋势要素序列T进行单位根检验，结果ADF＝－3.427 78，小于5%显著水平临界值，所以趋势要素序列T在5%显著水平下是平稳序列。其次，对趋势要素序列进行自相关检验，发现趋势要素T的自相关系数是拖尾的，偏自相关系数在5阶截尾。同时根据AIC，SC最小准则来确定模型的阶数，以前456个数据为建模数据，经过多次拟合对趋势要素T建立AR（5）模型，模型估计参数如表1所示。其拟合系数为R2＝0.999 999，拟合效果非常好。

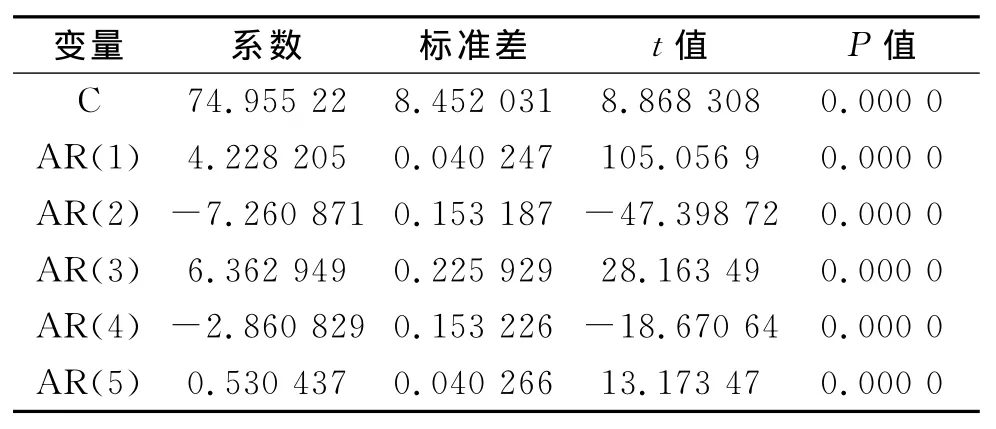
表1 自回归模型回归参数

通过AR（5）模型采用静态预测方法对样本外的52个数据进行预测，预测效果如图2所示。由图2可知，趋势序列预测效果非常好，趋势序列与预测序列几近完全拟合。然后通过Y0＝G－TF得到回归模型未预测的带有周期的随机波动序列Y0，建立模型对Y0进行拟合和预测。

1.4 周期随机波动序列Y0拟合和预测

同样首先对周期随机波动序列Y0进行单位根检验，通过检验得到ADF＝－10.959 65，小于1%检验水平的临界值，所以周期随机波动序列Y0是平稳序列。然后对周期随机波动序列Y0进行序列相关检验，得知其存在自相关和偏自相关。综上所述，周期随机波动序列Y0为平稳序列，但是存在自相关，因此可建立自回归移动平均模型（ARMA模型）。根据赤池信息量准则和施瓦茨准则进行多次尝试来确定模型的阶数，最后确定为ARMA（2，1），由于常数项C不显著（t值为0.017 690），故剔除常数项，并且拟合系数有所提高。详见表2。

图2 趋势要素T样本外预测

表2 自回归模型回归参数

同样在模型ARMA（2，1）的基础上采用静态预测方法对样本外的52个数据进行预测记为Y0F。

1.5 模型预测效果检验

将趋势要素序列T的预测值TF与周期随机波动序列Y0的预测值Y0F相加，作为原石油价格序列G的预测值GF，即GF＝TF＋Y0F，通过预测序列GF与原石油价格序列G比较，检验预测效果。

如图3所示，石油价格预测值GF能反映出原序列G的变化趋势。同时，为与其他模型比较预测结果，本文将文献［10］和［14］－［17］模型转换为中期预测范围，如表3所示。采用RMSE作为评价预测准确度指标：RMSE＝－］1／2。

图3 石油价格预测值GF与原序列G比较

通过表3可以看出，本文所提出的中期预测模型HP滤波－AR－ARMA模型能够精确地拟合并预测石油价格，预测精度明显高于其他模型，这对于石油价格预测具有实际指导意义。

表3 原油预测价格预测结果

2 结论

本文针对石油价格预测提出一种新的预测方法。首先使用HP滤波将原序列G分解成两部分周期性波动序列T和趋势要素序列Y；其次，针对序列不同的性质，建立不同模型拟合预测，对所选石油价格的趋势要素T根据序列性质，建立向量自回归拟合预测，预测值TF；然后计算随机周期波动序列Y0＝G－TF，对随机周期性波动序列要素建立ARMA模型拟合预测；最后将趋势要素序列预测值和随机周期性波动要素序列预测值进行相加，得到石油价格G预测序列GF，同时与原序列进行比较评价。本文所选取的模型能精确拟合并预测石油价格，在预测精度上相比较以前文献所选取的模型均有提高，效果很好，并且建模方法相比以前文献更加简单易用，便于推广。

［1］ 金洪飞，金荤.国际石油价格对中国股票市场的影响——基于行业数据的经验分析［J］.金融研究，2010，29（2）：173－187.

［2］ Miller J I，Ratti R A.Crude oil and stock markets：Stability，instability，and bubbles［J］.Energy Economics，2009，31（4）：559－568.

［3］ 彭民，孙彦彬.国际石油期货价格与美元指数动态关系的实证研究［J］.中国石油大学学报：社会科学版，2009，25（3）：1－4.

［4］ 覃丽萍，白玫，王海军，等.关联规则及其在石油期货价格预测中的应用研究［J］.数学的实践与认识，2009，39（1）：67－71.

［5］ 陈卫东，徐华，郭琦.国际石油价格复杂网络的动力学拓扑性质［J］.物理学报，2010，59（7）：4514－4522.

［6］ 王洲，马燕林.国际石油价格时间序列的混沌分析与预测［J］.资源科学，2008（12）：1791－1795.

［7］ 孟刚，唐雄，张意翔.国际石油市场的分形特征与价格突变分析［J］.统计与决策，2006，30（12）：53－54.

［8］ 胡国松，冯雪梅.基于灰色系统理论的国际石油价格预测方法［J］.中外能源，2010，15（12）：18－20.

［9］ 井霞霞，张德生，张延利，等.考虑外生变量的基于分数差分的石油价格部分线性自回归预测模型［J］.山西大学学报：自然科学版，2012，35（4）：620－625.

［10］ 梁强，范英，魏一鸣.基于小波分析的石油价格长期趋势预测方法及其实证研究［J］.中国管理科学，2005，13（2）：30－36.

［11］ Ye M，Zyren J，Blumberg C J，et al.A short－run crude oil price forecast model with Ratchet effect［J］.Atlantic Economic Journal，2009，37（1）：37－50.

［12］ Wang J，Feng L，Zhao L，et al.A comparison of two typical multicyclic models used to forecast the world’s conventional oil production［J］.Energy Policy，2011，39（12）：7616－7621.

［13］ Guo X，Li D C，Zhang A.Improved support vector machine oil price forecast model based on genetic algorithm optimization parameters［J］.AASRI Procedia，2012（1）：525－530.

［14］ 李红星.基于统计学习理论的正则化最小二乘回归在时间序列建模和预测中的应用——太阳黑子数、石油价格、汇率的预测［D］.合肥：中国科学技术大学，2007.

［15］ Wang S，Yu L，Lai K.Crude oil price forecasting with TEI＠I methodology［J］.系统科学与复杂性：英文版，2005，18（2）：145－166.

［16］ Xie W，Yu L，Xu S，et al.A new method for crude oil price forecasting based on support vector machines［J］.Lecture Notes in Computer Science，2006，3994：441－451.

［17］ 秦鹏，缪柏其.基于广义指数预报因子的石油价格预测模 型 ［J］.系 统 工 程 理 论 与 实 际，2010，30（8）：1389－1395.

［18］ 赵庆，王志强.基于HP滤波－AR模型－GARCH族模型对黄金价格预测研究［J］.黄金，2014，35（3）：4－8.