基于欧拉方法的机翼表面水滴撞击特性数值模拟

刘 鑫，邢玉明，杜 佶

（北京航空航天大学 航空科学与工程学院，北京100191）

飞机结冰是指飞机在飞行时其外表面上水分积聚冻结成冰的现象。它影响飞机的气动外形、飞行品质及飞行安全，给飞机飞行带来了极大的危害。如：飞机风挡结冰会影响驾驶员视野；测温、测压感头结冰会导致仪表指示失真；机（尾）翼结冰将影响气动外形，增大飞机阻力，减小升力，影响全机操纵性、稳定性；螺旋桨、直升机旋翼结冰会降低升力效率；轴流式压气机进气部件结冰能使发动机熄火等。据统计，大约有9%的飞行事故是由结冰造成的。长期以来，结冰机理和飞机的防／除冰系统一直是国内外飞机系统设计的重要研究课题［1］。

结冰源于云层中的过冷水滴，即低于0℃的液态水滴，过冷水滴是极不稳定的，受到扰动后就可能转化为冰。当过冷水滴撞击到没有采取防冰措施的飞行器表面后，它可能立即结成明冰或向后溢流再结成明冰。研究中，可以通过冰风洞试验、飞行试验和数值计算等途径获取结冰量或结冰区域。但由于试验花费昂贵、周期长且受限于设备条件，很难模拟结冰包线中一些特殊状态。因此美法英等国都在积极研发飞机结冰的数值计算方法和软件。

进行结冰计算的第一步需要计算水滴在模型表面上的撞击特性和收集系数。撞击特性主要通过两种方法来计算：一种是Lagrangian方法；另一种是Eulerian方法。多数结冰计算软件采用Lagrangian方法，在所得流场计算结果的基础上计算过冷水滴的运动轨迹，用来确定水滴在模型表面上的撞击点，从而进一步计算水滴收集系数。Eulerian法由于在计算主流场的同时，也计算得到每一个网格内过冷水滴的质量系数（或体积系数），因此不需要计算过冷水滴在流场中的轨迹。Lagrangian方法对二维或几何形状简单的表面应用起来比较简便，但对多段翼型或发动机进口部件等三维复杂外形，由于粒子释放位置较难确定，很难准确确定撞击极限，且计算时用时较长。而Eulerian方法则不涉及这些问题［2－4］。

本文应用Eulerian方法计算水滴收集系数，采用Fluent商业软件计算空气流场，即将水滴视为拟流体通过Eulerian方法实现水滴流场的求解。

1 数学模型

1.1 基本假设

在Eulerian方法中引入容积分数α的概念。它表示单位体积的混合流体中某一相所占的体积，第q相的容积分数可以表示为αq，q相的体积可以定义为

在结冰条件下，由于水滴的容积分数较小，一般在10－6量级，可认为空气和水滴之间是单向耦合的，即空气流场影响水滴，而水滴对空气流场的影响可以忽略［5－6］。这使得空气相和水滴相可以分离求解：先得到空气流场，再使用空气流场结果计算水滴相。

对Eulerian法中空气和水滴的控制方程可以进行以下假设：

（a）过冷水滴在云层中均匀分布，且以球形存在，不凝聚、不分解、不变形、不破裂；（b）过冷水滴在云层中，不与空气进行热、质交换，即过冷水滴不蒸发、物性参数不变化；（c）忽略作用在水滴上的空气阻力对空气动力的影响；（d）作用在水滴上的作用力仅有阻力和重力；（e）作用在水滴上的阻力是稳态的；（f）空气的紊流脉动不影响水滴的运动。

1.2 控制方程

过冷水滴稳态控制方程如下［5］：

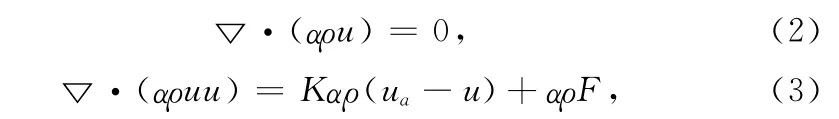
其中，u是水滴的速度矢量，ua是空气的速度矢量，F是作用于水滴上的除阻力之外的力。K为空气－水滴交换系数，由下式给出：

式中，μa为空气的动力黏度，dd是水滴直径，f为阻力函数，对于球形物体的阻力函数可以用下式进行计算：

式中，CD为阻力系数，Re为相对雷诺数，其具体计算公式如下：

式中，ρa为空气密度。

1.3 边界条件

本文借助Fluent软件计算空气流场，其中进口采用速度进口边界条件，出口采用压力出口边界条件，无滑移壁面边界条件，使用k－e湍流模型计算空气流场。将水滴设为拟流体，通过UDS模块求解水滴相控制方程。

水滴相的入口采用速度入口边界条件，速度大小与空气速度相等，出口采用压力出口边界条件。对于水滴相的壁面边界条件需要特殊处理［7］，固体壁面对于空气来说只是普通的固壁，但是对于水滴相来说却相当于一个单向出口，这个出口只容许水滴流出计算域而不容许流入计算域。这是由于水滴在撞击到壁面时会积聚在壁面上而不会从壁面上绕流经过，从而再一次进入计算域中，故而水滴在撞击到壁面时只能流出计算域而不能再次进入。水滴在壁面附近的运动情况如图1所示，当水滴撞击到壁面上时，即水滴速度ud与壁面微元单位法向向量点积小于等于零时，水滴的体积分数与水滴速度保持不变；在非撞击区域，壁面微元单位法向量与水滴速度ud点积大于零时，水滴体积分数取零，水滴速度取下游网格单元速度值。

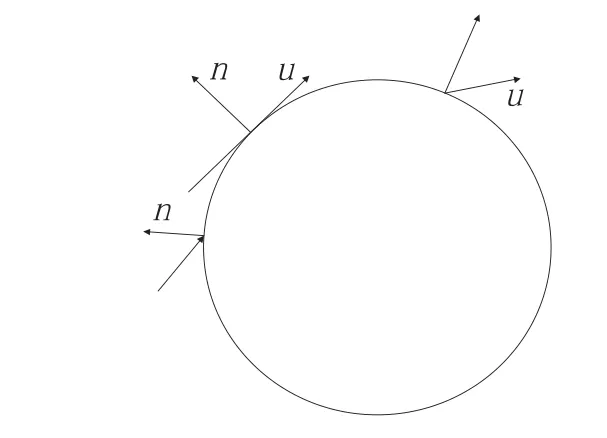
图1 水滴相壁面边界条件

1.4 局部水滴收集系数计算

局部水滴收集系数β为当地表面微元实际水滴收集量与最大可能收集量的比值，其计算公式为：

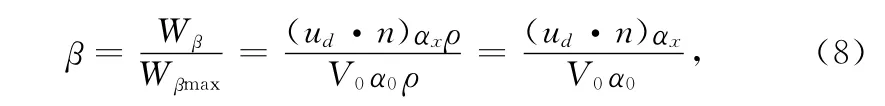
式中，Wβ为实际水滴收集量，Wβmax为最大可能水滴收集量，ud为当地水滴速度矢量，n为部件表面的法向方向矢量，αx为当地水滴体积分数，V0为水滴初始速度，ρ为水滴密度，α0为初始水滴体积分数，可由远场液态水含量计算得出。

2 计算模型及计算条件

2.1 计算模型

本文以NACA0012机翼作为计算模型讨论不同气象条件及飞行速度对水滴撞击特性的影响。计算模型中，翼型弦长1 000mm，在网格划分过程中，在圆柱周围划分10倍远场网格［8］，远场长度方向适当延伸。计算网格如图2－3所示。

图2 流场计算网格

图3 NACA0012计算网格

2.2 计算条件

本文关注不同气象条件及飞行速度对飞行器表面水滴撞击特性的影响，为便于对比分析，并从分析中获得一般规律，选取计算条件如表1所示。

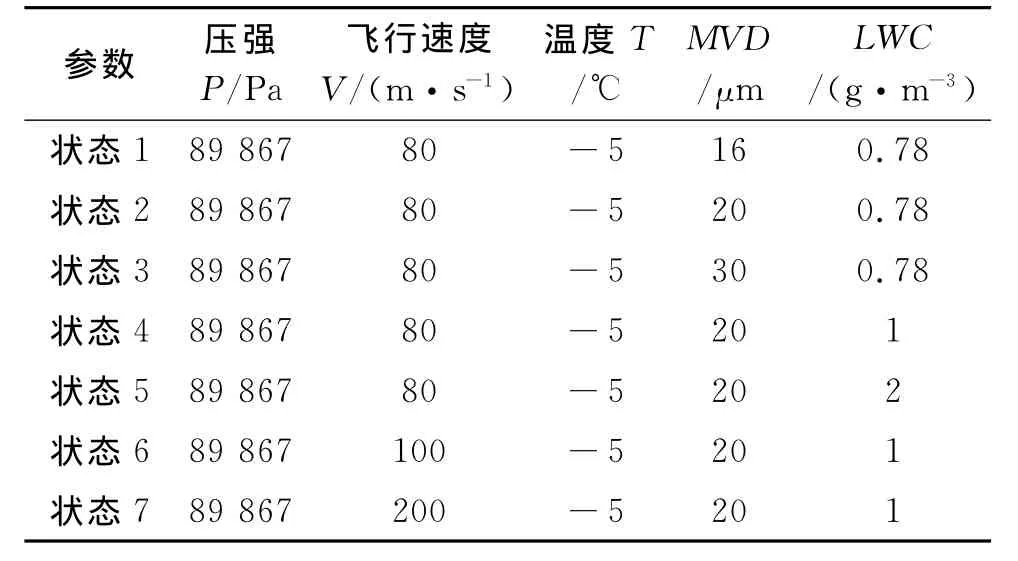
表1 飞行速度及气象条件表

3 计算结果及分析

利用上述计算方法对表1中所列计算条件下NACA0012机翼的水滴撞击特性进行了数值模拟计算。水滴在机翼空气流场中运动，其运动轨迹受到空气黏性阻力的影响。由于水滴具有惯性，因此其保持原有运动形式的趋势撞击到机翼表面。水滴的惯性及受到的阻力与水滴的平均容积直径、来流速度等有关。

选取状态1，取距翼根50mm截面处的计算结果与文献［9］中结果作对比，水滴收集系数分布曲线如图4所示。由图4可知计算结果与文献结果走势符合，因此证明本文计算方法是合理的。

3.1 飞行速度对水滴撞击特性的影响

选取飞行速度不同而其他条件相同的状态4，6，7对水滴撞击特性进行分析，计算结果如图5所示。由计算结果可知，当其他飞行参数和气象条件不变时，飞行速度减小，水滴受到的惯性力减小，惯性对水滴的影响减小，使得阻力对水滴的运动轨迹影响增大。因此，水滴撞击到机翼表面的趋势有所减弱，从而可知机翼水滴局部水收集系数逐渐减小。

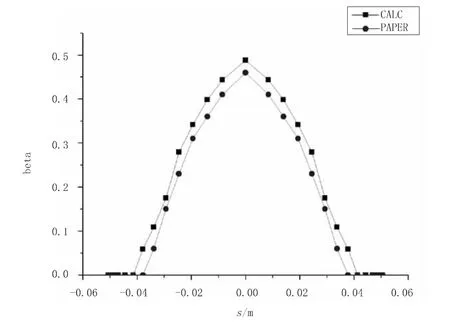
图4 状态1条件下机翼水滴收集系数分布曲线

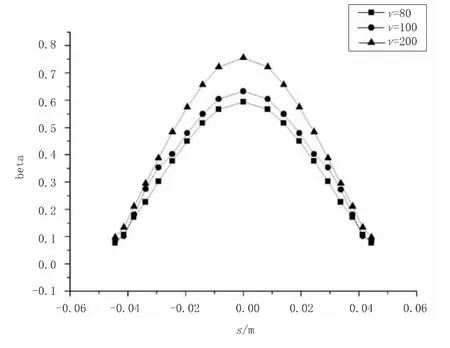
图5 不同飞行速度下机翼水滴收集系数分布曲线

3.2 水滴平均容积直径对水滴撞击特性的影响

选取水滴平均容积直径不同而其他条件相同的状态1，2，3对水滴撞击特性进行分析。随着水滴平均容积直径的增大，水滴本身的惯性也相应增大，惯性力对水滴的影响增加，黏性阻力对水滴轨迹的影响减小，直径大的液滴由于惯性作用，在机翼壁面附近不能像空气流场一样很轻松地绕流，而是直接撞击在壁面上，故而，有图6中所示的计算结果，即水滴收集系数随着水滴平均容积直径的增大而增大，且撞击范围增大。值得注意的是，在水滴平均容积直径超过一定数值时（一般认为是50μm），水滴将会产生沿程参数变化，并在壁面附近产生飞溅、反弹等物理现象，使得撞击特性发生变化［10］。

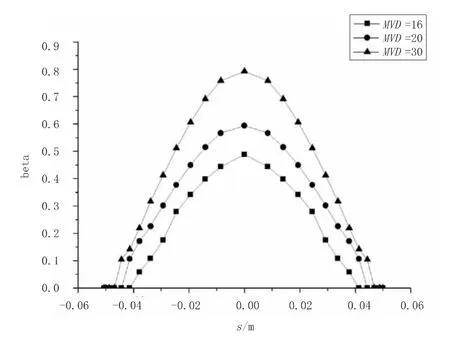
图6 不同平均容积直径下机翼水滴收集系数分布曲线

3.3 不同液态水含量对水滴撞击特性的影响

选取液态水含量不同而其他状态相同的状态3，4，5对水滴撞击特性进行分析，由于在控制方程中，液态水含量的值可以换算出相应的体积分数α值，当水滴流场处于稳态时，即时间导数项为零，方程中体积分数项可以消去，故而液态水含量对水滴撞击特性影响不大，计算结果（见图7）也证明了理论分析的结果，即当液态水含量变化时，机翼附近水滴收集系数基本不变。

图7 不同液态水含量下机翼水滴收集系数分布曲线

4 结论

本文基于欧拉方法计算了不同飞行速度和气象条件下NACA0012机翼水滴撞击特性，使用Fluent商用软件计算空气流场，并通过编制UDS程序求解水滴相控制方程，对水滴相撞击边界条件进行了特殊处理使之更好地反映实际物理过程。从计算结果中可以得出：随着飞行速度的增加，局部水滴收集系数明显上升，水滴撞击范围加大；随着水滴平均容积直径的增加，水滴收集系数上升明显，水滴撞击范围加大；而液态水含量对水滴撞击特性影响不大。

由于水滴平均容积直径对水滴收集系数影响很大，且在水滴直径达到一定数值时（一般为50μm以上），水滴参数沿程会发生改变，并会在壁面上产生飞溅、反弹等现象。故而，在过冷大水滴条件下的撞击特性还有待深入研究。

［1］ 裘燮纲.韩凤华.飞机防冰系统［M］.北京：航空专业教材编审组出版，1985：44－58.

［2］ Mark G Potapczuk.LEWICE／E：An Euler Based Ice Accretion Code［R］.AIAA 92－0037，1992.

［3］ Hedde T，Guffond D.Improvement of the ONERA 3D icing code comparison with 3Dexperimental shapes［R］.AIAA 93－0169，1993.

［4］ Morency F，Heloise Beaugendre，Wagdi G Habashi.FENSAP－ICE：a study of ice shapes on droplet impingment［R］.AIAA 2003－1223，2003.

［5］ Suikno Wirogo，Shashidhar Sriramblatla.An eulerian method to calculate the collection efficiency on two and three dimensional bodies［R］.AIAA 2003－1073，2003.

［6］ Chirag Bhargava，Eric Loth，Mark Potapczuk.Aerodynamic simulations of the NASA glenn icing research tunnel［R］.AIAA 2003－566，2003.

［7］ 杨胜华，林贵平，申晓斌.三维复杂表面水滴撞击特性计算［J］.航空动力学报，2010，25（2）：284－290.

［8］ ANSYS Inc.ANSYS fluent12.0User’s manual［M］.New Hampshire：ANSYS Inc，2009.

［9］ Gray A Ruff，Brian M Berkowitz.User’s manual for the NASA lewis ice accretion prediction code（LEWICE）［R］.NASA，1990：1－27.

［10］ Brahimi M T，Tran P，Chocron D，et al.Effect of supercooled large droplets on ice accretion characteristics［R］.AIAA 97－0306，1997.