一类可映射为Riemann空间的Riemann－Cartan位形空间

王 勇，陈英华

（广东医学院 信息工程学院，广东 东莞523808）

0 引言

非完整约束系统是一类受到不可积分的非完整约束的力学系统。尽管经典力学中的Lagrange原理和Hamilton原理近乎完美地解决了完整约束系统的运动问题，但在将上述理论推广至非完整约束问题时却遇到了极大的困难。“非完整系统和完整系统的差别在于，完整系统的运动可以用第二类Lagrange方程来描述，而非完整系统需用更复杂的微分方程来表征”［1］。从几何的角度看，完整约束系统的位形空间是有曲率、无挠率、且有自然辛结构的Riemann位形空间，而非完整约束系统的位形空间则是有曲率且有挠率的Riemann－Cartan位形空间［2－6］。将完整约束问题的经典分析力学原理推广至非完整约束问题中，本质上是将经典分析力学原理从Riemann位形空间推广至具有更复杂结构的Riemann－Cartan位形空间。一般来说，挠率的存在将破坏系统位形空间的辛结构，这正是无法将基于辛几何的经典分析力学原理直接推广至非完整系统的根本原因。因此，深入研究Riemann－Cartan位形空间的几何结构是研究非完整力学的一项基础且重要的理论工作。

我们在之前的研究中提出，对一阶定常线性约束系统，可以通过约束构造出从高维平直空间到不含约束的、低维位形空间的一阶线性映射，并由此计算出该位形空间的几何结构［4－7］。可以证明，若此约束系统为完整约束系统，则可构造出一阶线性可积映射，与该映射对应的系统的位形空间是无挠率、有曲率的Riemann空间；若此约束系统为非完整约束系统，则构造出的一阶线性映射不可积，与该映射对应的系统的位形空间是有挠率的（一般来说也有曲率）Riemann－Cartan空间，由于此位形空间中存在挠率，因此一般情况下不具有自然的辛结构。

本文将指出，并不是所有的Riemann－Cartan位形空间都没有辛结构。存在一种特殊的Riemann－Cartan位形空间，可以通过引入一个无约束的一阶线性不可积映射，将其映射为一个Riemann位形空间，这说明此类特殊的Riemann－Cartan位形空间本质上就是一个完整约束系统的位形空间，因此也具有辛结构，只不过其辛结构需要通过引入一个合适的无约束的一阶线性不可积映射才能表现出来。

为方便起见，文中采用爱因斯坦求和约定，并对指标取值范围作如下规定：拉丁字母i，j，k，l＝1，2，…，n；罗马字母μ，ν，ρ，σ，λ＝1，2，…，n－m；希腊字母α，β，γ，ξ的取值范围和罗马字母一致。

1 可映射为Riemann空间的Riemann－Cartan位形空间

对由N个粒子组成的、受到3N－m个约束的约束系统，设ciρ为定义在其n维（n＝3 N）平直位形空间［X］（该空间的坐标为xi，度规为gij，联络Γkij＝0）切空间上的一个含约束的线性映射，即

考虑式（3）可知，空间［W］的挠率不为零，空间［W］是一个Riemann－Cartan位形空间。

考虑到矩阵（珘bαρ）非奇异，我们可以在 Riemann－Cartan位形空间［W］中引入如下无约束的一阶线性不可积映射：

映射（6）将Riemann－Cartan位形空间［W］映射为一个新的空间［Q］，且空间［Q］的度规和联络分别为：

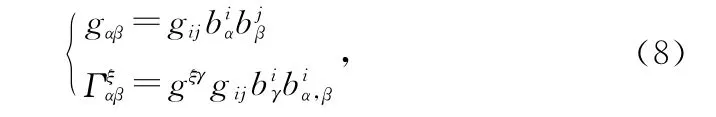
考虑式（3）可知，空间［Q］的联络关于下脚标对称，该空间的挠率为零，即：

说明空间［Q］是一个完整约束系统的、具有自然辛结构的Riemann位形空间。

显然，由映射（1）所定义的m维Riemann－Cartan位形空间［W］是一个特殊的Riemann－Cartan空间。虽然由于挠率的存在，位形空间［W］不具有自然的辛结构，但通过引入一个合适的无约束的一阶线性不可积映射珘aρα，就可以将其映射为一个完整约束系统的、具有自然辛结构的Riemann位形空间［Q］。这说明虽然位形空间［W］具有挠率，但其本质上是一个完整约束系统的位形空间，因此也具有辛结构，只不过其辛结构需要通过引入一个合适的无约束的一阶线性不可积映射才能表现出来。

2 算例

设［X］是一个受到约束的、具有单位质量的质点的三维平直位形空间，通过如下非完整线性映射

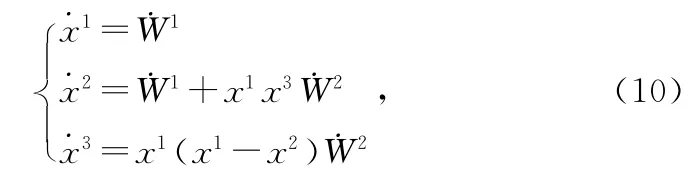
用一阶线性映射的方法可计算其位形空间［W］的联络为：

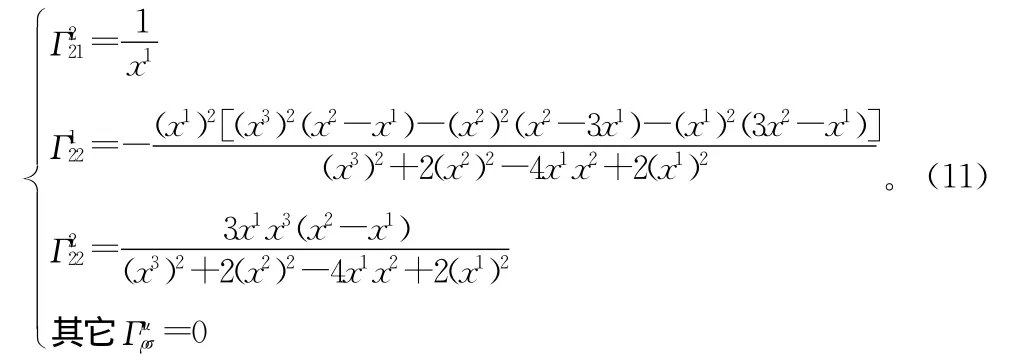
空间［W］的联络关于下脚标不对称，其挠率为：

说明位形空间［W］是一个Riemann－Cartan空间。

若引入一个不可积映射

则通过计算可得位形空间［Q］的联络为：

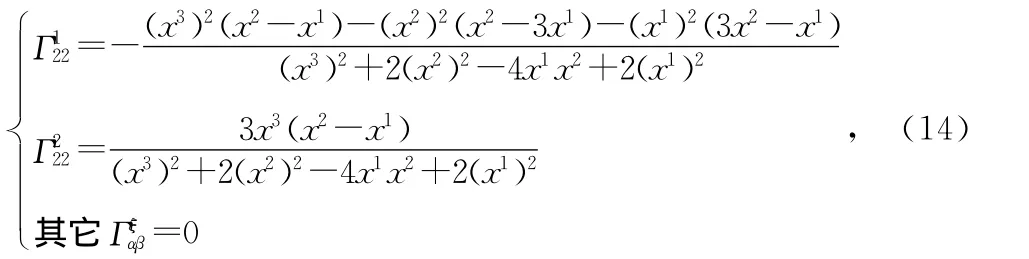
显然空间［Q］的联络关于下脚标对称，其挠率全部为零，说明空间［Q］是一个无挠率的Riemann位形空间。

上述结果说明，由式（10）所定义的空间［W］是一个可映射为Riemann空间的特殊的Riemann－Cartan位形空间，因而本质上是一个完整约束系统的、具有辛结构的Riemann－Cartan位形空间。事实上，从式（10）可直接通过积分得到系统所受完整约束为：

3 结论

尽管就一般而言，Riemann－Cartan位形空间中的挠率将破坏其辛结构，但确实存在一种特殊的、本质上具有辛结构的Riemann－Cartan位形空间。通过引入一个恰当的无约束的一阶线性不可积映射，可以将此类特殊的Riemann－Cartan位形空间映射为一个Riemann位形空间，这说明此类特殊的Riemann－Cartan位形空间本质上就是一个完整约束系统的位形空间。从力学的角度看，上述引入的无约束的一阶线性不可积映射相当于是此类特殊的Riemann－Cartan位形空间与一个完整约束系统的Riemann位形空间之间的“准坐标变换”。

［1］ 梅凤翔.分析力学［M］.北京：北京理工大学出版社，2013：309.

［2］ Kleinert H，Shabanov S V.Space with torsion from embedding，and the special role of autoparallel trajectories［J］.Phys Lett B，1998，428：315－321.

［3］ Kleinert H，Pelster A.Autoparallels from a new action principle［J］.Gen Rel Grav，1999，31（9）：1439－1447.

［4］ Guo Y X，Wang Y，Chee G Y，et al.Nonholonomic versus vakonomic dynamics on a Riemann－Cartan manifold［J］.J Math Phys，2005，46（5）：062902.

［5］ 王勇，郭永新.Riemann－Cartan空间中的d’A1embert－Lagrange原理［J］.物理学报，2005，54（12）：5517－5520.

［6］ 王勇，郭永新，吕群松，等.非完整映射理论与刚体定点转动 的 几 何 描 述 ［J］.物 理 学 报，2009，58（8）：5142－5149.

［7］ Guo Yongxin，Liu Chang，Wang Yong，et al.Nonholonomic mapping theory of autoparallel motions in riemann－cartan space［J］.Science China（physics，mechanics ＆ Astronomy），2010（9）：1707－1715.