(n，n)扶椅型单臂ZnO纳米管的第一性原理

刘竹琴，张富春，张威虎

(延安大学物理与电子信息学院，陕西延安 716000)

自从日本科学家Iijima发现了单臂碳纳米管以来［1］，实验和理论研究都证实了碳纳米管具有新颖奇特的电学、光学和磁学属性，在纳米材料和凝聚态物理等领域展现出了广阔的应用前景［2-4］。碳纳米管以及石墨烯材料的研究成果推动了各国科学家对其他纳米管材料的研究热潮。目前科学家逐渐开展了对手性特征并不十分敏感的其他纳米管的研究工作，包括 ZnO纳米管［5-7］、BN 纳米管［8］和 SiC 纳米管［9］等。特别是ZnO是一种新型的Ⅱ-Ⅵ族直接宽禁带氧化物半导体材料，在室温下ZnO的禁带宽度是3.27 eV，激子束缚能高达60 meV，与Si，GaAs和GaN等光电子材料相比，ZnO具有低的介电常数、大的光电耦合率和优异的化学稳定性，同时，ZnO材料也具有优异的压电和光电特性，是一种在紫外和蓝光发射方面具有潜在应用前景的新型光电子材料，目前已在太阳能电池［10］、气敏传感器［11］、显示器件［12］、透明导电薄膜［13］和紫外半导体器件［13］等方面显示出了广泛的应用前景。这主要是由于ZnO纳米管材料除了具有半导体材料的优异性能外，一维ZnO纳米管材料还具有比表面积大以及优异的表面效应和量子尺寸效应等优异特性。在ZnO纳米管的研究方面，Zhou等人［15］利用微波加热制备方法合成了直径和长度达到10 μm和100 μm 的六角形ZnO 纳米管。Zhang等人［16］用Zn纳米线为模板，采用微波等离子体制备方法合成了ZnO纳米管。Xing等人在氧化气氛中［17］采用简单的热蒸发法合成了ZnO纳米管。Xu等人［18］成功合成了壁厚15nm、管径在50～100nm范围的ZnO纳米管。Xing等人［19］也利用化学合成法合成了壁厚达4 nm、管径达30～100 nm的多臂ZnO纳米管材料。Tu等人［20］采用固相合成技术成功合成了ZnO纳米管材料，研究显示具有优异的发光特性，以上的研究成果促进了一维ZnO纳米管材料在光电子领域的研究进展。但就目前的研究现状而言，对ZnO纳米管的认识仍然处于开始阶段，ZnO纳米管目前在实验还没能成功制备出。因此，ZnO纳米管的结构和属性的理论和实验研究就显得尤为必要。我们将采用第一性原理计算方法研究单臂扶椅型ZnO纳米管的几何结构以及电学和光学性质，研究结果将为设计和制备一维ZnO纳米管材料提供必要的理论和实验指导。

1 模型建立与计算方法

1.1 模型建立

(n，n)扶椅型单臂ZnO纳米管的理论模型采用碳纳米管模型构建方法。图1(a)显示的是ZnO的单层结构模型，其中，T和 Ch分别代表ZnO纳米管的平移矢量和手性矢量，d代表最近邻原子之间的键长，因此可以得出以下表达式

当m=n时，纳米管表示为扶椅型纳米管，其中Ch=(n，n)，具体卷曲构造的模型如图1和图2所示，具体构造时，我们以直线OB为旋转轴，如图所示沿OA卷曲二维平面OAB'B，当A点和O点重合，B'点和B点重合，此时形成的模型为(n，m)ZnO纳米管。

图1 ZnO单层模型 (黑色为O原子，灰色为Zn原子)Fig.1 The models of single layer for ZnO(the black and grey balls represent oxygen and zinc atoms)

图2 (4，4)扶手椅型单臂ZnO纳米管(黑色球为O原子，灰色球为Zn原子)Fig.2 The single-walled(4，4)ZnO NT(the black and grey balls represent oxygen and zinc atoms)

1.2 计算方法

计算采用密度泛函理论下的第一性原理计算方法［21］，在计算过程中，首先我们对(n，n)扶椅型单臂ZnO纳米管进行几何结构优化计算，获得稳定的(n，n)扶椅型单臂ZnO纳米管结构。其次，对优化后的(n，n)扶椅型单臂ZnO纳米管进行能量和基本属性的计算，具体参数设置如下:选用广义梯度近似方法处理电子与电子之间的交换关联能，关联函数采用PW91函数，采用超软赝势平面波来描述离子实和价电子之间的相互作用势，计算中氧原子和锌原子的价电子组态我们分别选取为:O-2s23p4，Zn-3s22d10，平面波截断能量选取360 eV，迭代收敛精度选取为 1×10-5eV，内应力不大于0.1 GPa，每个原子上的作用力小于0.5eV/nm，布里渊区K点选取为1×1×16。

2 结果与讨论

2.1 几何结构与稳定性分析

首先，分析(n，n)扶椅型单臂ZnO纳米管的结构和稳定性，几何结构优化结果显示弛豫后的扶椅型单臂ZnO纳米管都变成规则的圆柱形管状结构，与碳纳米管结构相同，单臂ZnO纳米管体系中的O原子和Zn原子沿纳米管的管璧向外和向内都发生了驰豫现象。同时，每个O原子和Zn原子都与3个最近邻的原子成键，结果与已有的实验和理论结果吻合［16，20，22-23］。表 1 是优化后的扶椅型ZnO纳米管的几何结构参数与结合能数据。从表1可以看出，随着ZnO纳米管直径的减小，扶椅型ZnO纳米管的禁带宽度Eg逐渐增大，单臂ZnO纳米管出现了明显的量子尺寸效应。但是，体系的结合能却随着纳米管管径的减小而逐渐增大，纳米管体系的稳定性开始下降，这些结果表明扶椅型单臂ZnO纳米管的管径越大，纳米管的构型就越稳定。另外，随着纳米管管径的逐渐增大，沿［0001］方向的Zn-O键长逐渐缩短，理论计算的 Zn-O键长在0.1.886 nm～0.192 3 nm范围之间。

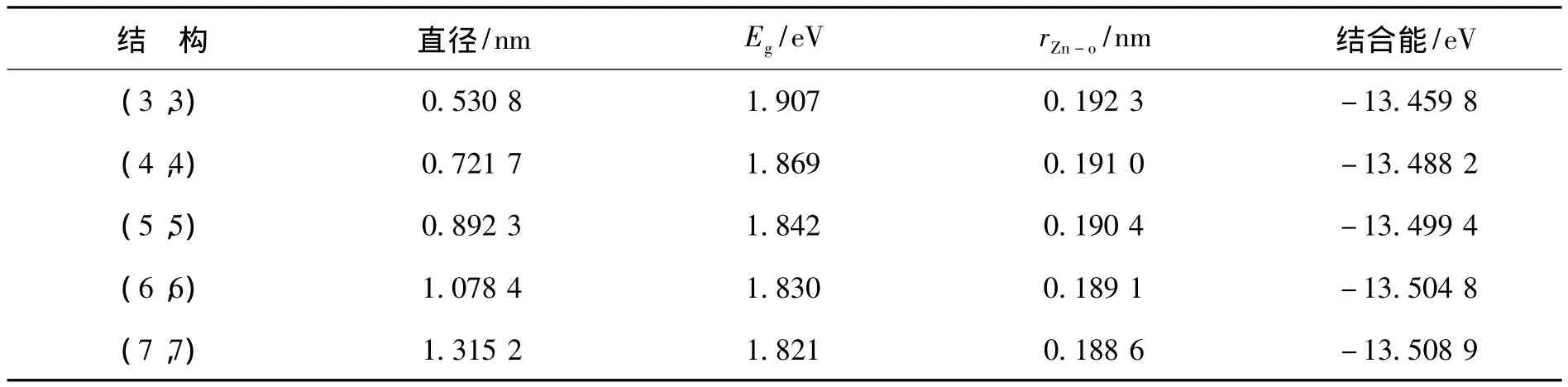
表1 (n，n)扶椅型ZnO纳米管几何参数、带隙、键长和结合能Tab．1 Calculated Bind Energy，band gap Eg，bond lengths and Diameters

2.2 电子结构分析与讨论

图3是计算的(n，n)扶椅型单臂ZnO纳米管的能带结构。从图中可以看出，(n，n)扶椅型单臂ZnO纳米管理论预测是一直接宽禁带半导体材料，价带顶和导带底都位于布里渊区中心Γ点，我们计算的禁带宽度范围在1.821 eV-1.907eV之间，计算的带隙值明显大于理论预测的ZnO体材料的值0.92 eV，这里出现的单臂ZnO纳米管带隙展宽效应主要是由于纳米管的径向限制效应现象造成的［24-25］。但明显小于ZnO体材料的实验值3.37 eV。这是由于广义梯度近似和局域密度近似都存在计算的带隙值偏低的问题，因为在第一性原理计算中采用的主要是密度泛函理论中的基态性质，但带隙主要是由激发态的性质决定的，因此计算的ZnO的带隙值偏低。另外，图3中扶椅型单臂ZnO纳米管能带结构计算结果揭示沿 Γ(0，0，0)2π/c→Z(0，0，0.5)2π/c方向，ZnO纳米管最低未据态出现了明显的弥散性特征，而最高占据态的弥散性却开始减弱，局域性逐渐增强。

图3 ZnO纳米管的能带结构Fig.3 Band structures of ZnO NTs

为了更进一步研究(n，n)扶椅型单臂ZnO纳米管的属性，我们也计算了(n，n)扶椅型单臂ZnO纳米管的总体态密度和分波态密度，具体计算结果如图4、图5和图6所示。从图中可以看出，当ZnO纳米管的直径减小，纳米管的价带宽度都被略微展宽，整体纳米管的价带都向低能方向发生了漂移，表面缺陷态能级出现在了纳米管的价带顶。从图5和图6可以看出，扶椅型单臂ZnO纳米管的上价带 (-4.3 eV～0 eV)主要是由O原子的2p态电子形成的;而下价带(-6.9 eV～-4.3eV)主要由Zn原子的3d态电子和部分O原子的2p态电子形成的，特别是在纳米管的价带顶附近出现了O 2p态贡献态密度峰，此态密度峰是O原子的2p态电子贡献的表面缺陷态能级。从图5和图6中可以看出，Zn原子的3d轨道和O原子的2p轨道之间在下价带区出现了强烈的轨道杂化现象，从而展宽了价带，造成禁带宽度变小。对于导带部分，从图5和图6可以看出，扶椅型单臂ZnO纳米管的导带由Zn 3p态和Zn 4s态贡献，导带的态密度峰出现了弥散性特征。同时，最高占据态是由O 2p态贡献，最低未占据态由Zn 4s态贡献，即扶椅型ZnO纳米管的禁带宽度由O 2p态和Zn 4s态共同决定的［25］。

2.3 扶椅型ZnO纳米管光学属性研究

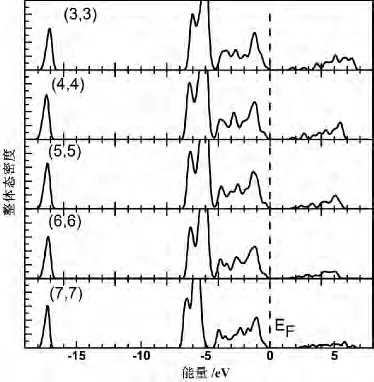
图4 ZnO纳米管总体态密度Fig.4 The TDOS of ZnO NTs

图5 ZnO纳米管O原子的分波态密度Fig.5 The PDOS of O atoms for ZnO NTs

图6 ZnO纳米管Zn的分波态密度Fig.6 The PDOS of Zn atoms for ZnO NTs

图7(a)是此次计算得到的扶椅型单臂ZnO纳米管介电函数虚部。在图7(a)中的低能区(0～4eV)存在一个强烈的介电峰，该介电峰位于2.75～2.60 eV附近，随着纳米管管径的增大，介电峰强度明显增大，并且向低能方向发生了微小的漂移，出现了明显的蓝移现象，这主要是由于扶椅型单臂ZnO纳米管的禁带宽度随着纳米管管径的增大出现了明显的量子效应造成的。另外，从扶椅型单臂ZnO纳米管的能带结构和态密度图可知，该介电峰来源于纳米管价带顶O原子的2p轨道电子到导带底Zn原子的4s轨道电子的跃迁。在能量区 (4.0～7.0 eV)，介电函数虚部也出现了一些明显介电峰，从分波态密度图可知，这些介电峰来源于Zn原子的3d轨道电子到O原子的2p轨道电子的跃迁。

图7(b)是扶椅型ZnO纳米管的吸收光谱图，从图中可以看出，扶椅型ZnO纳米管的本征吸收开始发生(对应于纳米管的禁带宽度1.8 eV)，当光子能量大于2.0 eV，ZnO纳米管的光吸收系数急剧增加，光吸收增强，表明由价带顶电子到导带底电子的直接跃迁几率增大。当光子能量达到3.0 eV时，光吸收系数开始逐渐减小，图中出现了吸收肩。同时，在4.2 eV附近有一个微弱的吸收峰，该吸收峰主要由O 2P态电子到导带底的跃迁形成的［25］。计算结果揭示了ZnO纳米管的吸收边带边都随着纳米管管径的增大而向低能方向发生了微小的漂移现象，以上分析结果与复介电函数谱的分析结果是吻合的。总之，从吸收谱和复介电谱的计算结果分析可知，扶椅型单臂ZnO纳米管是一种优异蓝光和紫外光发射材料。

图7 扶椅型ZnO纳米管的光学属性Fig.7 The optical properties of armchair ZnO NTs

3 结论

本文采用基于密度泛函理论框架下的第一性原理计算方法，研究了扶椅型单臂ZnO纳米管的电子结构和基本属性。研究结果显示扶椅型单臂ZnO纳米管都具有与C纳米管一样的圆柱形管状结构，能量计算结果表明纳米管是可以稳定形成的;扶椅型单臂ZnO纳米管是一直接宽带隙半导体纳米材料，随着扶椅型单臂ZnO纳米管管径的逐渐增大，纳米管的整体价带被明显展宽，价带都向低能方向发生了明显的移动，在纳米管的价带顶附近出现了表面缺陷态能级。光学性质计算结果显示扶椅型单臂ZnO纳米管在0～7.0 eV的能量区出现了明显的介电峰，吸收带边对应于紫外波段，与ZnO体材料相比，发生了明显的蓝移现象，具有优异的紫外光和蓝光发射能力。

［1］ IIJIMA S.Helical microtubules of graphitic carbon［J］.Nature，2001，354:56-58.

［2］ BALL P.Roll up for the revolution ［J］.Nature，2001，414:142-146.

［3］ BAUGHMAN R H，ZAKHIDOV A A，WALT A.Carbon nanotubes，the route toward applications［J］.Science，2002，297:787-792.

［4］ BAUGHMAN R H.Muscles made from metal［J］.Science，2003，300:268-269.

［5］ CHENG J P，GUO R Y，WANG Q M.Zinc oxide single-crystal microtubes ［J］.Appl Phys Lett，2004，85:5140.

［6］ YU H D，ZHANG Z P，HAN M Y，et al.A general low-temperature route for large-scale fabrication of highly oriented zno nanorod/nanotube arrays［J］.J Am Chem Soc，2005，127:2378-2379.

［7］ WEI A，SUN X W，XU C X，et al.Stable field emis-sion from hydrothermally grown ZnO nanotubes［J］.Appl Phys Lett，2006，88:213102.

［8］ WIRTZ L，MARINI A，RUBIO A.Excitons in boron nitride nanotubes:dimensionality effects［J］.Phys Rev Lett，2006，96:126104.

［9］ PEI L Z，TANG Y H，CHEN Y W，et al.Preparation of silicon carbide nanotubes by hydrothermal method［J］.J Appl Phys，2006，99:114306.

［10］ ZAERA R T，ELIAS J，CLÉMENT C L.ZnO nanowire arrays:Optical scattering and sensitization to solar light［J］.Appl Phys Lett，2008，93:233119.

［11］ AHN M W，PARK K S，HEO J H，et al，Gas sensing properties of defect-controlled ZnO-nanowire gas sensor［J］.Appl Phys Lett，2008，93:263103.

［12］ LI C，LEI W，ZHANG X B，et al.Fabrication and field emission properties of regular hexagonal flowerlike ZnO nanowhiskers［J］.J Vac Sci Technol B，2007，25(2):590-593.

［13］MINAMI T，OHTANI Y，MIYATA T，et al.Transparent conducting Al-doped ZnO thin films prepared by magnetron sputtering with dc and rf powers applied in combination ［J］.J Vac Sci Technol，2007，25(4):1172-1177.

［14］ LEONG E S P，YU S F，LAU S P.Directional edgeemitting UV random laser diodes［J］.Appl Phys Lett，2006，89:221109.

［15］ ZHOU J，WANG Z D，WANG L，et al.Synthesis of ZnO hexagonal tubes by a microwave heating methods［J］.Superlattices and Microstructures，2006，39:314-318.

［16］ZHANG X H，XIE S Y，JIANG Z Y，et al.Rational design and fabrication of ZnO nanotubes from nanowire templates in a microwave plasma system ［J］.J Phys Chem B，2003，107(37):10114-10118.

［17］XING Y，XI Z H，XUE Z Q，et al.Optical properties of the ZnO nanotubes synthesized via vapor phase growth ［J］.Appl Phys Lett，2003，83:1689-1691.

［18］XU W Z，YE Z Z，MA D W，et al.Quasi-aligned ZnO nanotubes grown on Si substrates［J］.Appl Phys Lett，2005，87:093110.

［19］ XING Y J，XI Z H，ZHANG X D，et al.Nanotubular structures of zinc oxide［J］.Solid State Communications，2004，129:671.

［20］ TU Z C，HU X.Elasticity and piezoelectricity of zinc oxide crystals，single layers，and possible singlewalled nanotubes［J］.Phys Rev B，2006，74:035434.

［21］ KRESSE G，FURTHMÜLLER.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set［J］，Phys Rev B，1996，54:011169.

［22］KONG X，SUN X，LI X，et al.Catalytic growth of ZnO nanotubes［J］.Mater Chem Phys，2003，82:997.

［23］XU C X，ZHU G P，LI X，et al.Growth and spectral analysis of ZnO nanotubes［J］.J Appl Phys，2008，103:094303.

［24］ XIANG H J，YANG J L，HOU J G，et al.Fabrication of nanoscale gaps using a combination of self-assembled molecular and electron beam lithographic techniques［J］.Appl Phys Lett，2006，88:223111.

［25］张富春.3d过渡金属掺杂一维ZnO纳米材料磁光机理研究［D］.西安:中国科学院研究生院(西安光学精密机械研究所)，2009.