求解0－1背包问题的动态规划改进算法分析

李军民，傅云凤

(西安科技大学计算机学院，陕西西安 710054)

0-1背包问题［1］是一个典型的NP难问题，可作为许多工业场合的应用模型，如资本预算、货物装载和存储分配问题等。对该问题的求解，既具有理论价值又具有实际意义。目前已有的求解方法可分为两大类，一类是精确算法，如动态规划算法［2］、回溯法［3］、分支限界法［4］;另一类是近似算法，如贪婪法［5］、蚁群算法［6］和遗传算法［7］。本文对文献［8］中的动态规划改进算法进行分析，此算法存在不足之处:其空间资源浪费较大。为了克服这一缺点，本文提出了采用动态链表存储数据的实现方式改进此算法，从而达到改善其空间复杂度的目的。

1 问题描述

给定n种物品和一个背包，对n种物品进行编号 1，2，…，n，物品 i的重量 wi，其价值 pi，背包容量为 c，给定c ＞ 0，wi＞ 0，pi＞ 0，1≤i≤n，要求找出一个 n 元向量(x1，x2，…，xn)，xi∈ {0，1}，使得达到最大。

2 求解0－1背包问题的动态规划算法

2.1 0－1背包问题的最优子结构性质

根据0－1背包问题的描述，其具有最优子结构和重叠子问题性质。最优子结构即:设(x1，x2，…，xn)是0－1背包问题的最优解，则(x2，x3，…，xn)是子问题(从物品2至物品n中选取，装入背包)的最优解。

2.2 规划数学模型

设m(i，j)是背包容量为j时，可选物品是i，i+1，…，n时0－1背包问题的最优值。则可建立递归关系式

3 一种动态规划法的改进算法分析

3.1 该动态规划改进算法的思路

由m(i，j)的递归式可知，在一般情况下，对每一个确定的i，函数m(i，j)是关于变量j的阶梯状单调不减函数［8］。跳跃点［9］是这一类函数的描述特征。在一般情况下，函数m(i，j)由全部跳跃点唯一确定，因此，针对每一个i值，只记录m(i，j)的跳跃点(j，m(i，j))也可求出背包问题的最优解和最优值。

该算法对于每一个确定的i采用表c［i］来记录函数m(i，j)的全部跳跃点。c［i］可依据式(1)和式(2)递归的由c［i+1］得到，初始时令c［n+1］={(0，0)}。函数m(i，j)的全部跳跃点是函数m(i+1，j)的跳跃点集c［i+1］和函数m(i+1，j－ wi)+pi的跳跃点集d［i+1］的并集，d［i+1］由c［i+1］来确定，公式如下

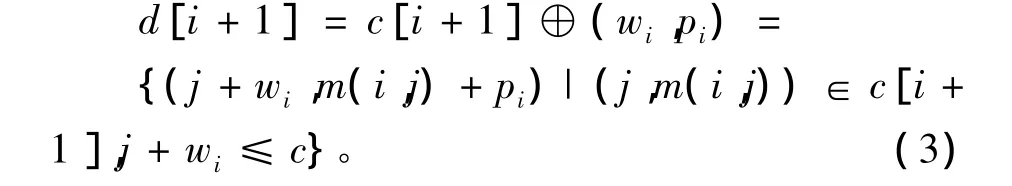
设(a，b)和(c，d)是 c［i+1］∪ d［i+1］中的两个跳跃点，当c≥a且d＜b时，(c，d)受控于(a，b)，将(c，d)删除。因此，在由 c［i+1］计算c［i］的过程中，先由 c［i+1］计算 d［i+1］，再合并 c［i+1］和 d［i+1］，并清除受控点得到 c［i］。

3.2 该动态规划改进算法的分析

此算法采用二维数组c［］［2］记录跳跃点的坐标值(j，m(i，j))，从而实现表 c［i］对跳跃点的记录。此算法的空间复杂度在于跳跃点集(j，m(i，j))(1≤i≤n，0≤j≤c)存储所占用的空间，因此其空间复杂度为

此算法对于每一次求得的跳跃点集c［i］(1≤i≤n)都记录于二维数组c［］［2］中，跳跃点集c［i+1］和c［i］存在相同的跳跃点，这些相同的跳跃点需要重复记录于数组中，且使用静态数组，事先需要定义较大的数组来避免溢出的发生，这样使得空间资源浪费较大。

4 利用动态链表记录跳跃点改进上述算法

为了克服上述算法求解0－1背包问题的不足，本文采用动态链表结构存储跳跃点集，来减轻空间资源的浪费，其算法介绍如下。

4.1 改进算法的思路

1)对每一个确定的i，仍用一个表c［i］来存储函数m(i，j)的全部跳跃点(j，m(i，j))(0 ≤j≤c)，但采用动态链表结构实现表c［i］对跳跃点集的记录。

2)由式(1)和式(3)可知，跳跃点集c［i］可由表 c［i+1］和表 d［i+1］确定，表 d［i+1］可由c［i+1］确定。初始时，令c［n+1］={(0，0)}，新建一个链表结点，其重量和价值均为0，以此来实现对跳跃点(0，0)的记录。

3)由式(3)求跳跃点集d［i+1］时，设置一个布尔型变量，标识表d［i+1］中每次求得的点是否受控。将上述判断受控点的标准改为:设∃∀(a，b)∈c［i+1］，∃∀(c，d)∈d［i+1］，当a ＞ c，b≤ d 或 a=c，b ＜ d 时，(a，b)受控于(c，d);当 c≥ a，d ≤ b时，(c，d)受控于(a，b)。每次求得表d［i+1］中的一个点时，判断其是否为受控点，若不为受控点，将其加入链表;否则，舍弃;同时查看表c［i+1］中的点是否受控，若受控，则标记其为新增受控点。

4)在求得跳跃点集d［i+1］后，遍历整个链表，若链表中的结点被标记为新增受控点，则标记该结点已受控。遍历链表结束时，没有标记为已受控的跳跃点集就是 c［i］。这样就由表 c［i+1］和表 d［i+1］求得表 c［i］。

5)按照上述方法，可递归地求出表c［1］，它记录了m(1，j)的全部跳跃点。由于链表中记录的跳跃点不是按照m(i，j)值由小到大的顺序排列的，需要遍历链表寻求价值最大的结点，该结点的价值即为最优值。

6)构造最优解，其步骤为:

Step1 初始时，令i=1，y初始化为式(5)中求得的价值最大的结点的重量值j0，m初始化为该结点的价值m(1，j0)。

Step 2 遍历链表中的所有结点(j，m(i，j))(1 ≤ i≤ n，0 ≤ j≤ c)，如果 ∃(j'，m(i'，j'))使 j'+wi=y，m(i'，j')+pi=m 成立，则 xi=1，y=j'，m=m(i'，j');否则 xi=0;然后令 i++。

Step 3 重复Step2，直至i＞n为止。

4.2 改进算法的分析

此改进算法采用动态链表记录跳跃点集，其空间复杂度在于跳跃点集的存储。但是，不需要重复记录已存在的跳跃点，只需将每次求得的新增跳跃点加入，又每次求得的跳跃点个数不超过2i，故最终求得的跳跃点总数不超过2n。因此，空间复杂度为O(2n)。

该方法递归地求出跳跃点集c［1］，不需要重复记录已存在的跳跃点。所以不存在同一跳跃点的重复记录问题，且采用动态链表结构记录跳跃点，大大节省了空间资源，弥补了采用二维数组记录跳跃点这种动态规划改进算法的不足。

5 算法测试实例

有5种物品和一个背包，背包容量为100，装入的物品不可分割，求取此0－1背包问题的最优解和最优值。每种物品的重量和价值如表1所示。

动态规划法、二维数组记录跳跃点的动态规划改进算法和动态链表记录跳跃点的动态规划改进算法，采用i记录物品编号，利用数组w［n］记录物品重量，数组p［n］记录物品价值，bestp记录最优值，x［n］记录最优解。3种方法解决本例中的0－1背包问题的运行结果对比如表2所示。程序运行时间以秒为单位，n值较小时，3种方法的程序运行时间几乎没有差异;当n值取100时，动态链表记录跳跃点的动态规划改进法的运行时间较前两种方法在十分位出现差异。

表1 背包问题信息表Tab．1 Information sheet of knapsack problem

表2 3种方法解决0－1背包问题的运行结果比较Tab．2 Comparison of computational results of three methods solving 0 －1 knapsack problem

表2表明，采用上述3种方法，该0－1背包问题的最优解、最优值和装入背包的重量均相同，进而表明动态链表结构记录跳跃点集的动态规划改进算法的有效性。通过空间复杂度的对比，验证了动态链表结构记录跳跃点集的实现方式在降低空间复杂度方面的优越性。

动态规划法的空间复杂度在于记录函数m(i，j)的值，空间复杂度为 Ω(nc)。二维数组存储跳跃点的动态规划改进法的空间复杂度为，动态链表记录跳跃点的动态规划改进法的空间复杂度为O(2n)。前两种方法均采用二维数组存储数据，为了避免溢出情况的发生，需要预先定义较大的存储空间。随着n值的增大，且在c值较大的情况下，动态链表结构记录跳跃点集的实现方式在降低空间复杂度方面的优越性越明显。

6 结语

本文基于动态规划法的一种改进策略，进行算法分析，进而提出其改进算法，改善了原算法的空间复杂度。通过实例验证了该改进算法的有效性，且证实其空间复杂度的优越性。随着n值的增大，且在c较大的情况下，此改进算法的空间复杂度优越性越明显;但是，它的程序运行时间较前两种方法要长一些。为了使该改进算法的应用价值更好地发挥出来，今后，将尝试利用该改进算法的思想解决其他问题。

［1］ 王晓东.计算机算法设计与分析［M］.北京:电子工业出版社，2012，2.

［2］ 唐敏，刘冠蓉.用动态规划法和贪心法解决背包问题［J］.软件导刊，2007(5):111-113.

［3］ 刘继，夏定纯.用动态规划法与回溯法实现0-1背包问题的比较［J］.科技信息，2010(19):458.

［4］ 赵鑫.0/1背包问题分支限界法在C++程序实现中的难点解析［J］.产业与科技论坛，2012(3):69-70.

［5］ 蒋力，武坤.0-1背包问题贪婪算法应用研究［J］.计算机与数学工程，2007(6):32-33.

［6］ 秦玲，白云.解0-1背包问题的蚁群算法［J］.计算机工程，2006(6):212-214.

［7］ 王莉，绍定宏.基于遗传算法的0/1背包问题求解［J］.计算机仿真，2006(3):154-156.

［8］ 吕聪颖，赵刚彬.求解0-1背包问题的动态规划分析［J］.南阳理工学院学报，2011(2):17-21.

［9］ LEVITIN A.算法设计与分析基础［M］.北京:清华大学出版社，2004.