动力电池荷电状态估算方法的研究
方小斌
(珠海格力电器股份有限公司,广东 珠海519070)
0 引 言
随着绿色、环保、节能的呼声日益高涨,新一代电动车作为无污染、能源多样化配置的新型交通工具,引起了人们的普遍关注并得到了极大的发展。
电动汽车(EV,Electric vehicle)主要有三种类型:电池电动车(BEV,Battery Electric vehicle),混合电动车(HEV,Hybrid Electric vehicle),燃料电池电动车(FCEV,Fuel Cell Electric vehicle)。动力电池作为电动汽车的能源之一,为确保电池组性能良好并延长使用寿命,必须对其进行必要的管理和控制。实现这一目标的前提是准确可靠地获得电池现存的容量状态参数。用可测得电池参数对现存电池容量状态做出准确、可靠的估计,一直是电动汽车和电池研究人员十分关注并投入大量精力的研究课题。目前,国内外普遍地采用电池荷电状态(SOC,State of Charge)来描述电池容量状态。
电池本身的特性决定了电池电量的预测成为电动汽车开发的一个难点。目前大多数电动汽车采用的电量预测技术包括了开路电压法、负载电压法、内阻法、电量累积法、BP神经元网络法以及上述方法的组合等。但这些方法都难以精确地测量蓄电池的剩余电量,并以此为依据计算电动汽车蓄电池的荷电状态(SOC)。
本文在安时法的基础上,用开路电压法对电池的初始容量进行估计,把其它对动力电池的影响因素作为系统噪声,采用卡尔曼滤波最小方差估计最优化递推,在有测量噪声环境中对动力电池的荷电状态进行实时滤波与估计,使安时法在大范围内有较高的精度。
1 电池荷电状态SOC估算方法
1.1 常规电池荷电状态SOC估算方法
目前电池荷电状态SOC的估算方法主要有:
(1)电量累积法(安时法)
安时法的原理较为简单。它将电池视为一个封闭的对象系统,并不去研究相对而言较为复杂的电化学反应及电池内部各个参数之间的关系。而是着眼于该系统的外在特征,如在电量监测中进出电池这一封闭系统的电量。通过累积电池在充电或放电时的电量来估计电池的SOC,并根据电池的温度、放电率对SOC进行补偿。
(2)电阻测量法(内阻法)
电池的内阻包括欧姆内阻和极化电阻两部分,二者之和为电池的全内阻。其内阻同电池电解液比重一样,与电池剩余电量有着直接的联系。电解液比重测量复杂,实现很困难,因此内阻法更具有实用意义,但内阻法在实际使用中仍存在限制。
(3)电压测量法(开路电压法)
开路电压与电池容量之间有较好的线性关系,用开路电压判断剩余电量具有一定的精度。但为了使开路电压尽可能逼近电池的电动势,其前提条件是电池必须经过一定时间的静置。
(4)BP神经元网络法
由于人工神经元网络的兴起,利用神经网络技术对电量的预测也逐渐成熟起来,其主要原理是将电池放电电压、电流、温度以及更多能测到的参数作为神经网络的输入,以放出的电量与总量的比值 (SOC)作为神经网络的输出(或者增加附加的需要输出量)[1]。
1.2 电池荷电状态SOC理论
电池的荷电状态(SOC)被用来反映电池的剩余容量状况,这是目前国内外比较统一的认识,其数值定义为电池剩余容量占电池容量的比值。
第一定义,恒流下的SOC:
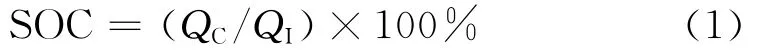
式中,QC为电池剩余的容量 ;QI为电池以恒定电流I放电时所具有的容量。
如果用已放出的电量Q来求SOC,可表示为

式中,SOC=1表示电池为充满电时的状态;SOC=0则表示电池已处于全放电状态。
第二定义,变电流下的SOC,将放电过程细分为若干个Δt,就有:
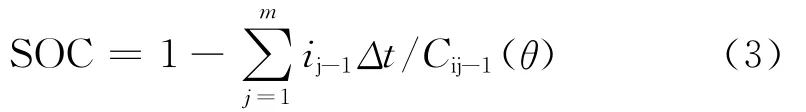
式中,ij-1表示tj-1时刻的放电电流;Cij-1表示当电池充满电时,在θ温度下,以ij-1的恒流放电所具有的容量[2]。
通常,SOC分为第一定义和第二定义。但不论是哪一种定义在实际工况中都会出现认识上的模糊。第一定义以电池在某一指定的恒流放电所具有的容量为比较基准,显然也只能描述指定恒流放电工况的电池荷电状态,否则就会出现矛盾。第二定义是在变电流放电工况下,虽然考虑了各个阶段放电电流的不同,但将表示不同恒流放电过程的SOC值相加是无意义的,并且也是会出现矛盾的结果。
2 电池荷电状态复合估算方法及其实现过程
对于SOC定义出现认识的模糊,可以通过满电量重新定义来解决。目前,在所有进行电池电量预测研究中都对电池充满电量(即满电量)状态进行了必要的修改。一般认为在标准的指定电流(A=C/n,n为整数(<10),C是电池公称容量)下能够到达过放电的终止电压(out-of-voltage)之前所能放出的电量就是满电量,或者是额定容量[2,3]。
为防止EV的动力电池可能在任何一个SOC时开始工作,而造成对安时法计量的不良影响。用开路电压法估计动力电池初始的剩余容量,考虑到恢复效应对开路电压的影响,又定义了表征自恢复效应是否结束的常数Kr。但由于在电动汽车运行中负载是变化的,放电电流是时变电流,而对同一只动力电池,用安时法进行计量时,如果放电电流不同,将放出不同的电量值,因此在电流为时变电流时必须对测得的电量值加以修正,并以标准放电电流为参照,把变电流下所得电量折算为标准放电电流的电量。于是引入了Peukert方程,它反映了蓄电池容量随负载变化的关系[4]。
确定实际电池的荷电状态值按下式计算:
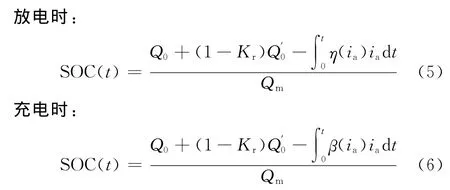
式中,Qm为电池的满容量;Q0表示在t0时刻开路电压对应的初始荷电量;Q′0表示电池在上次停止充放电时的荷电量;Kr表征自恢复效应是否结束的常数,1表示已结束,0表示未结束;η(ia)折算系数;β(ia)为蓄电池的充电效率。
在确定的SOC估算策略中,保留了开路电压法和Ah法,还采用了卡尔曼滤波进行动态精确估计,同时结合了直接调用SOC记录的方法,提出了一种复合估算策略。
2.1 电池使用之前预估算电池的初始SOC
由先验知识可知,电池初始容量Q0和开路电压U数学模型简单,可认为是静态回归模型。通过最小二乘法的一些简单方法来建立数学模型,同时用假设检验进行模型结构验证,在MATLAB中进行编程求解。
通过最小二乘法和假设检验,在稳态线性模型中的应用,安排实验进行参数估计和参数显著性检验如图1和图2。
图中“○”是实验数据,实线为一元一次模型,虚线为一元二次模型。一元一次模型的拟合质量指标R2=0.993;一元二次模型的拟合质量指标R2=0.997,但是一元二次模型中的二次项系数并不显著[5]。
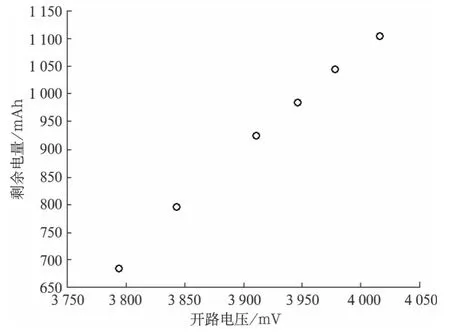
图1 实验所记录的开路电压与剩余电量
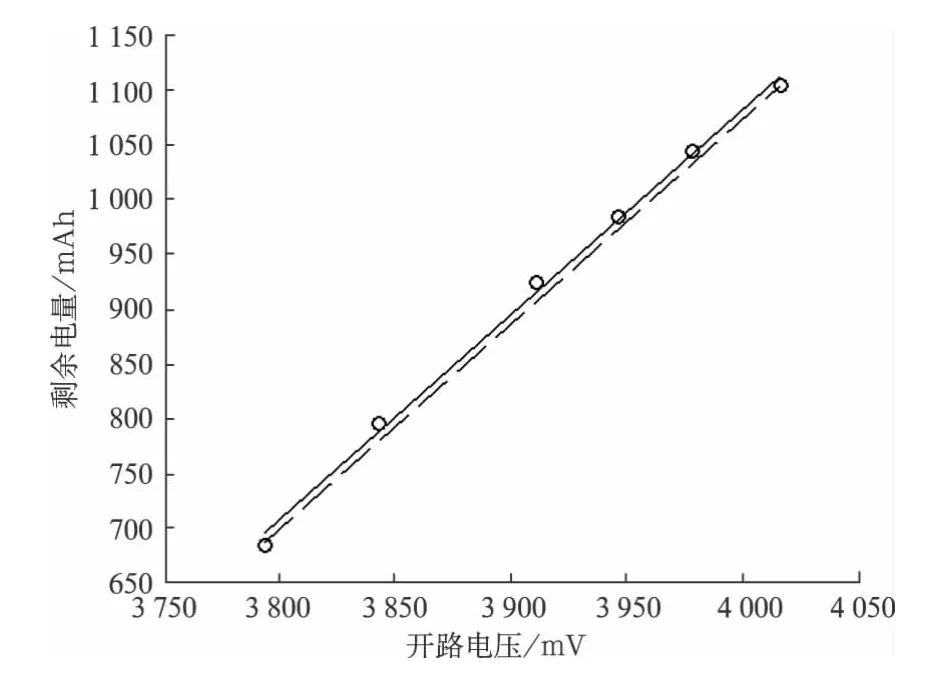
图2 两种模型的辩识结果
2.2 电池在使用过程中对电量做动态计量
电池SOC估测系统的离散数学模型:先讨论放电时的卡尔曼滤波算法,充电时用β代替即可,采用零阶保持采样离散后得:
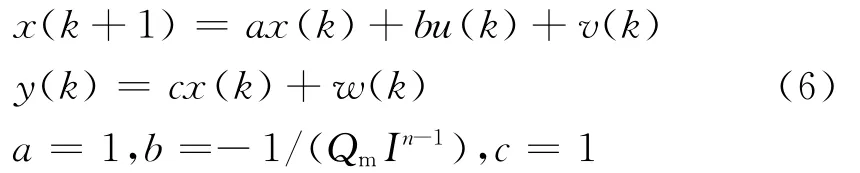
现假定v(k)与w(k)是均值为零,互不相关的高斯白噪声:
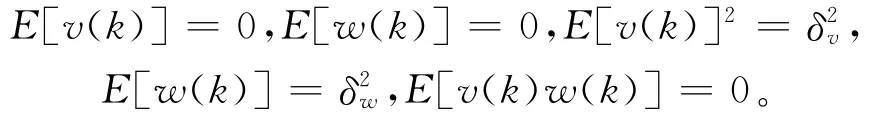
系统状态的卡尔曼滤波估计递推算法[6]:对SOC估计分为两步,一步是两个采样周期之间的状态转移,这个阶段叫做TU(Time Update)阶段:

3 结果与分析
利用MATLAB对系统进行仿真验证并且得到很好效果,系统结构框图如图3。
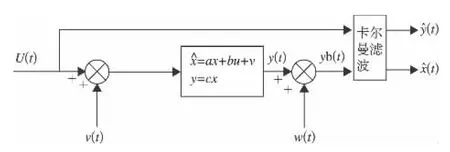
图3 系统结构框图
卡尔曼滤波器可以根据输入信号u(t)和测量输出yb(t)估计过程输出y(t)和状态变量x(t)。需要先验知识包括噪声v(t),w(t)的方差,以及如果不为零时它们的相关性,这些数据可根据实验获得。现在假设动力电池的初始容量为100 Ah,放电电流10 A,η(i)折算系数为0.984,v(t),w(t)的方差分别为0.5与1,且不相关,在MATLAB中编程仿真所得结果如图4、图5所示。
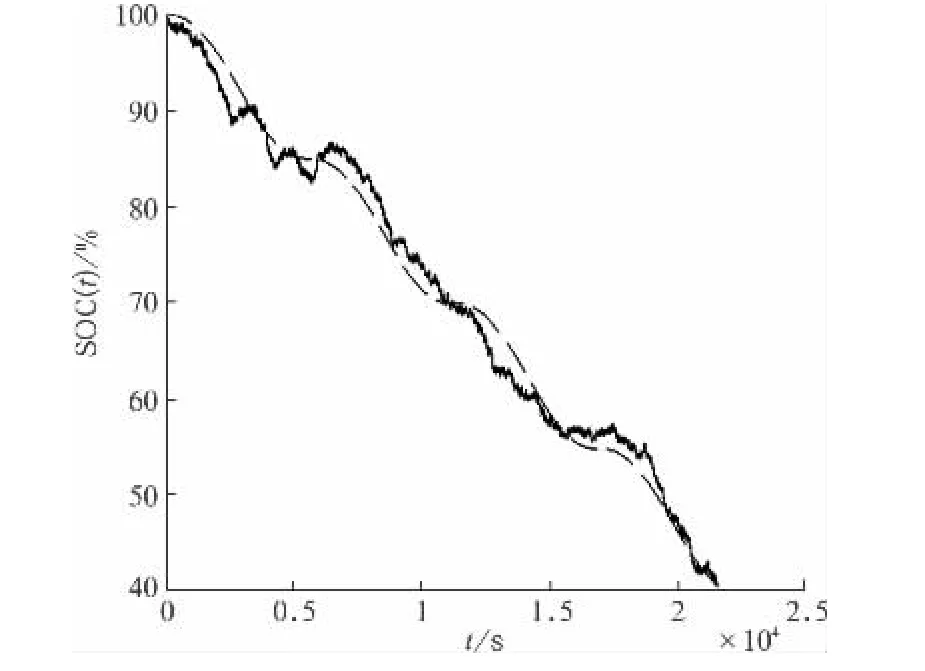
图4 系统噪声和量测噪声时的SOC
图中虚线为SOC理论输出值。最后卡尔曼滤波器的增益K(k)趋于一定值K=0.5,均方估计误差也趋于一定值P=0.5,这时可以用K近似代替稳态卡尔曼滤波器:
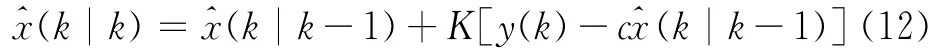
对于从有限初始时刻t0=1开始的卡尔曼滤波器式(9)而言,稳态卡尔曼滤波器式(12)不是最优的,因为其增益K不是最优增益K(t),但由于当t→∞有K(t)→K,故式(12)是渐进最优的。
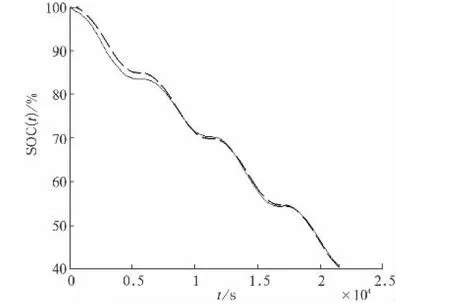
图5 SOC的卡尔曼滤波估计
4 结 论
在对电池外部特性参数的分析和对已有估算方法与估算模型进行总结的基础上,本文提出了一种基于开路电压法和安时法复合的估算方法,同时采用卡尔曼滤波方法来提高精度。该方法不仅解决了电池荷电状态(SOC)认识上的模糊,而且还阐释了模型确立过程。通过实验仿真可以看出,本文提出的模型基本上实现了电池荷电状态(SOC)的精确估算,同时对工程应用具有指导意义。
[1] 刘成尧.电动汽车用锌空电池的电量预测及管理系统的研究[D].杭州:浙江大学,2004.
[2] 高瑞昌.电动汽车能量管理系统的研究[D].北京:北京科技大学,2004.
[3] 麻友良,陈全世,朱 元.变电流下的电池荷电状态SOC定义方法探讨[J].电池,2001,31(1):7-9.
[4] 宫学庚,刘铂金,刘有兵,等.电动汽车动力电池模型和SOC估算策略[J].电源技术,2005,(10):633-636.
[5] 吴广玉.系统辩识与自适应控制[D].哈尔滨:哈尔滨工业大学,1984.
[6] 方小斌.锂离子电池在线监测系统的研究与实现[D].哈尔滨:哈尔滨理工大学,2008.

