基于改进的黄金分割法的MPPT算法研究

宋国翠，龙涛元

（中山火炬职业技术学院，广东 中山528436）

在光照强度和环境温度一定时，光伏电池输出功率随电压的变化成单峰曲线，只有在某一电压下才能输出最大功率，这时光伏阵列的工作点称之为最大功率点。为了提高发电效率，常采用最大功率跟踪（MPPT）控制［1］。常用的 MPPT方法有恒定电压法［2］、扰动观察法［3－4］、电导增量法［5］等。恒定电压法是当温度一定时，在不同的日照强度下保持阵列的输出端电压U为常数，即可大致保证阵列输出在该温度下的最大功率。该算法简单，却忽略了温度变化的影响。扰动观察法是测量当前阵列输出功率，然后在原输出电压上增加一个小电压分量扰动后，测量出改变后的输出功率，得到功率变化的方向。该算法测量参数少、容易实现，广泛应用于光伏电池的最大功率点跟踪。其缺点是到达最大功率点附近后，会在其左右振荡，造成能量损耗，尤其在气候条件变化缓慢时，情况更为严重。电导增量法通过判断工作点电压与最大功率点电压的关系可以比较精确地实现最大功率跟踪控制，但这种方法实现起来相对复杂，对硬件要求较高。基于以上各控制方法的优缺点，本文提出了改进的黄金分割搜索法，可以快速精确地找到最大功率点，并在Matlab上进行建模与仿真，验证了该算法的有效性。

1 光伏电池的通用仿真模型

1．1 光伏电池的等效电路

太阳能光伏电池的等效电路如图1所示，电气特性如式（1）［6］。

式中，IL为光伏电池板的输出电流（A）；Uoc为光伏电池板的输出电压 （V）；q为一个电子所含的电荷量，1．6×10－19C；k为波尔兹曼常数，0．86×10－4cV／K；T为光伏电池板表面温度（T＝t＋273K），单位为K；A为光伏电池板的理想因素，（A＝1～5）；Io为光伏电池板的逆向饱和电流；Iph为光伏电池板所产生的光电流，随日照强度和大气温度而改变；Rs为材料内部等效串联电阻，通常情况下Rs的值很小，在简化分析时可忽略。

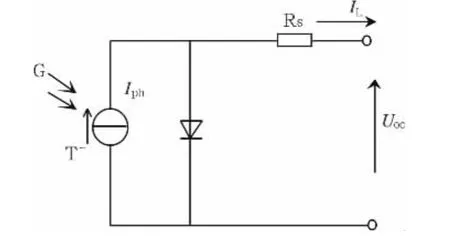
图1 光伏电池的等效电路

根据光伏电池厂提供的Uoc、Io、Um、Im等参数就可以确定该光伏电池的输出特性，需要注意厂商提供的这些参数一般是在标准温度（Tref＝25℃）和标准日照功率（Sref＝1 000 W／m2）下的测试结果。根据式（1）在Matlab中搭建了光伏电池的仿真模型如图2。

图2 光伏电池仿真模型

1．2 光伏电池的输出特性

通过Matlab／Simulink建立光伏电池模型，将光照强度和温度作为变化量输入到模型中，光伏电池的固定参数如开路电压Uoc、短路电流Isc由厂家提供的参数作为已知量输入，仿真得到不同温度下和不同光照下光伏电池的电压与功率的特性曲线，如图3、图4所示。从仿真图可以看出光伏电池的电压与功率曲线具有明显的非线性特性，当光照强度和温度一定时存在唯一的一条曲线，即最大功率点（MPP）。

2 改进的黄金分割法

2．1 黄金分割法基本思想

黄金分割法［7］是在一元单峰函数所定义的区间上按黄金分割率对称取得一系列的黄金分割点，然后对分割点所对应的函数值进行计算和比较，利用区间缩小的序列消去原理，最终确定函数的最优解和对应的最优值。具体步骤是：在区间［Ua，Ub］内取点：U1＝Ua＋0．382（Ub－Ua），U2＝Ua＋0．618（Ub－Ua），U1和U2把［Ua，Ub］分为三段［8］。（1）如果P（U1）＜P（U2），那么P（U2）是极大值，在U的定义域中，从U1至其右边到Ub可以消除，为此，在下一轮中，U1变成了新的Ub。（2）如果P（U1）＞P（U2），那么P（U1）是极大值，在U的定义域中，从U2至其左边到Ua可以消除，为此，在下一轮中，U2变成了新的Ua。因为［Ua，Ub］为单峰区间，这样每次可将搜索区间缩小0．618倍，处理后的区间都将包含极大值点的区间缩小，然后在保留下来的区间上作同样的处理，如此迭代下去，将使搜索区［Ua，Ub］逐步缩小，直到满足预先给定的精度时，即获得一维优化问题的近似最优解。黄金分割法具有均匀的收敛速度，但每次迭代时只能使给定的搜索区间从单侧进行收缩，使得其收敛速度较慢，区间缩短率偏低。虽然适当提高插值多项式的次数，如二次插值等方法可以提高计算的精确度，但次数越高，计算越繁，积累误差就越大，曲线就会出现过多的扭摆。当局部插值点有微小变动时，就可能引起曲线大幅度的变化，使计算很不稳定。因此，基于以上算法的优缺点，本文提出一种改进黄金分割法，采用此法进行最大功率跟踪。

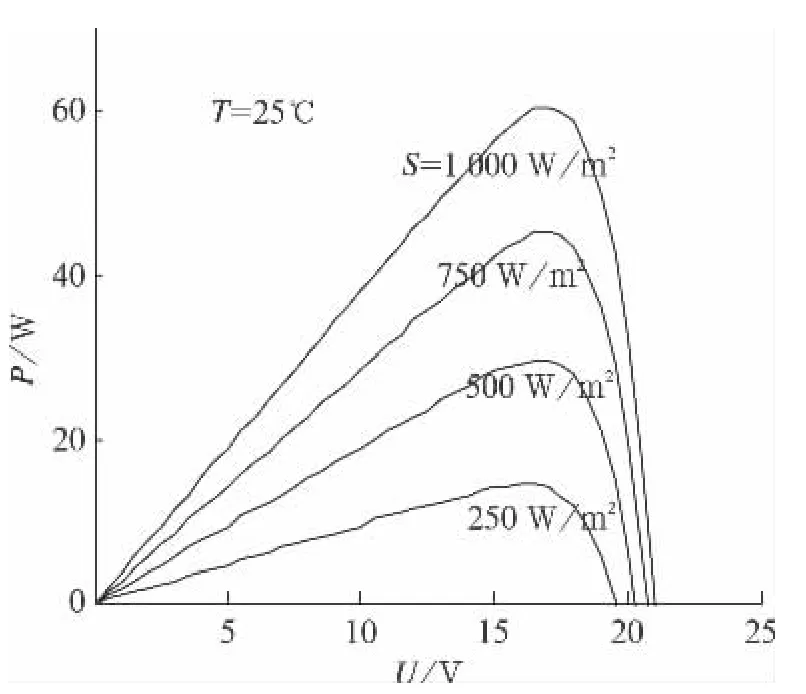
图3 不同光照对P－U曲线的影响

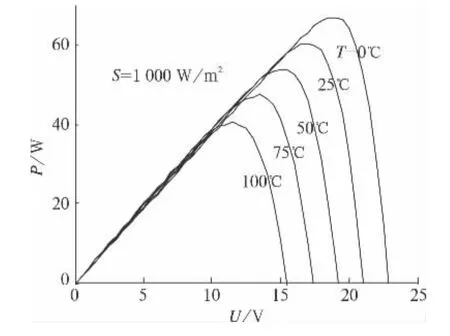
图4 不同温度对P－U曲线的影响

2．2 改进的黄金分割法

改进的黄金分割法控制流程图如图5所示。

利用黄金分割法可靠的优点，尽可能地缩小黄金分割地搜索区间，提高搜索速度。大体设计思路根据光伏电池温度一定时，光伏电池的输出P－U曲线上最大功率点电压几乎分布在一个固定电压值（0．78Uoc）两侧的情况，以0．78Uoc作为搜索起点，通过加减步长的方法在附近找到两个电压点分别作为黄金分割法的上边界点和下边界点，而让最大功率点的电压落在该区间内，那么再进行黄金分割算法进行寻优，便可以很快找到最大功率跟踪点。

首先基于光伏电池MPP处的电压约为开路电压的0．78倍［9］，因此可将系统开路电压乘以0．78作为CVT启动指令电压值。控制光伏电池的输出电压从开路电压开始下降，往最大功率点电压方向移动。当系统输出电压达到指令电压后，测量功率P1，调整输出电压，测量当前的电压U、电流I，并计算功率得到P2。通过比较判断P1和P2的大小从而判断P1、P2点在极大值的左边还是右边，如果是左边加步长得U2，判断是否满足选取的点在最大功率点的右边，如果满足则继续执行，如果不满足则继续增加步长，直到满足选取的点在最大功率点的右边为止，从而确定黄金分割的区域；如果在右边则减小步长，然后进一步使用黄金分割。

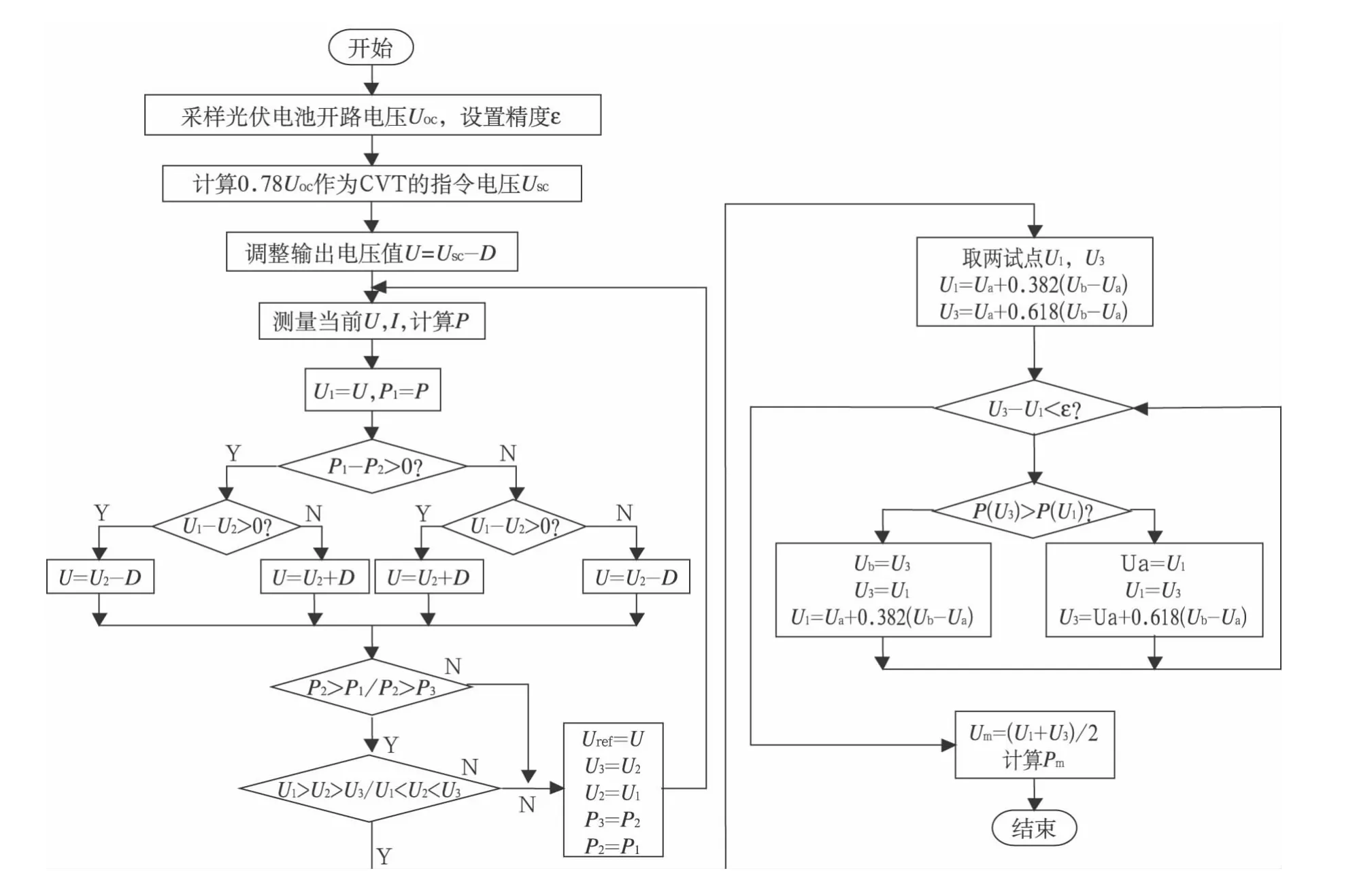
图5 控制流程图

3 仿真验证

搭建Boost电路，以占空比为实际控制量，实现迭代收敛算法。模拟环境改变的情景，在0～1 s时光照强度 为1 000 W／m2；1～2 s时，光 照 强 度 下 降 为800 W／m2；在2～3 s时，光照强度下降为760 W／m2，如图6所示。扰动情况下，电压随光照强度变化的仿真结果如图7所示，功率随光照强度变化的仿真结果如图8所示。在相同精度的情况下，通过与原始的黄金分割法进行对比，改进的黄金分割算法迭代次数明显小于后者。根据仿真结果可以发现，基于改进的黄金分割搜索法具有较高的控制精度，较快的收敛速度，而且具有良好的稳定性。

图6 光照强度变化曲线

图7 电压跟踪曲线

图8 最大功率跟踪曲线

4 结束语

为了提高太阳能电池的利用率，将改进的黄金分割法应用在太阳能电池最大功率跟踪上，通过仿真实验很好地证明了该方法的可行性，实现了MPPT控制，减少了因环境变化造成的功率损失，改善了传统扰动法在最大功率点附近左右振荡的问题，为MPPT提供了新的解决思路。

［1］ 邱培春，葛宝明，毕大强．基于扰动观察和二次插值的光伏发电最大功率跟踪控制［J］．电力系统保护与控制，2011，（2）：62－67．

［2］ 韩 伟，王宏华，贾艳刚．改进黄金分割法在光伏发电MPPT中的应用［J］．电源技术，2014，（2）：282－285．

［3］ Esram T，Chapman P L．Comparison of photovoltaic array maximum power point tracking techniques［J］．IEEE Transacti－ons on Energy Conversion，2007，22（2）：439－499．

［4］ Jung Youngseok，So Junghun，Yu Gwonjong，etal．Improved perturbation and observation method（IP＆O）of MPPT control for photovoltaic power systems．IEEE E－lectron Device Society［C］．Conference Record of the IEEE Photovoltaic Specialists Conference，2005，Lake Buena Vista，FL，United states．Institute of Electrical and Electronics Engineers Inc：2005．

［5］ 孙自勇，宇 航，严干贵，等．基于PSCAD的光伏阵列和MPPT控制器的仿真模型［J］．电力系统保护与控制，2009，37（19）：61－64．

［6］ Walker，G．Evaluating MPPT converter topologies using a matlab PV model［J］．Journal of Electrical ＆ Electronics Engineering Australia，2001，21（1）：49－55．

［7］ 宋巨龙，钱富才．基于黄金分割的全局最优化方法［J］．计算机工程与应用，2005，（4）：94－95．

［8］ （美）Steven C Chapra．工程与科学数值方法的 Matlab实现［M］．北京：清华大学出版社，2009，（5）：179－184．

［9］ 徐鹏威，刘 飞，刘邦银，等．几种光伏系统MPPT方法的分析比较及改进［J］．电力电子技术，2007，（5）：3－5．