船体变形对主机轴承负荷影响的近似计算

李百艳，张 宇，陈椿芳

（大连船用柴油机有限公司，大连 116021）

0 引 言

船舶机舱双层底变形对轴系校中的影响，自20世纪70年代开始就一直受到各船级社及从事船舶设计和建造的研究部门所重视。其原因是在一些营运船舶中曾出现过主机倒数第二道轴承（EB2）或倒数第三道轴承（EB3）受船体变形影响失去负荷而造成轴瓦损坏的事故。为此，NK船级社在对上述事故船舶进行了大量的分析研究工作后，给出了基于船体变形对主机轴承负荷变化影响的近似计算方法[1]。该计算方法现已作为入级NK的船舶及其推进系统轴系校中的补充验证工具而推广应用。

1 船体相对位移的近似计算

在设计主机将被安装在预先确定的基准线之下的船用推进系统时，通常采用的是倾斜校中。当该轴系因船舶吃水提高而发生船体变形时，每个轴承与其他轴承的相对位置亦将发生变化（见如图1（a））。

精确地确定这些位置变化对于确定轴承及轴系最为适宜的对中将起到直接的作用。因此，理想的就是确定从船舶轻吃水的初始状态到满吃水变形后所发生的位置或位移的相对差别。得到的相对位移以轴系在船体支承结构变形前的状态为基础，并且假定主机轴系部分（曲轴）的相对位移可忽略不计（见图1（b））。将初始状态设置为基准线并据此测量产生于满吃水状态的相对位移是很有用的。主机之后的船体相对位移δ的近似计算是使用X-Y坐标系统，其中主机最后一道主轴承（EB1）被规定为坐标系的原点（见图 1（b））。在此假定，主机之后每个轴承位移的变化与船体支承结构相关部位的位移相对应。

由EB1轴承到机舱最后舱壁的轴系长度上的相对位移δ可采用FEM（有限元）法分析，该位移大致与X的n次方成比例。利用这样一种关系可有助于简化确定某一校中相对位移的过程。

图2表示FEM分析与若干具有不同n值的Xn曲线计算结果之间的比较，涉及某一300000dwt油轮从EB1轴承到机舱最后舱壁轴系的相对位移。该图显示n为1.5时给出相对位移的最佳近似。类似结果在其他船舶上亦可见。因此，就认为从EB1轴承到机舱最后舱壁轴系所对应的船体支承部位的相对位移可以用X1.5近似表示。

图1 由船体变形引起的轴承位移变化

在机舱最后舱壁以后的船体结构包括一个高刚性的艉管支座，由此可将该部位的位移变化近似为线性。这样一来，机舱最后舱壁以后的艉管轴承的位移变化可以由X1.5指数曲线在后舱壁处的切线给出。根据该近似方法，由船舶吃水提高而引起的船体相对位移δ可以表示为式（1）。图3表示用以确定因船体相对位移引起的主机之后各个轴承位移变化的计算模型：

式（1）中：X——与EB1轴承支点的距离（mm）；L——EB1轴承支点到机舱最后舱壁的距离（mm）；δB——机舱最后舱壁处的相对位移（mm）。

图2 FEM分析与若干Xn曲线之间的比较

图3 用于计算主机最后主轴承以后各轴承位移变化的相对位移模型

2 由相对位移模型确定的支反力影响数

支反力影响数通常在船用推进轴系的校中计算时使用。它被定义为显示当某一特定轴承的位移变化一个给定的单位值时，其自身或其它轴承支反力相应变化的程度。例如，当轴系的1～4号支点的位移改变时，6号支点处支反力的改变量ΔR6可以用支反力影响数Cm,n表示（见图4（a））：

式（2）中：δn——支承点位移n的变化量；Cm,n——当支承点n向下移动1mm时支承点m处支反力的变化量（支反力影响数）。

式（2）可以用在以上内容中所描述的船体相对位移的模型更新。其原因在于 1～4号支承点位移的变化是由式（1）得到的。也就是说，式（2）可以按照如下用δB和xn来取代，这里xn是从支点5号（EB1轴承）到支点n号的距离。

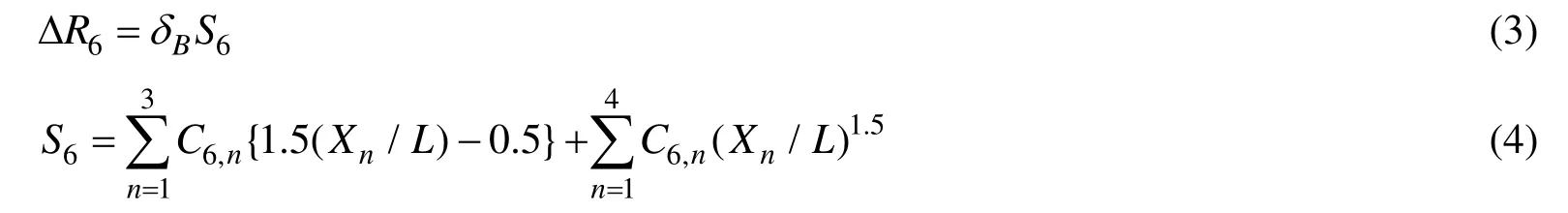
既然δB和δn两者都表示相对位移，而S6亦表示与支反力影响数C6,n(n=1～4)相同的含义（见图4(b)），如果假定所有支承点的相对位移δn可以用机舱最后舱壁处船体的相对位移δB来替代，S6就可以被考虑为反映出各支反力影响数C6,n(n=1～4)对某一支点综合作用的当量支反力影响数。

图4 利用支反力影响数计算轴承的支反力

假定Si是在机舱最后舱壁处船体向下位移1mm时，第i个主机轴承（从后数起）处支反力的增量：

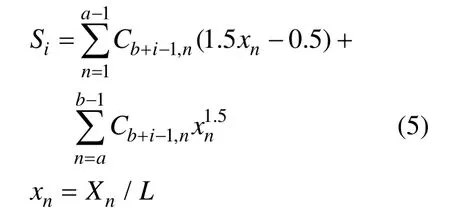
式（5）中：n——支承点的编号（从轴系后端计数）；a——机舱最后舱壁最前面一个支承点的编号（从轴系后端计数）；b——EB1轴承的编号（从轴系后端计数）；Xn——从支承点b到支承点n的距离；L——从支承点b到机舱最后舱壁的距离；Cm,n——当支承点n向下位移1mm时，支承点m处支反力的增量（支反力影响数）。

在式（5）中，应注意Si的下标i表示从主机后端计数的轴承编号。式（4）内的S6与式（5）内的S2（i=2）对应，而a和b分别与4和5对应。

3 使主机轴承失去负荷的船体变形

利用支反力影响数Si并结合船体的变形，可以确定能引起主机第i个轴承失去负荷的船体相对位移量。这里，有两种轴承的支承情况被用于计算支反力影响数Cm,n，即，弹性支承（弹簧支点）或刚性支承（简支）。

3.1 弹性支承

在这种情况下，使主机轴承失去负荷的船体相对位移δB可用简单的方法计算。先设Ri为船体变形前的主机第i个轴承（从后计数）的支反力并设δBi为主机第i个轴承失去负荷时机舱最后舱壁处船体的相对位移，则：

既然在大多数情况下，由于船体变形而引起的主机轴承失去负荷仅限于EB2和EB3轴承，则δB2和δB3均应计算且其较小值应与NK给出的低限值进行比较。

3.2 刚性支承

图5表示如何处理船体变形前状态下主机轴承座的刚度。当在计算中考虑刚性支座的情况时，对于每一个轴承都能够很容易地得到与给定的位移相对应的轴承支反力Ri以及如图5(a)所示的由该支反力为零而引起的支点位移。但是，如果在这里考虑了刚性（弹簧）的作用（见图5(b)），支承点事实上将随负荷少许向下移动，而这实际就包括了每个轴承的轴承支反力Ri的变化。

图5 主机轴承初始状态

假定支反力Ri即使在考虑刚性（弹簧）作用时亦不变化，各支点加载后的位移用各支点不变的刚度K，则表述为：

下面讨论船体由于吃水提高而从图5(b)所示的初始状态发生变形时轴承支反力的变化。图6表示在发生船体变形前与变形后支点（与轴的接触点）的变化。由图6可知，这里可以假定所示支点垂向位置的变化并不是由主机以下部位船体结构的变形引起的，而是由起因于轴承负荷提高而致使机座变形所引起的。

图6 由于机座弹性变形引起的支承点位移

为了使用基于刚性支座的支反力影响数来得到船体变形后的轴承支反力，对特定条件下求解包括以支点的支反力及位移：

式（8）中：i——从主机后端计数的主机轴承编号；Ri——船体变形前支点i（从主机后端计数）的支反力；Ri'——船体变形后支点i（从主机后端计数）的支反力；δi——支点i（从主机后端计数）的弹性变形位移；Ci,j——当支点j向下移动1mm时，支点i处（从主机后端计数的支点）支反力的增量（支反力影响数）（注意式（8）中下标的含义与式（2）的不同）

式（8）可以重写为：

在式（10）中，考虑船体变形后EB2轴承失去负荷的情况，则：

这表明EB2轴承的支点由于船体变形前的轴承负荷R2回复到初始状态而向上移动了位移h2，换言之，此时弹簧的恢复力应为零。

设引起EB2轴承失去负荷的相对位移为δB2，然后，求解以下带有5个变量δB2，δ1，δ3，δ4和δ5的联立方程以便得到δB2，这里δ2不是变量。

式（12）中：K=5000kN/mm为常量。

图7表示船体变形前后，轴系及主机轴承相对位移的状态。

图7 考虑主机轴承刚性时支承点的支反力与位移

式（12）可以用矩阵的形式表达：

式（13）中：

4 计算实例

以某一57000t化学成品油轮的轴系校中计算书[2]为例，从该校中计算书所提供的有关数据计算出用于判断是否能使EB2和EB3轴承失去负荷的δB2和δB3值。

图8和表1分别表示轴系布置的简要尺寸以及从轴系校中计算书中得到的支反力影响数，表2为各轴承的支反力和位移。

4.1 几点说明

在原校中计算书中，艉管后轴承仅取一个支点，并且取消了艉管前轴承。因此，在图8中，SB1与SB2距离为零即表示已将两个支点作为一个考虑，而SB2与SB3（艉管前轴承）距离为零则表示已取消艉管前轴承。这里规定表2中所列出的支反力向上方向为正，而位移向下方向为正。

将式（1）～（14）用电子表格的形式编制一个简单的计算程序，并输入有关数据进行计算。

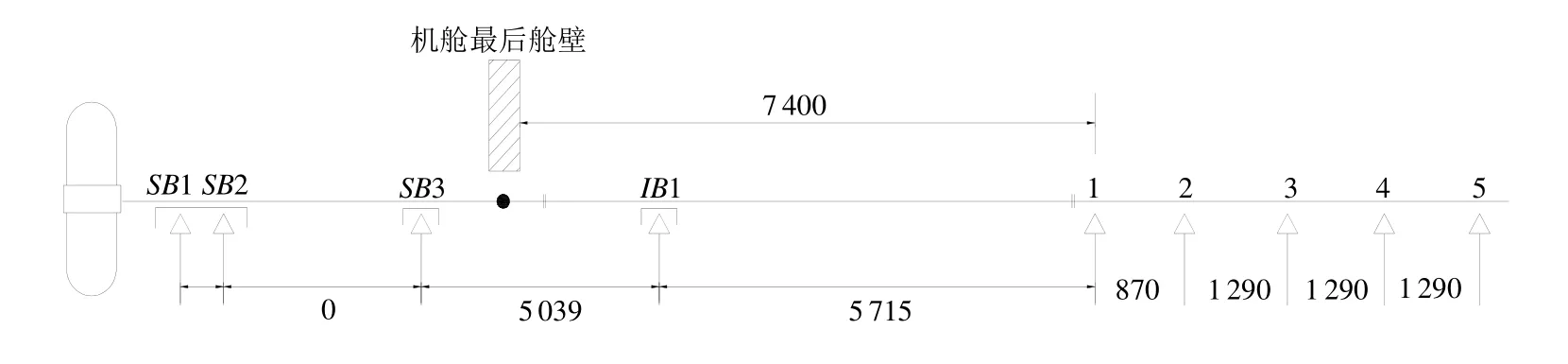
图8 轴系布置及尺寸

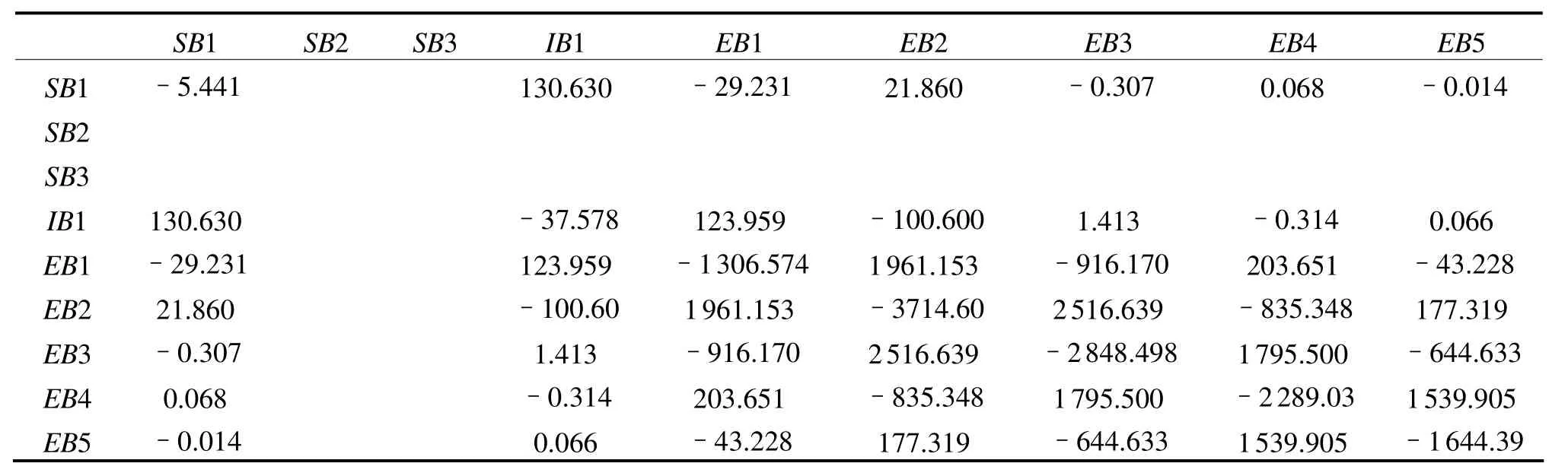
表1 支反力影响数 单位：kN/mm

表2 轴承支反力与位移（热态）

4.2 计算结果

表3表示Si（i=1～5）以及δB2和δB3的计算结果。由此可以看出，受到船体变形影响最大的是EB1和EB2轴承，并且当EB1轴承的负荷提高时EB2轴承的负荷将随之降低。同时，当船舶吃水增加并且机舱后舱壁处的相对位移δB2达到3.59mm时EB2轴承将首先失去负荷。具体δB2和δB3计算值与NK限制要求的关系见图9。

表 3 Si，δB2和 δB3计算结果

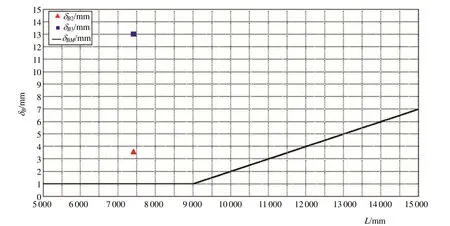
图9 δB2与允许限制的比较

图9表示了计算所得的δB2和δB3与NK允许限制的比较。在大量统计数据的基础上，NK认定当EB1轴承到机舱后舱壁的距离小于9000mm时，因船体变形引起的机舱后舱壁处的相对位移一般小于1mm。而当该距离大于9000mm时，则机舱后舱壁处的相对位移将按直线比例关系增加到7mm左右。由上图δB2和δB3点位与限制线的位置关系可以看出：本算例中，EB1轴承到机舱后舱壁的距离是7400mm，以Δ为标志的δB2值已高于NK限制线。因此，考虑船体变形影响后的EB2轴承在任何工况都可以安全工作。

此外，还有两个计算实例是分别针对某一入籍DNV船级社的300000吨级原油轮和另一入籍LR船级社的3900TEU集装箱船进行的，同样验证了上述NK计算方法的有效性。

5 结 语

在进行现代大型船舶推进轴系校中计算时，为保证EB2和EB3轴承在任何工况下（冷态、热态、船舶轻吃水、船舶满吃水）都能保持足够的负荷，通常的做法是：在冷态校中计算时，使EB1轴承的负荷尽可能的小（甚至可以为零），而使EB2和EB3轴承有比较大的负荷以抵消将来船体变形可能对两者不利的影响[3,4]。这一看似简单易行的补偿方法，实际上反映了船舶从轻吃水到满吃水状态船体变化的规律，其良好的调整效果已在很多实船上得到了验证。正是在此基础上，NK进一步对船体变形与主机轴承负荷变化之间的关系给出了非常直观的量化指标。借鉴NK提供的这一数值化的考量方法，船舶推进轴系的设计人员，能加深对轴系校中计算中涉及到的船体变形问题的理解。

[1] 2013 Guidance for the Survey and Construction of Steel Ships (Annex D6.2.13) CLASS NK[S].

[2] DMD. Shaft Alignment Calculation Report for 57000 dwt Chemical Product Oil Tanker[R].

[3] WNSD. Engine and Shafting Alignment for RTA/RT-flex Engines[R].

[4] Main Engine Alignment[R]. Diesel Technology Seminar East Asia. 2010.