大面积堆载预压对高速路桥基的影响
涂芬芬 周洪涛 田志国
(1.深圳市勘察研究院有限公司,广东深圳 518026;2.深圳市建筑设计研究总院有限公司,广东深圳 518031)
外加堆载不仅会影响淤泥表层,而且会影响深层淤泥的变形,尤其是大面积堆载,可以引起淤泥土明显的深层滑移,这在不同类型的淤泥软土中表现的有所不同:在第一类淤泥软土中(原状淤泥或淤泥质软土),堆载不仅会引起周边较近距离内土体的隆起,而且还可以引起淤泥土明显的深层滑移,这在大面积堆载中表现的尤为明显。第二类淤泥软土(有一层薄的硬壳层)首先应考虑其自身的稳定性,由于此类土体新近且已堆加荷载,如果进一步施加外力,有可能引起土层的剪切破坏。对于第三类淤泥软土(堆载时间较长,硬壳层较厚),由于物理力学性质有所提高,其变形情况要较前两类小,但如果堆载过大同样也会出现周边土体隆起和深层滑移的问题。对于堆载附近的建、构筑物基础,应注意堆载对既有建(构)筑物侧向挤压的影响。其影响范围之大,且由此产生的工程桩或桥基的水平偏移破坏亦不乏事故实例。
1 工程概况
本工程位于深圳市前海填海区,沿江高速桥基已施工完成,现在正在施工道路路面。沿江高速北侧为已经软基处理完成的中集地块,南侧为待建的F地块,西侧为堆载完成的C地块,东侧为污水处理厂。沿江高速段桥基距离F地块红线约50 m。由于F地块软基处理采用堆载预压方式,且正要施工,为了避免F地块大面积的堆载对沿江高速已建桥基造成影响,分析和研究大面积堆载对桥基造成的位移,指导现场堆载施工。
根据F地块的软基处理设计及现场实际情况,分析距离研究高速桥基50 m以外的F地块逐层加载对桥基的影响。
2 计算模型
1)土层的分布情况。计算所用土层划分为四层,人工填土层、淤泥质土层(淤泥质粉质粘土层)、砂质粘性土层和全风化花岗岩层。人工填土为素填土:杂色,由粘性土、砂砾及花岗岩质块石、碎石混杂组成,局部碎石及块石含量较高,稍密~中密。人工填土层地表变化较为复杂,地表标高由图1可知由左及右依次为5.5 m,7.0 m和3.5 m,各个不同地表标高间由1∶2斜坡过渡。填土层厚度中部最大,约为8.5 m,最薄处为5.0 m。场地堆载施加于右侧3.5 m地表及斜坡过渡处,堆土厚度8 m,分5次分别堆载施加,在计算过程中将其转换为与之相对应的均布竖向荷载加以计算。人工填土层其下为淤泥质土层,淤泥质土层由淤泥经上部人工填土的长期压缩固结形成,土层厚度为10 m,其具体分布按场地实际条件取值。淤泥质土层与基岩间为粘土、粉质粘土、砾砂和砂质粘性土,在取值时,由于砂质粘性土物理普力学参数较低,故以此层参数为主进行计算,计算层厚为20 m。基岩层由全风化和强风化花岗岩层组成,层厚10 m,在计算过程中取全风化花岗岩层参数进行分析。

图1 场地地质条件及加载图
2)桥基模型。桥墩基础为双排桩基,桩径1.8 m,纵向间距为30 m,将其简化为沿横向10 m、纵向5 m均匀分布的平面单元,用以约束土体的水平和竖向位移。其物理力学参数的取值系数为桩基横截面积与所对应土体计算面积的比值。在计算过程中,土体单元采用分段弹塑性应力—应变模型,桥墩约束单元采用线弹性单元。

图2 土体弹塑性本构模型
3)土体模型。图2中a),b),c),d)分别为人工填土、淤泥质土、砂质粘性土和全风化花岗岩土体的弹塑性本构模型。土体应力应变曲线由四段折线构成:应力为0 MPa~0.1 MPa时,应变为0~0.02;应力为0.1 MPa~0.2 MPa时,应变为0.02~0.05;应力大于0.2 MPa后的应变为0.05~0.4与大于0.4的强化弹塑性和理想弹塑性阶段。本计算过程中没有考虑F地块软基处理施工过程中淤泥的物理力学参数指标的变化,如淤泥弹性模量指标随着堆载过程的增长等。
4)计算的模型。图3为实际计算模型的单元网络划分和具体剖面尺寸,其中模型的边界约束情况为:左侧与右侧边界节点为水平约束,下侧节点为X向与Y向的双向固定约束。两侧的水平约束为考虑远场边界的边界位移不变,对于竖向变形,右侧是大型加载区,其水平面及斜坡过渡段均有大面积加载,存在一定竖向位移,故不予施加竖向约束。荷载施加按8 m厚场地堆载施加,分为5次等值加载,并考虑各分层土的弹塑性变形。计算模型底部为双向固定加载,模拟基岩对模型的约束作用。
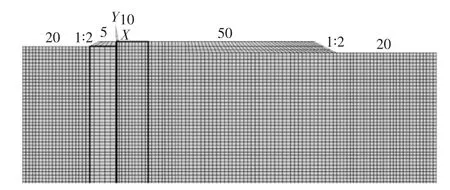
图3 土体单元计算模型(单位:m)
3 各工况计算分析结果
第5荷载步位移计算结果见图4。

图4 第5荷载步位移计算结果
4 计算结果列表
桩基单元不同深度各测点的计算结果:侧线为桩基单元体的右侧边线,即x=10 m处竖向侧线,各测点竖向位置及计算结果如表1所示。

表1 各测点的计算结果(最终荷载步)
5 结语
根据分工况计算分析,在分级加载的过程中,计算模型的大变形区域主要集中于分级荷载施加区域的右侧。对于土体水平向位移其正向(向右为正)最大值主要集中于以右侧放坡段为中心的土层表面,随着测点距坡段距离的增加而减小;土体水平向位移其负向最大值主要集中于右侧放坡段左下方,分布的深度区域为淤泥质土层和砂质粘性土层的上部。随着测点距右侧坡面和其下部土体距离的增加,竖向和水平位移均明显减小,当变形传至桩基单元处时,位移已不明显。由各个荷载步的堆载对桩基单元的影响可知,水平位移明显大于竖向位移,且两者均可满足位移变形的要求,水平位移幅值最大约为1 mm。图5为桩基单元不同深度各测点的位移随堆载增加的变形曲线。

图5 各测点位移图
由图5可知,桩基单元体的右侧竖向边缘不同深度测点的位移在竖向和水平向的位移变化趋势有所差别,但总体幅值均小于1 mm,能够满足桩基变形要求。桩基水平位移在堆载施加的前中期(1步~3步堆载),变形呈线性变化,且地表测点出现正向位移,随着荷载步的增加,桩基单元各测点的水平位移明显增加,而且地表测点的水平位移也由正值转为负值,且绝对值变化明显。竖向位移变化与水平位移不同,峰值出现在第3~第4加载步,但总体比水平位移小得多。
6 意义
为了防止由于在淤泥软土上的加载或卸载引起的基础及桥基变形及破坏现象,杜绝关乎国民经济命脉的交通、城市中心区以及重要工业建筑的安全隐患,树立党和国家在广大人民群众中的公信力,节省不必要的开支,合理运用国家税收,构建和谐社会。本文在研究成果成熟并经检验完善后,在条件允许下,可为后续类似工程提供依据及参考。
[1] Mohamedelhassan E.Shang J Q.Vacuum and surcharge combined one dimensional consolidation of clay soils[J].Canadian Geotechnical Journal,2002,39(5):1262-1264.
[2] Thomas H Dawson.Offshore Structural Engineering[M].Prentice-Hall INC,1983.
[3] Matlock H.Correlations for design of laterally loaded piles in softclay[C].Proceedings of the Offshore Technology Conference.Houston.Texas OTC,1970:544-593.
[4] 胡中雄.土力学与环境土工学[M].上海:同济大学出版社,1997.
[5] 李 凡,吴志昂,孙四平.软土地基路堤最终沉降量推算方法研究[J].合肥工业大学学报(自然科学版),2003(2):123-126.
[6] 卢世深,林亚超.桩基础的计算和分析[M].北京:人民交通出版社,1987.
[7] 徐晋英.预应力技术在公路桥梁施工中的应用研究[J].山西建筑,2012,38(7):183-185.

