基于支持向量机在重工业经济领域预测研究

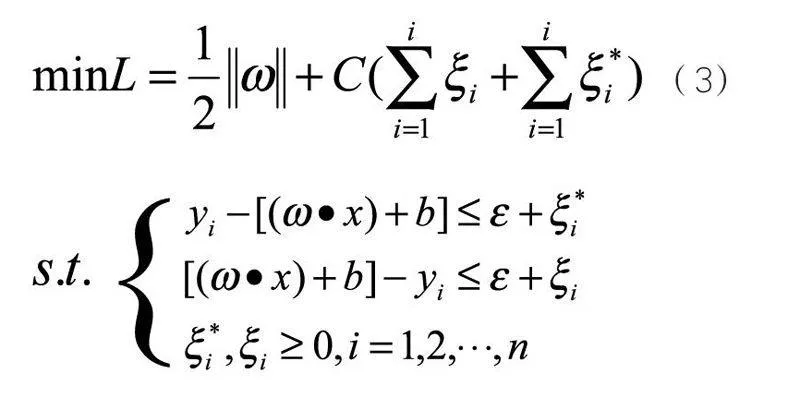
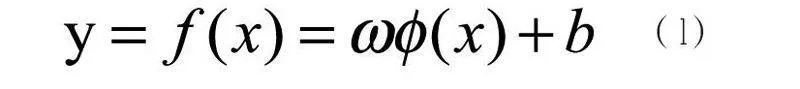
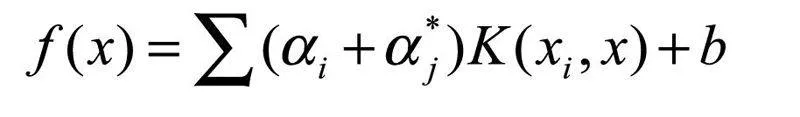
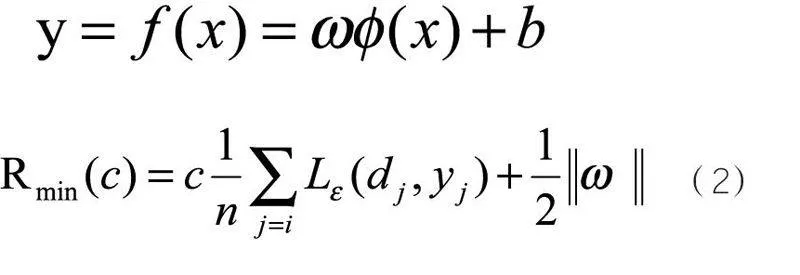
摘要： 提出了一种基于支持向量机预测重工业经济月度同比增长率的方法。利用2002年以来，我国6年的重工业月度同比增长率数据，建立支持向量机预测模型，并对预测结果和实际值进行了比较分析，表明该方法用于经济预测和经济分析是有效的。

关键词：支持向量机；重工业；经济预测

中图分类号：F201

一、引 言

重工业在我国经济发展中占有重要地位，是我国工业、特别国防工业发展的基础[1-6]。重工业发展趋势预测是一项重要而复杂的工作。准确的预测可以使政府、相关企业及其他有关部门更好地把握未来经济运行状况，从而做出有效的经济决策和发展策略。影响重工业发展的因素比较多，例如能源产能、交通物流、资本环境、环境保护以及地方政策改变等，它们之间相互影响又相互制约，最终使得重工业经济系统呈现复杂性、开放性、时态性、非线性等特点。近年来，国内外对于经济预测给出了许多方法。从预测基础体系而言，经济预测方法大体分为两类：基于历史数据预测方法和经济理论定性分析预测方法。基于历史数据预测方法主要有回归分析法、投入产出法、时间序列分析法、遗传算法、动态规划法等；经济理论定性分析预测方法有：层次分析法、市场调查法、销售人员估计法等。此外科研工作者亦开发了多种基于上述方法组合和改进的预测方法。然而，由于经济发展越来越趋于全球化和多维性，现代重工业经济发展已经是一种综合性发展，传统预测方法已经满足不了实际预测需求，需要一种兼顾历史数据内部关系及经济基础理论的方法才能够进行准确地预测。

支持向量机（SVM）最早发展于分类，20世纪90年代Vapnik等将支持向量机首次应用于回归问题，是一种介于定量预测与定性分析之间的分类预测方法，在解决小样本、高维度及非线性问题上优势明显[7]。SVM方法在许多领域已经取得了广泛应用，例如在指纹识别、人脸识别、字符识别、手写识别等[8][9][10]，SVM算法在准确性上已经于传统的学习方法不分上下。其缺点也很明显，对于大规模数据处理效率较低，运算时间较长。

本文利用支持向量机能够同时进行定量和定性处理非线性问题上的优势，较好地进行了非线性经济预测。 利用支持向量机方法分析历史数据，预测重工业同比月增长率，理论预测结果与实际值符合较好。从而从一定程度上说明了支持向量机用于重工业领域经济预测是有效可行的。

二、基础理论及模型

SVM理论基础及预测模型分析如下：

（一） SVM理论基础

SVM函数预测，基本思想是通过一个非线性映射，把输入空间的数据映射到高维特征空间中，在高维特征空间中构造线性回归函数实现原空间中的非线性回归问题，最终做出预测。具体算式如下：

算式中系数ω和b可以由下式来估计求得：

（二） SVM预测模型

通常给定数据点集 ，其中 xi是输入向量，di是期望值，n为数据总数。建立SVM预测模型，实际上，SVM预测也就是方程 的求解过程。根据相关数学理论，转换为如下最优化问题：

引入拉格朗日乘子和核函数后，得到支持向量回归函数：

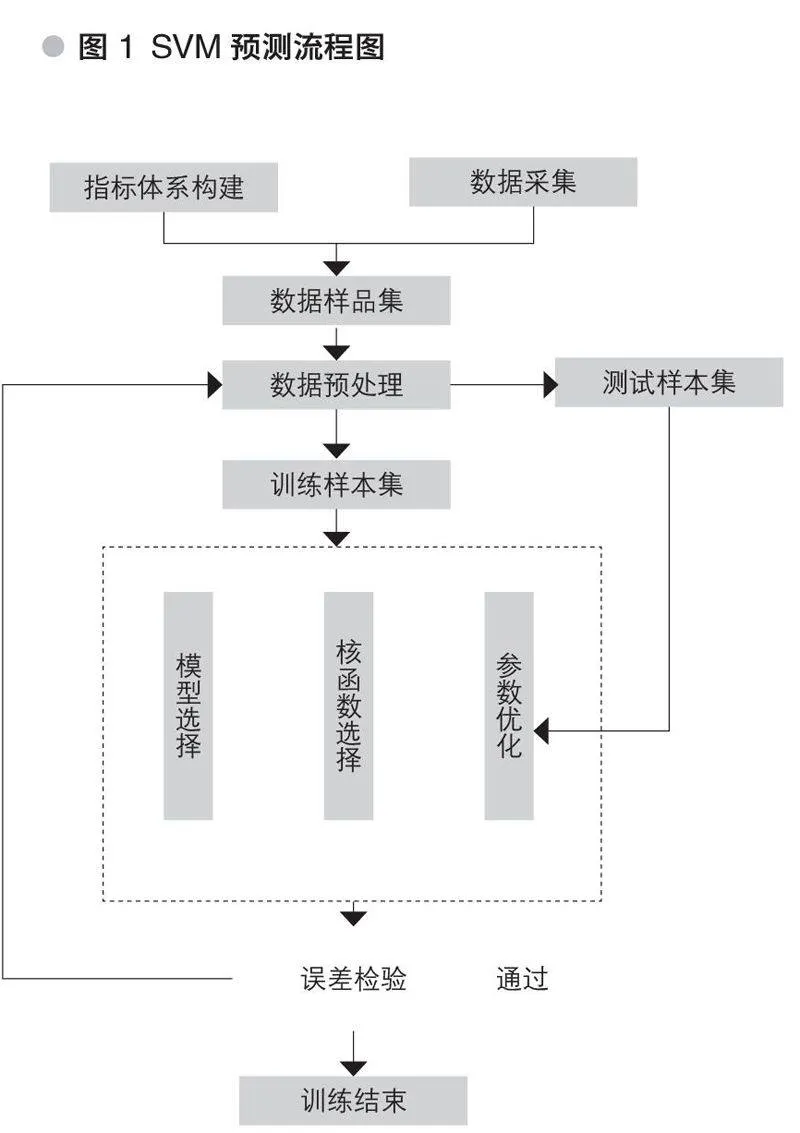
具体而言采用SVM进行预测的一般运算流程如图1所示：

三、基于SVM重工业经济预测研究

本部分主要介绍了传统重工业经济预测模型、指标体系构建及数据准备、预测过程、预测结果及分析。

（一） 传统重工业经济预测模型

传统重工业经济预测模型包括如下几种，分别是：

1.经济计量模型

以宏观经济学理论为基础建立模型，根据给定的外部变量以及宏观政策变量预测相关经济量。该模型对于季度、月度预测效果较好，且应用时间广，但是存在方程组过多运算量巨大，历史数据质量不高的缺点。

2.决策树法

利用贝叶斯原理，根据每一可能事件给定概率进行预测。由于事件概率均为人工给定，受人主观影响干扰较大；且一旦出现未能预估事件，预测结果往往与实际相差甚远。

3.回归分析方法

在长期观察历史发展规律基础上，分析各种经济现象关系，建立模型来分析预测的方法。重点在于解释各变量之间的关系，而并不是对于经济进行短期、长期预测。

4.投入产出模型

投入产出模型是基于研究和分析产业部门之间产品和消耗之间的数量依存关系进行预测的方法。此种方法应用于产业部门较多，对于宏观经济而言，不存在特定的产品和消耗之间的直接制约关系，因此在宏观经济领域应用具有局限性。

5.销售人员估计法

销售人员估计法是将营销网络各级销售预测值自上而下加和统计进行预测的方法。其受销售人员主观影响较大，销售人员往往为了自身利益会对于数据进行一定处理，加和统计数据误差较大，数据可信度不高。

6.时间序列模型

此方法不以经济理论为依据，根据历史数据自身变化规律利用外推机制来描述时间序列的变化。其存在理想假设过多，受经济社会结构影响较大的弊端。

7.专家预测法

将营销、生产、财务等多方面专家联合起来，结合其工作经验和直觉进行预测。此种方法如采取模糊数学进行处理，预测效果较好，但人为主观性较大，且耗费人力物力巨大，成本过高。

上述为常见重工业经济预测的一些方法，优势明显也有一定的弊端。支持向量机是基于结构最小化原理，通过一个二次规划方法，获得了较高的性能。众多学者将其推广到经济预测领域，并取得了较好的效果。本文尝试其用于重工业经济预测，力求获得一种高效的重工业领域经济预测方法。

（二）指标体系构建及数据准备

重工业是我国经济基础之一，也是第二产业的核心之一，其影响因素是多方面的。预测指标体系的构建，力求做到真实全面。由于我国地理原因、季节因素，如我国地处温带，四季气候变换较大，经济预算决策大多于二月做出，且以五年为经济计划周期，综合结合二者因素，且照顾经济连续性，采用2002-2006年五年的重工业增长数据（具体数据值见附件，数据来源国家统计局历年统计数据）进行合理分析，对于2007年度数据进行预测，为经济决策做出依据。考虑到经济系统的复杂性、多维性，根据相关分析和文献参考，建立如下预测指标体系：

表1中季度、月数及年份均是重工业影响的主要因素之一，季度由于我国位于温带，季节性气候变换对于我国重工业生产有着深刻的影响。用电量是重工业能源重要来源与投入产出量相关的重要因素。根据2002-2006年数据构造训练集，建立SVM预测模型，预测2007年重工业产量同比增加值。

（三） 预测过程

预测过程算法步骤如下：

（1）输入原始数据进行预处理，分别形成训练集样本和测试集样本；

（2）建立SVM模型，参数初始化，拉格朗日乘子 和 以及阀值b赋予随机初值；

（3）利用训练样本集建立目标函数（2），求解函数，得到拉格朗日乘子 和 以及阀值b的值；

（4）将求得的参数值带入估计函数（4）中建立预测模型，用测试样本求得下一年度的预测值；

（5）计算函数误差，当误差小于预先设定值时，结束学习过程，否则，返回继续学习

以上学习过程参见图1。

（四）预测结果及分析

表2、表3预测结果表明，对于不同参数下相同训练集，同一参数下不同训练集，算法的测试效果有所不同。从预测结果与实际数据的偏差可看出，测试集中2007年预测结果都与实际值有偏差，在0.029～0.001之间，误差范围为0.083%～3.439%。预测值总体满足以实际值为中心的正态分布要求。预测值在一月、十二月误差均较大，这与我国重工业企业绝大部分为国有企业，企业计划制定、生产过程推进带有明显计划经济的痕迹。每年一月份为我国制定本年度经济计划的时段，十二月存在为完成财政计划突击支出或收付的特殊情况，政府政策干扰较大，故预测误差较大。本文作者对于提高预测精度的建议主要有以下两点：一是利用可行的技术进行聚类分析，将远离多预测数据的预测结果舍弃，对余下的数据进行集成集中，将数据包含在平均值附近正态分布区域内；二是选择更好的核函数（目前选择的是RBF），可能会得到更加精确的预测值。

四、结论

从上述经济预测结果不难看出，样本训练数据只采用了近5年60个月度的数据，所建立SVM的经济预测模型得到的预测结果总体上还是达到了期望值的。如何选择更好的核函数和将聚类集成技术更好地应用到经济预测领域，成为未来使SVM方法在经济领域预测具有更广泛适应性的突破点。论文的研究为小样本经济预测提供一种新的有效方法。

参考文献：

[1] 杨叔子，吴雅，等. 时间序列分析的工程应用[M].北京：华中科技大学出版社， 2007.

[2] 周子英，等. 基于PCA-SVM的区域经济预测研究 [J]. 计算机仿真， 2010，4（28）：375-378.

[3] 郭崇慧，等. 宏观经济预测模型体系研究 [J]. 运筹与管理， 2001，12（4）：1-8.

[4] 周鹏，等. 一个中国宏观经济预测模型及算法 [J]. 大连理工大学学报 ，2003（3）：129-132.

[5] 彭珍端，等. 基于支持向量机的铁路客运量预测 [J]. 辽宁工程技术大学学报， 2007（26）：269-272.

[6] 张新红. 经济时间序列的连续参数小波网络预测模型 [J]. 运筹与管理，2007（4）：72-77.

[7] VAPNIK V. The Nature of Statistical Learning Theory[M]. New York：Springer Verlag，1995.

[8] 杨明. 重工业用电恢复最快，未来电力消费高企 [N].中国工业报，2010-05-06.

[9] 王信茂. 我国电力供需形势分析 [J]. 电器工业， 2004（6）：23-26.

[10] 叶小荣，等. 基于LS-SVM的经济发展水平预测 [J]. 统计与决策， 2009（17）：33-34.

（编辑：许丽丽）