基于两阶段响应面方法的结合梁斜拉桥多尺度有限元模型修正
钟儒勉 樊星辰 黄学漾 宗周红
(1东南大学土木工程学院, 南京 210096)(2福州大学土木工程学院, 福州 350108)
人类对于客观世界的认识是从不同尺度展开的,时空多尺度是客观世界的基本特征[1-2].文献[3]指出多尺度计算是在保证计算精度的同时最大限度地降低计算代价的有效途径,提出了有限元微观模型与宏观模型的界面连接方法,给出了轴向、横向和转角的约束方程,最后通过采用钢-混组合框架结构试验与数值模拟相结合的方法,对界面连接方法的有效性进行了验证.文献[4-7]指出结构的多尺度问题不是结构的刚度问题,实质上是强度问题;在进行模拟时,在不同尺度上建模,将区域分成不同尺度定律控制的区域,这些区域可以重叠也可以不重叠,并在交界处实现连接,并将多尺度建模及其模型修正应用于润扬大桥等大型桥梁健康监测之中.文献[8]从材料多尺度出发,提出了一种广义双尺度分析方法(TSA),最后通过数值试验,证明了基于有限元的TSA方法能有效反应结构的力学行为.任国武[9]从物理学的角度提出了材料多尺度模拟方法需要满足的条件,而Liu等[10]对多尺度方法进行了总结,通过引入虚拟内力法,在连接界面处可以满足力等效和能量等效,提出了一个尺度连接方法,实现计算过程的自适应.此外,Takizawa等[11]提出的基于多尺度变分方法发展了流体-结构时空多尺度方法,也可为桥梁结构的多尺度模型修正及损伤识别提供借鉴.
目前的研究侧重于结构多尺度模拟及其时空多尺度效应,多尺度模型修正大多采用与单一尺度下模型修正相同或类似的方法.单一尺度下模型修正是通过一次性的模型参数误差修正,能满足工程需求;然而,对于多尺度模型在其界面耦合的研究尚不完善的基础上,所建立的初始有限元模型往往误差过大,多尺度模型修正时将模型参数(如材料弹性模量)调整1.5~2.0倍显然是不合理的.本文将多尺度建模误差(多尺度模型与精确有限元模型之间的误差)与模型参数误差(初步修正后多尺度模型与实际结构之间的误差)区分开来且不至于失去模型修正的物理意义.以灌河大桥为工程背景,在环境振动测试的基础上,探索两阶段响应面模型修正方法的可行性和可靠性,为进一步桥梁结构多尺度损失识别及损伤预后提供较为精确的有限元模型.
1 灌河大桥环境振动试验
灌河大桥主桥采用双塔双索面半飘浮5跨连续组合梁斜拉桥,跨径组成为32.9m+115.4m+340m+115.4m+32.9m,主桥布置见图1.主梁采用工字型钢梁,钢纵梁、钢横梁、小纵梁通过节点板及高强螺栓连接形成空间钢架,钢架上架设预制桥面板,现浇膨胀混凝土湿接缝,与钢梁上的抗剪栓钉形成整体,组成组合梁体系.斜拉索采用OVM250系列环氧涂层钢绞线拉索,索塔采用空心箱形断面,C50混凝土,索塔在桥面以上高度为96.548m,2006年11月竣工通车.

图1 灌河大桥总体布置
2012年6月30日—7月1日,对灌河大桥主桥进行环境振动试验,每跨布置8个测点和1个共用参考点(见图2),每个测点布置1个三向加速度传感器,每跨作为一个测站,共7个测站;其中参考点设在跨中,测点全部布置在紧急停靠带边缘.桥面振动的采样频率为200Hz,滤波频率为200Hz,每个测站的采样时间不低于15 min.对测试所得的数据,分别基于峰值(PP)法和随机子空间(SSI)方法进行系统参数识别[12],得到灌河大桥实测的自振频率和振型.

图2 环境振动测点布置
2 多尺度有限元模型
采用大型有限元软件ANSYS进行建模分析[13],全桥共划分为2253个单元.其中斜拉索单元采用杆单元Link8;大尺度桥面系及索塔采用三主梁模型,选用beam188单元;跨中局部小尺度下,桥面板采用实体单元Soild45,主梁及小纵梁采用板壳单元Shell43;二期恒载和压重块采用mass21单元模拟.索塔底部固结,边墩、辅助墩处与梁交接处以及塔梁交接处均以弹簧单元combin14连接;通过初应变方法施加索力,并通过实测索力和线形进行结构初平衡.坐标系原点选在边墩桥面板中下部,沿桥梁纵向为Z轴,以竖向向上为+Y轴,横向为X轴,有限元模型如图3所示.将建立的多尺度模型、精细有限元模型和脊骨梁模型在同等计算条件下,比较其在模态分析时的计算效率,如表1所示.

图3 斜拉桥有限元模型

表1 模型计算效率
3 两阶段响应面模型修正
两阶段响应面模型修正[14],即将响应面方法分别应用于多尺度建模修正和模型参数修正中,其步骤为:① 将精细有限元建模计算得到的频率值作为多尺度模型的目标值,并基于三阶响应面方法对多尺度建模过程中设定的截面实常数进行修正;② 将环境振动试验得到的实测频率作为目标值,并基于三阶响应面方法对初步修正后模型的材料参数、支座参数进行修正.其基本流程如图4所示.

图4 多尺度模型两阶段响应面修正流程图
3.1 多尺度建模修正
3.1.1 精细有限元模型计算
采用大型有限元软件ANSYS进行建模分析,全桥共划分为87459个节点,46228个单元.其中斜拉索单元采用杆单元Link8;索塔和桥面板采用实体单元Soild45;主梁及小纵梁采用板壳单元Shell43;成桥状态自振特性分析时二期恒载和压重块采用mass21单元模拟.索塔底部固结,边墩、辅助墩处与梁交接处以及塔梁交接处均以弹簧单元combin14连接.坐标系原点选在混凝土梁梁端,沿桥梁纵向为Z轴,以竖向向上为+Y轴,横向为X轴,最终的有限元模型如图5所示.

图5 斜拉桥精细有限元模型
3.1.2 修正参数筛选
在多尺度建模过程中,宏观尺度下梁单元实常数的选取往往是通过初步近似计算得到的,特别是结合梁斜拉桥,其各部分的协同工作程度对于截面实常数的影响较大,难以估量的实常数选取造成了建模过程中的误差,本文根据工程竣工图和经验给出待修正参数(筛选)如表2所示.
3.1.3 三阶响应面模型修正
在多尺度建模修正中,采取三阶响应面方法对选择的参数进行修正.其步骤如下:① 基于D最优设计方法,选择30组设计样本,并将样本参数代入多尺度有限元模型中,计算得到竖向前3阶频率,如表3所示.② 选取三阶响应面函数,应用最小二乘法回归分析技术对样本数据进行拟合,即

表2 多尺度模型待修正参数(筛选)

表3 试验样本值

(1)
式中,R1为竖向一阶振动频率.式(1)为竖向基频的响应面拟合函数.响应面模型与各参数关系如图6所示.
对回归后的响应面模型进行精度检验以保证其可靠性,计算参数范围内的相关系数R2及均方根误差RMSE值,即
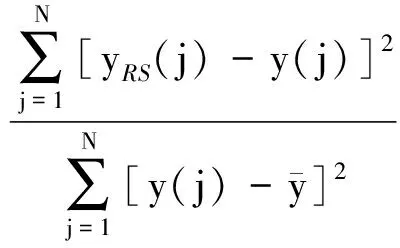
(2)

(3)

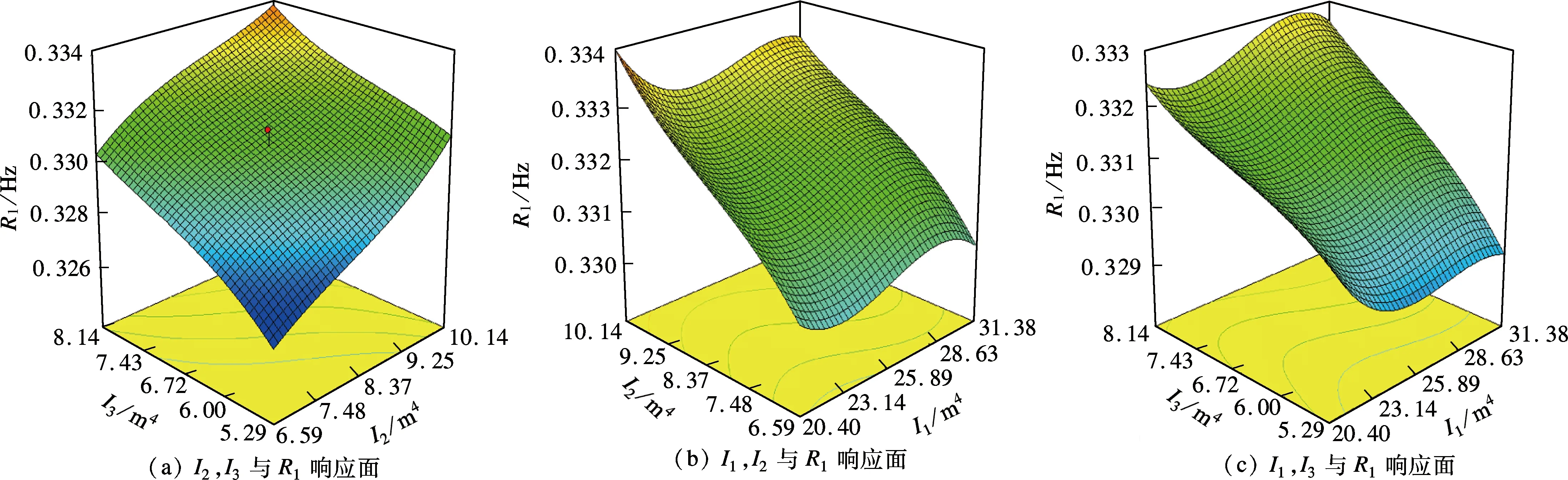
图6 竖向一阶频率响应面

表4 竖向振动响应面模型精度检验值
如表5所示,将修正后的参数代入有限元模型进行计算,并将计算得到的频率与实测结果进行比较,结果如表6所示.从表中可以看出,响应面模型修正后计算得到的频率与精细模型计算得到的频率吻合较好,最大误差不超过10%,说明能采用初步修正后的多尺度模型对实桥进行有限元模型计算.

表5 修正后参数值与初始值比较 m4

表6 修正后频率与实测频率比较
3.2 模型参数修正
3.2.1 修正参数筛选
在模型参数修正中,根据灌河大桥桥梁检测报告,选取材料弹性模量、支座弹簧刚度等作为修正参数[14],并且根据工程经验和强度等级分布等给出待修正参数,即桥面板混凝土弹性模量E1、各支座纵向弹簧刚度K1、桥塔处支座横向弹簧刚度K2、边墩及辅助墩处横向弹簧刚度K3.
3.2.2 三阶响应面模型修正
在模型参数修正中,采取三阶响应面方法对选择的参数进行修正.其步骤同上,表7为试验设计的样本点,竖向基频的响应面拟合函数为
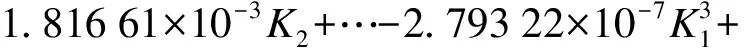
(4)
图7为各参数与竖向、横向、纵向一阶频率的关系图.对回归后的响应面模型进行精度检验以保证其可靠性,分别运用式(2)、(3)计算参数范围内的R2及RMSE值,结果见表8.由表可见,R2值很接近1,RMSE值很接近0,说明响应面函数计算值与真值之间的差异程度很小.因此,在参数设计空间内,响应面函数能有效地反映结构响应和参数之间的关系,回归的响应面模型可以替代有限元模型用于模型修正.

表7 试验样本值

图7 各参数与竖向、横向、纵向一阶频率的关系图

表8 各阶振动响应面模型精度检验值
由表9可以看出,修正后的参数仍然具有其真实的物理意义.再将修正后的参数代入多尺度模型进行计算,并将计算得到的结果与精细模型结果进行比较,如图8和表10所示.由此可见,面模型修正后计算得到的频率与实测频率吻合较好,最大误差不超过8%.
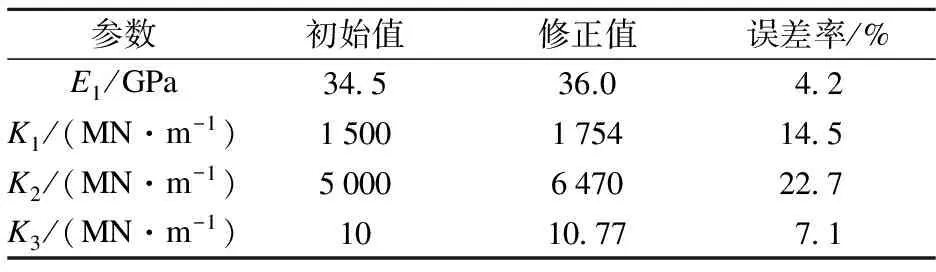
表9 修正前后参数值比较

图8 灌河大桥实测与计算振型比较
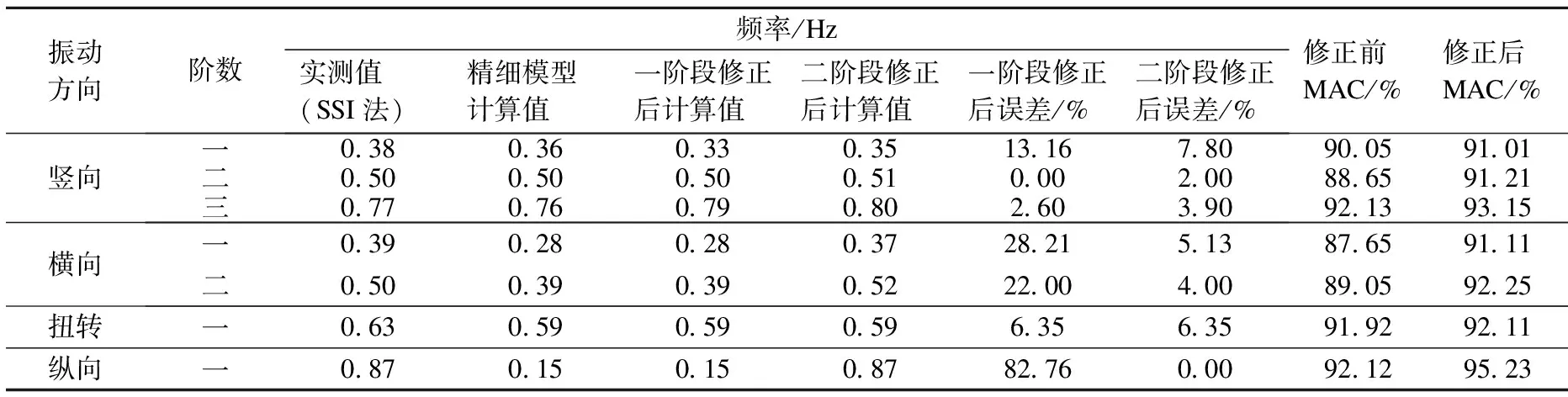
表10 修正后的频率与实测频率的比较
4 结论
1) 基于环境振动试验和响应面方法,建立了基于两阶段响应面的斜拉桥结构多尺度模型修正方法.灌河大桥多尺度有限元模型表明:基于两阶段响应面方法修正后的计算频率与实测频率吻合较好,最大相对误差不超过8%,MAC值基本在90%以上,说明两阶段响应面方法能够较好地进行多尺度模型修正,且修正后的模型参数仍然具有其物理意义而不失真.
2) 探讨了基于不同来源的模型误差修正方法,在多尺度模型修正中,可将多尺度建模误差与模型参数误差区分开来进行修正,为多尺度模型修正提供了一种思路.修正后的有限元模型可以进一步应用于多尺度有限元模型确认、多尺度损伤识别及损伤预后,服务于桥梁健康监测和安全评估.
)
[1] James G, Sharp D. Multi-scale science: a challenge for the twenty-first century [J].AdvancesinMechanics, 1998,28(4): 545-551.
[2] Bazant Z P, Chen E P. Scaling of structural failure [J].ApplMechRev, 1997,50(10): 593-627.
[3] 林旭川,陆新征,叶列平. 钢-混凝土混合框架结构多尺度分析及其建模方法[J].计算力学学报,2010, 6(3): 469-475.
Lin Xuchuan, Lu Xinzheng, Ye Lieping. Multi-scale finite element modeling and its application in the analysis of a steel-concrete hybrid frame [J].ChineseJournalofComputationalMechanics, 2010,6(3):469-475. (in Chinese)
[4] Li Z X, Zhou T, Tommy H T, et al. Multi-scale numerical analysis on dynamic response and local damage in long-span bridges[J].EngineeringStructures, 2007,29(7): 1507-1524.
[5] 孙正华,李兆霞,陈鸿天. 大跨斜拉桥结构行为一致多尺度有限元模拟[J].中国公路学报,2009,9(5): 68-74.
Sun Zhenghua, Li Zhaoxia, Chen Hongtian. Concurrent multi-scale finite element modeling of long-span cable-stayed bridge [J].ChinaJournalofHighwayandTransport, 2009,9(5):68-74. (in Chinese)
[6] 李兆霞,王滢,吴佰建, 等 桥梁结构劣化与损伤过程的多尺度分析方法及其应用[J].固体力学学报,2010,31(6): 731-756.
Li Zhaoxia, Wang Ying, Wu Baijian, et al. Muti-scale modeling and analysis on structural deterioration and damage in long-span bridges and its application[J].ChineseJournalofSolidMechanics, 2010,31(6):731-756. (in Chinese)
[7] Li Z X, Jiang F F, Tang Y Q. Multi-scale analyses on seismic damage and progressive failure of steel structures[J].FiniteElementsinAnalysisandDesign, 2012,48(2): 1358-1369.
[8] Cui J Z, Shi T M, Wang Y L. The two-scale analysis method for bodies with small periodic configurations [J].StructuralEngineeringandMechanics, 1999,7(6): 601-614.
[9] 任国武. 材料的多尺度模拟[D].上海:复旦大学物理学院,2010.
[10] Liu Wing Kam, Qian Dong, Gonella Stefano, et al. Multiscale methods for mechanical science of complex material: bridging from quantum to stochastic multi-resolution continuum [J].InternationalJournalforNumericalMethodsinEngineering, 2010,83(8/9):1039-1080.
[11] Takizawa K, Tezduyar T E. Multiscale space-time fluid-structure interaction techniques [J].ComputationalMechanics, 2011,48(3):247-267.
[12] Ren Weixin, Zong Zhouhong. Output-only modal parameter identification of civil engineering structures [J].InternationalJournalofStructuralEngineeringandMechanics, 2004,17(3/4):429-444.
[13] 郝文化. ANSYS在土木工程应用实例[M].北京:中国水利水电出版社,2005.
[14] 宗周红,任伟新. 桥梁有限元模型修正与模型确认[M].北京:人民交通出版社,2012:109-117

