基于实测与规范风谱的三塔悬索桥抖振性能对比

王 浩 陶天友 郭 彤 李爱群 邓稳平

(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)

随着跨径的增加,悬索桥结构变得极为细柔,在风荷载作用下的响应逐渐占据主导作用[1-4]．泰州长江公路大桥(以下简称泰州大桥)为主跨2×1080m的三塔双跨钢箱梁悬索桥,系世界首创．与两塔悬索桥相比,中塔的引入使得三塔悬索桥的受力特点与动力特性变得更加复杂,在风荷载激励下的响应应该给予密切关注．抖振作为桥梁风致振动最突出的形式之一,已成为桥梁抗风研究中的重点课题之一,且已开展了大量相关研究[5-7],然而,国内外对于三塔悬索桥抗风性能的研究很少．鉴于大跨度三塔悬索桥新颖的结构型式及其复杂的受力特点,开展其抖振研究具有重要的理论意义与工程应用价值．

我国地处亚洲大陆东部,地域广大,不同的地形特点会引起所在地风场特性的差异,因而单一的抗风规范很难完整地诠释全国各地的风谱模型[8]．本文以世界第一大跨度三塔悬索桥——泰州大桥为工程背景,采用实测风谱对该桥设计阶段基于规范谱所进行的抖振分析进行对比验证．实测风谱源自本课题组多年来在润扬长江大桥桥址区、苏通长江大桥桥址区的多次台风现场实测以及结构健康监测系统[9]数据库所获得的海鸥、凤凰、卡努、麦莎、冬季强北风等数据资料．根据以上实测资料,采用非线性最小二乘法对桥址区实测强风紊流功率谱密度函数进行拟合,获得实测风谱曲线,并分别以实测风谱和规范谱为目标谱模拟桥址区的三维脉动风场,基于ANSYS对泰州大桥进行非线性时域抖振响应的对比分析,结果可为三塔悬索桥抖振分析及抗风设计提供参考．

1 工程背景

泰州大桥位于江苏省境内长江中段,桥位处江面宽约2.4km,河床呈“W”形,综合考虑桥位处河势水文与航道状况以及深水岸线的充分利用,设计时主桥桥跨结构布置为390m+1080m+1080m+390m的两主跨三塔悬索桥(见图1)．加劲梁采用封闭式流线型扁平钢箱梁,加劲梁设上斜腹板及下斜腹板构成导风嘴．钢箱梁节段标准长度为16m,中心线处梁高3.5m．主缆在设计成桥状态矢跨比为1/9,2根主缆横向间距为35.8m．索塔采用门式框架结构,两边塔为混凝土塔,中间塔为钢塔,边塔高178.0m,中塔高182.5m．2个边塔在顺桥向为单柱形结构,而中间桥塔在顺桥向则采用倒Y形结构,以增强纵向刚度．

图1 泰州大桥结构布置图(单位:m)

该三塔悬索桥边跨无悬吊加劲梁,中塔下横梁上不设竖向支座,也不设0号索,在中塔横梁与主梁间设横向抗风支座,限制主梁的横向位移,竖向采用限位挡块．中塔处设弹性索适当限制纵向位移;下塔柱底部与沉井上盖板相连;边塔处设置竖向拉压支座、侧向抗风支座和纵向阻尼支座．

2 结构有限元模型

基于大型有限元分析软件ANSYS平台建立了泰州大桥的有限元计算模型,如图2所示．在该有限元模型中,加劲梁采用鱼骨梁式的计算模型,加劲梁和桥塔等构件简化为空间梁单元,加劲梁按吊杆的吊点进行离散．主缆、吊杆则简化为空间杆单元,主缆按吊杆的吊点进行离散,其弹性模量采用Ernst等效弹模公式进行计算[10]．主梁与吊杆之间采用刚性横梁模拟,横梁采用刚臂(刚度极大的无质量梁单元)模拟．分析中将主梁的质量平均分配到各节点上,通过节点上的集中质量惯矩来考虑主梁分布质量惯矩的作用．根据结构设计图纸,耦合了主梁与边塔在竖向、横桥向以及绕顺桥向的转动自由度,同时耦合了主梁与中塔在横桥向的自由度．在边、中塔下横梁与加劲梁交界处设置Combin14非线性阻尼器单元,以模拟用于控制纵桥向位移的弹性拉索和纵向阻尼支座,并将同一位置设置同向阻尼器,通过改变阻尼系数来等效多个阻尼器在该方向上的输出力．主缆和主塔底部完全固结,未考虑土-桩-结构相互作用．

图2 泰州大桥空间有限元计算模型

3 泰州大桥三维脉动风场的模拟

分别以《公路桥梁抗风设计规范》[11]中的规范谱和实测风谱为目标谱,结合大跨度三塔悬索桥的结构特点对基于谱特性的三维脉动风场进行了简化模拟,并从功率谱和相关性2个方面验证了该模拟方法,旨在为该桥抖振响应非线性时域分析提供准确可靠的脉动风速时程．

泰州大桥风场可以简化成5个独立的一维多变量随机风场,如表1所示．运用风场模拟的谐波合成法,对沿跨度方向80m(钢箱梁标准节段长度的5倍)等间距分布的主梁风场和沿竖向30m等间距分布的主塔风场进行了模拟．模拟点分布如图3所示．

表1 简化的5个独立一维脉动风场

3.1 实测风谱模型

2005年—2012年间,本课题组在润扬大桥、苏通大桥进行多次台风实测并基于桥梁结构健康监测系统数据库得到了海鸥、凤凰、韦帕、卡努、麦莎、冬季強北风等数据资料．基于Matlab平台,经过数据预处理进行了桥址区风特性分析,运用FFT技术得到实测风谱的PSD(power spectrum density)函数．运用非线性最小二乘法对纵向及竖向的经验谱进行拟合以得出实测风谱(见图4)．

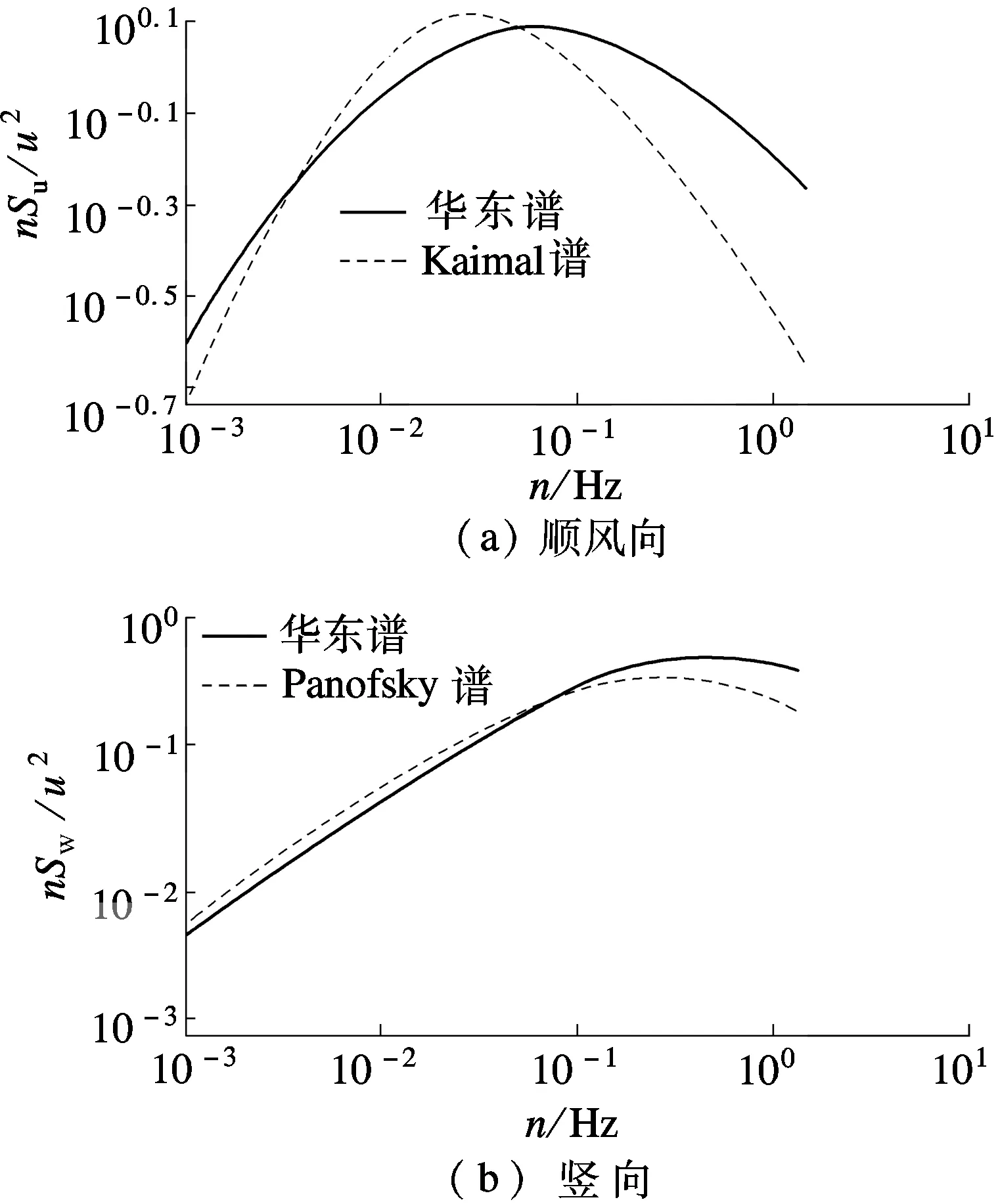
图4 实测风谱与规范风谱对比图

高度Z处平均风速U(z)的顺风向脉动风功率谱密度函数为

(1)

竖向脉动风功率谱密度函数为

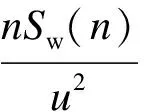
(2)

式中,Su(n)为顺风向功率谱密度函数;Sw(n)为竖向功率谱密度函数;n为自然风的脉动频率;f为莫宁坐标;u为气流摩阻速度．

3.2 主梁风场模拟

运用谐波合成法[12]获得该桥主梁28个点的横桥向与竖向脉动风速时程,主梁横桥向目标谱分别采用Kaimal谱[13]和实测谱的顺风向谱,竖向采用Panofsky谱[14]和实测谱的竖向谱,脉动风速谱的相干函数采用Davenport相干函数[1]．选用其他参数具体如下:截止频率ωu=4π rad/s;频率分段数N=1024;样本时距Δt=0.25s;选用时段长1800s．根据现行《公路桥梁抗风设计规范》,取桥址区百年一遇设计风速为模拟风速,即6.6m高度处平均风速为27.1m/s,根据风速沿高度的指数变化规律对主梁和主塔高度处风速进行换算．共计生成了50个风场样本,并从功率谱和相关性2个方面对模拟结果进行了校核．图5给出了主梁模拟自谱与目标谱的对比图,图6给出了主梁模拟风场相关函数与理论值的对比图．

由上述功率谱和相关函数对比图可知,模拟谱与目标谱对应值十分接近,模拟的相关函数与理论值也相差不大,验证了本文所采用的三维脉动风场模拟方法的准确性与可靠性．

3.3 主塔风场模拟

由于桥塔上各点的风速不同,模拟桥塔的风速时程时,互谱密度函数需要考虑相位角．风谱密度矩阵(复数矩阵)有可能不正定,根据对应风谱密度矩阵题正定性将风频值划分为正定和不正定区间．在风频值正定区间内,可直接将风谱密度矩阵进行Cholesky分解;而在风频值不正定区间内,采用插值技术近似获得风谱密度矩阵分解式[15]．

主塔顺风向目标谱分别采用Kaimal谱[13]和实测谱的顺风向谱，脉动风速谱采用Davenport相干函数[1]．选用其他参数如下:截止频率ωu=4π rad/s;频率分段数N=1024;样本时距Δt=0.25s;选用时段长1800s．同样利用上述参数生成了50个风场样本,并对模拟结果进行了校核．图7和图8分别给出了主塔模拟脉动风速在功率谱与相关性2个方面的对比,对比分析说明谐波合成法的正确性,可为后续大桥风致抖振时域分析奠定基础．

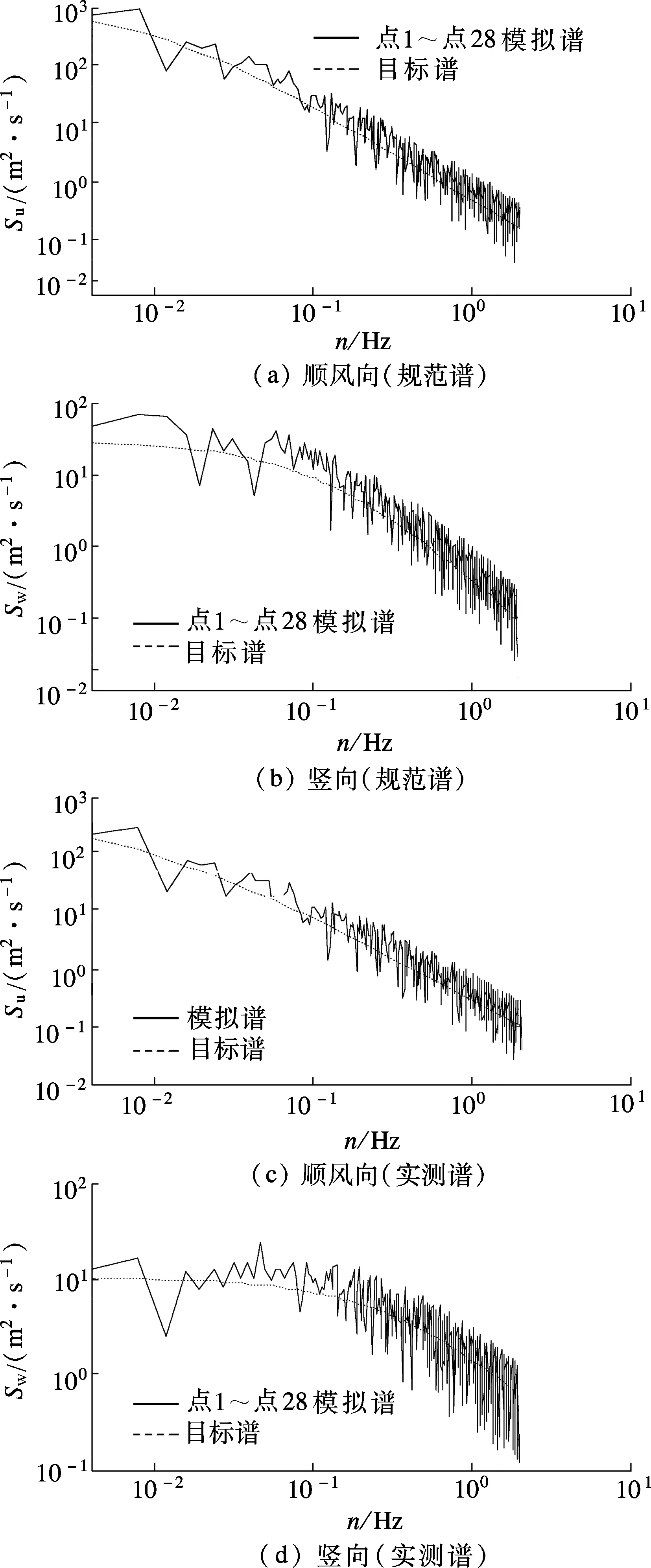
图5 主梁模拟自谱与目标谱对比

4 泰州大桥抖振响应分析

4.1 基于ANSYS的三塔悬索桥抖振时域分析方法

在上述风场模拟的基础上,基于ANSYS的瞬态动力学分析功能,进行了该桥抖振响应的非线性时域分析,其中计入了气动自激力的影响,具体包括如下步骤:① 基于参数化设计语言APDL建立了大桥有限元计算模型;② 为了便于APDL进行调用,将主梁断面的静力三分力系数、颤振导数等以Table方式存储;③ 根据模拟风场中的风速数据和颤振导数值确定用于模拟气动刚度和气动阻尼的Matrix27单元的参数[16],得到了便于抖振分析、考虑气动自激力影响的有限元模型;④ 采用风洞实测静力三分力系数计算静风荷载;⑤ 根据Devaport经典公式计算抖振力时程;⑥ 将风荷载施加到结构有限元模型上,并进行瞬态动力学求解,分析过程中考虑几何非线性的影响;⑦ 进入后处理查看结构的时程响应分析结果,求出统计量(如位移响应RMS值等)．

图6 主梁相关函数对比(点1～点28)

4.2 泰州大桥抖振位移响应RMS分布

采用上述抖振时域分析方法进行分析,计算时长取30min,时间步长取0.25s,共计7200个荷载子步．根据输入的规范谱及实测谱模拟风场,得到泰州大桥沿跨度方向的抖振位移响应RMS值分布,如图9所示．

图7 中塔模拟自谱与目标谱对比

图8 中塔相关函数对比(点29～点35)

图9表明:① 泰州大桥各主跨主梁沿跨度方向侧向抖振位移RMS值(LRMS)分布与两塔悬索桥类似,均表现为由跨中向两侧递减,在边塔或中塔处为0,此现象归结于主梁在中塔与边塔处横向设抗风支座,限制主梁侧向位移．② 主梁沿跨度方向竖向与扭转抖振位移RMS值(VRMS和TRMS)的分布表现出泰州大桥独有特点，主梁扭转抖振位移RMS值分布表现为由跨中向两侧递减,在边塔处为0,中塔处大于0;主梁竖向抖振位移RMS值分布呈现多极值,其中边塔处RMS值为0,RMS值最大出现在跨中附近,极小值出现在距中塔约200m处,中塔处为另一极值点．主梁于边塔处竖向设拉压支座,于中塔下横梁处设竖向限位挡块且未设0号索，这是形成三塔悬索桥竖向与扭转抖振位移RMS值变异性的主要原因．③ 基于实测谱的抖振位移RMS值均小于规范谱,表明基于规范谱的抖振计算结果偏于保守,采用实测谱使得泰州大桥抖振计算更加精细化．

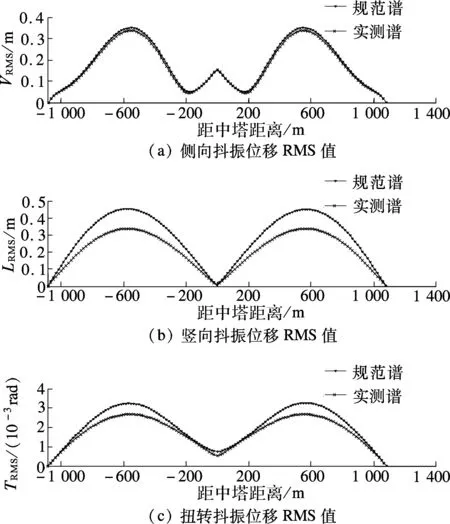
图9 主梁沿跨度方向抖振位移响应RMS值分布图

4.3 泰州大桥主梁抖振位移响应功率谱对比分析

为了分析大桥各阶振型对抖振响应的贡献,进行了抖振位移响应的功率谱分析．由于主梁所受约束由跨中向边塔逐渐减小,跨中的风致抖振响应往往最大,因此选择跨中位置为代表进行泰州大桥抖振位移响应功率谱分析．基于FFT技术将跨中抖振响应时程由时域转换到频域,进行不同风谱下主梁跨中抖振位移响应功率谱比较(见图10)．为了统一单位,图中扭转位移已乘以主梁宽度的1/2．

不同风谱下主梁跨中位移功率谱密度表明:① 采用实测谱与规范谱的主梁跨中抖振位移功率谱密度曲线的整体趋势及峰值出现位置基本一致,其中低频区表现不一,高频区基本相同．② 泰州大桥竖向抖振位移响应功率谱密度曲线的第一个峰值对应结构自振特性的第二阶振型,为主梁第一阶反对称竖弯振型;侧向位移响应功率谱密度曲线的第一个峰值对应结构自振特性的第一阶振型,为主梁第一阶反对称侧弯振型;扭转位移响应功率谱密度曲线的第一个峰值对应结构自振特性的第十三阶振型,为主梁第一阶反对称扭转振型．可见,各方面的第一阶振型对泰州大桥主梁抖振响应贡献最大．

5 结论

1) 采用实测谱与规范谱的主梁跨中抖振位移功率谱密度曲线的整体趋势及峰值出现位置基本一致,其中低频区表现不一,高频区基本相同.

2) 泰州大桥主梁的竖向抖振响应主要由结构第一阶反对称竖弯振型控制,侧向抖振响应主要由结构第一阶反对称侧弯振型控制,扭转抖振响应主要由结构第一阶反对称扭转振型控制．各方向的第一阶振型对泰州大桥主梁抖振响应贡献最大．

3) 泰州大桥各主跨主梁沿跨度方向侧向抖振位移RMS值分布与两塔悬索桥类似,均表现为由跨中向两侧递减,在边塔或中塔处为0,这主要是由于泰州大桥主梁在边塔和中塔处设横向抗风支座,限制主梁侧向位移．

4) 在靠近中塔附近,主梁沿跨度方向竖向与扭转抖振位移RMS值分布表现出泰州大桥的独有特点:主梁扭转抖振位移RMS值在中塔处大于0,主梁竖向抖振位移RMS值分布呈现多极值．这主要是由于主梁在边塔位置设竖向拉压支座,在中塔下横梁处设竖向限位挡块且未设0号索．

5) 就本次研究而言,采用规范谱的抖振位移响应RMS值与采用实测谱相比偏于保守,因此从数值计算的结果来看:采用基于实测的实测谱更有利于进行大跨度桥梁抖振精细化研究,而规范谱的计算偏于安全,可用于工程设计．

必须指出,本文的实测风谱模型仅由苏通和润扬2座大桥处的实测风速资料得到,且由于两桥结构健康监测系统运营时间尚短,使得实测风速资料有限,这也是文章的不足之处．随着未来南京长江四桥、泰州大桥等大跨度桥梁的相继建成,以及监测数据随时间的不断积累,本文所提出的实测风谱模型也将进一步完善,这也是作者未来的研究方向．

)

[1] Simiu E, Scanlan R H.Windeffectsonstructures[M]. New York: John Wiley & Sons, INC, 1996.

[2] Scanlan R H. The action of flexible bridge under wind. Part 2: buffeting theory[J].JournalofSoundandVibration, 1978,160(2): 201-211.

[3] 项海帆, 葛耀君, 朱乐东, 等. 现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005.

[4] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005.

[5] 李永乐, 廖海黎, 强士中. 三塔斜拉桥抖振的耦合行为研究[J]. 工程力学, 2004, 21(4): 184-188.

Li Yongle, Liao Haili, Qiang Shizhong. Coupled behavior in buffeting response of three-pylon cable-stayed bridge[J].EngineeringMechanics, 2004,21(4): 184-188.(in Chinese)

[6] 闵志华, 孙利民, 淡丹辉. 台风下斜拉桥风致振动和动力特性分析[J]. 同济大学学报:自然科学版, 2009, 37(9): 1139-1145.

Min Zhihua, Sun Limin, Dan Danhui. Analysis of wind-induced response and dynamic properties of cable-stayed bridge under typhoon[J].JournalofTongjiUniversity:NaturalScience, 2009,37(9): 1139-1145.(in Chinese)

[7] 郭薇薇, 夏禾, 徐幼麟. 风荷载作用下大跨度悬索桥的动力响应及列车运行安全分析[J]. 工程力学, 2006, 23(2): 103-110.

Guo Weiwei, Xia He, Xu Youlin. Dynamic response of long span suspension bridge and running safety of train under wind action[J].EngineeringMechanics, 2006,23(2): 103-110.(in Chinese)

[8] 王浩, 李爱群, 焦长科, 等. 基于规范及实测风谱的苏通大桥抖振响应对比研究[J]. 土木工程学报, 2011, 44(10): 91-97.

Wang Hao, Li Aiqun, Jiao Changke, et al. Comparable study of the buffeting response of Sutong Bridge based on specification and measured wind power spectrum[J].ChinaCivilEngineeringJournal, 2011,44(10): 91-97.(in Chinese)

[9] 李惠, 周文松, 欧进萍,等. 大型桥梁结构智能健康监测系统集成技术研究[J]. 土木工程学报, 2006, 39(2): 46-52.

Li Hui, Zhou Wensong, Ou Jinping, et al. A study on system integration technique of intelligent monitoring systems for soundness of long-span bridges[J].ChinaCivilEngineeringJournal, 2006,39(2): 46-52.(in Chinese)

[10] Ernst H J. Der e-modul von seilenunterber?cksichtigung des durchhanges[J].DerBauingenieur, 1965,40(2): 52-55. (in German)

[11] 中交公路规划设计院.JTG/TD 60-01—2004公路桥梁抗风设计规范[S].北京：人民交通出版社，2004.

[12] Shinozuka M, Jan C M. Digital simulation of random processes and its application[J].JournalofSoundandVibration, 1972,25(1): 111-128.

[13] Kaimal J C. Spectral characteristics of surface layer turbulence[J].JournaloftheRoyalMetaorologicalSociety, 1972,98(1): 563-589.

[14] Panofsky H A, McCormick R A. The spectrum of vertical velocity near the surface[J].JournaloftheRoyalMetaorologicalSociety, 1960,86(370): 546-564.

[15] 贺艺华, 蒋友宝, 张建仁. 考虑相位角的脉动风场模拟[J]. 工程力学, 2008, 25(12): 25-29.

He Yihua, Jiang Youbao, Zhang Jianren. Simulation of turbulent wind field with phase angle[J].EngineeringMechanics, 2008,25(12): 25-29.(in Chinese)

[16] 华旭刚, 陈政清, 祝志文. 在ANSYS中实现颤振时程分析的方法[J]. 中国公路学报, 2002, 15(4): 32-34.

Hua Xugang, Chen Zhengqing, Zhu Zhiwen. Approach of time-history analysis of flutter in ANSYS[J].ChinaJournalofHighwayandTransport, 2002,15(4): 32-34.(in Chinese)