星载SAR在轨成像实时处理算法研究

边明明 李盛林 岳荣刚

（中国空间技术研究院，北京 100094）

1 引言

随着星载合成孔径雷达（SAR）技术和应用的不断发展，在星上完成SAR 成像处理具有重要意义，通过在轨实时成像处理形成图像，再将光学形式的遥感图像在图像域进行数据处理后传输到地面。由于星载SAR 在轨处理改变了传统的卫星数据通过数据传输链路到地面接收处理的模式，星载SAR 在轨成像处理的工程实现还存在一系列需要研究的问题，例如代价问题、工程实现问题、传输效率问题、图像质量问题等，其中代价问题需要考虑SAR 数据星上处理相比于地面处理所带来的卫星系统问题，比如系统的复杂度、功耗、可靠性等；工程实现问题需要综合考虑SAR 在轨成像处理的全过程，包括星上原始数据实时成像处理、SAR 图像压缩、数据传输链路、地面接收应用等问题；图像质量问题需要研究SAR 成像在轨处理的辐射校正、几何校正以及卫星姿态稳定度对图像质量的影响等等。

因此，星载SAR 在轨成像处理是一个较复杂的问题，需要进行系统的考虑，本文仅从星上原始数据实时成像处理以提高成像效率这一点入手，对星载SAR 在轨处理进行初步的探索研究。

2 星载SAR 成像处理的实时性约束

随着卫星分辨率、幅宽等指标的不断提高，形成的原始数据量大，给数传通道带来了压力，为了降低数传通道的传输压力，可以考虑在图像域进行大压缩比处理降低数据率的方式进行传输，鉴于此星载SAR 在轨成像处理系统对遥感数据处理算法的实时性提出了严格的要求，具体对算法的约束可分为以下两个方面：

1）星上处理系统能力对算法的约束

在地面遥感数据处理中可以通过系统扩展，增强软硬件处理能力以达到实时处理，所以在地面应用中对算法的实时性要求并不是很严格，而星上处理系统受体积、重量、功耗等强约束的限制，处理系统不能无限制的扩展，这就要求对算法进行实时性改进和优化，从算法源头上提高星上SAR处理的实时性。

2）星上处理系统输入数据对算法的约束

星上处理系统获取的是未经任何处理的原始数据，不仅数据量大，而且数据率高，这样对星上SAR处理系统的实时处理能力、存储能力、吞吐能力都提出了很高的要求。因此，要实现星载SAR 在轨实时成像处理，首先需要针对星上实时获取的数据特点，开展星载SAR 处理算法的实时性研究，使算法适用于高分辨率、大入射角、宽测绘带等条件下的星载SAR 在轨实时成像处理系统。

3 星载SAR 成像算法与运算量比较

SAR 回波信号是由天线波束照射区内目标的后向散射系数通过一个二维线性系统所构成的，SAR 成像处理的实质就是从回波中提取后向散射特性的过程，在处理过程中，各种SAR 成像算法的区别在于如何定义雷达与目标的距离模型，以及如何解决距离-方位耦合问题，这个问题直接导致了各种算法在成像质量和运算量方面的差异。比较经典的高精度SAR 成像处理算法有波束域（ω-k）算法、CS（Chirp Scaling）算法和距离多普勒（RD）算法，如图1所示［1-7］。

RD 算法是一种经典的SAR 成像算法，在距离徙动不大的情况下，是一种优秀的SAR 成像算法，但是随着距离徙动的增加，计算量会急剧增大，另外RD 算法需要插值运算，这在增加计算量的同时，还会引入误差，而改进的CS 和波束域两种算法成像性能接近，均能对大距离徙动条件下星载SAR 进行精确成像，图像质量均能满足指标要求，现针对CS和波束域算法的运算量进行分析比较。

设SAR 成像过程中，距离向点数为N，方位向点数为M。经计算，CS 算法所需的总计算量为18NM＋10NM［lb（NM）］次浮点运算，而波束域算法的总计算量为70NM＋10NM［lb（NM）］＋5M·lbM，以16K×16K（距离×方位）点目标数据为例，波束域算法的计算量大约是改进的CS算法的1．2倍，另外波束域算法需要stolt插值，增加了算法实现的复杂性，而改进CS算法结构简单，只需要傅里叶变换（FFT）、逆傅里叶变换（IFFT）和复数乘法就能够完成成像过程。本文以CS 算法为例，仅从实时处理角度对其进行改进研究，以进一步减少运算量、提高处理速度。

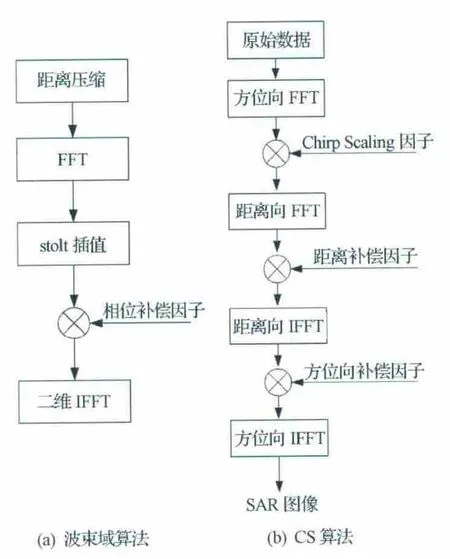
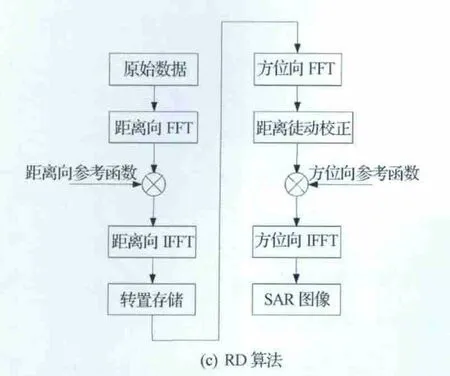
图1 经典的高精度SAR 成像处理算法Fig．1 Classic high precision SAR imaging processing algorithm

4 补偿因子对成像实时性的影响

在如图1所示的CS算法流程中一共有三个阶段需要用到补偿因子进行相位补偿，它们分别是方位向FFT 处理后的Chirp Scaling 因子、距离向FFT 后的距离补偿因子和方位向处理阶段的方位补偿因子，每个阶段在进行相位补偿时，补偿因子都要随着距离门变化而不断更新，而补偿因子的计算过程又相对复杂，因为补偿因子的计算含有乘加以外的超越运算，主要包括三角函数、开方运算，这些运算在硬件实现的过程中会比较困难，其计算量占整个CS算法的比例为

当M＝N＝1024时，补偿因子计算量大约占总运算量的8．2%，更为重要的是，补偿因子的计算会使成像处理硬件系统的处理、存储、吞吐难以达到平衡，使得硬件的处理能力难以得到最佳发挥，整个处理系统的效率得不到提升，严重影响了SAR 成像处理的实时性。

5 补偿因子区域不变的CS算法

5．1 算法描述

由CS算法可以知道，Chirp Scaling因子φ1（τ，f，Rref）、距离补偿因子φ2（fτ，f）、方位补偿因 子φ3（τ，f）理论上都是随距离门变化的，其中τ为距离向时间域，f为方位向频域，fτ为距离向频域，Rref为参考距离。然而，如果补偿因子在一定的距离门内不发生变化，由此所带来的成像质量的损失又在系统可接受的范围之内，那么补偿因子的计算量将会成倍地降低，从而有效提高星上SAR 成像处理的实时性。基于这种思想，本文提出一种补偿因子区域不变的CS算法，其计算流程如图2所示。

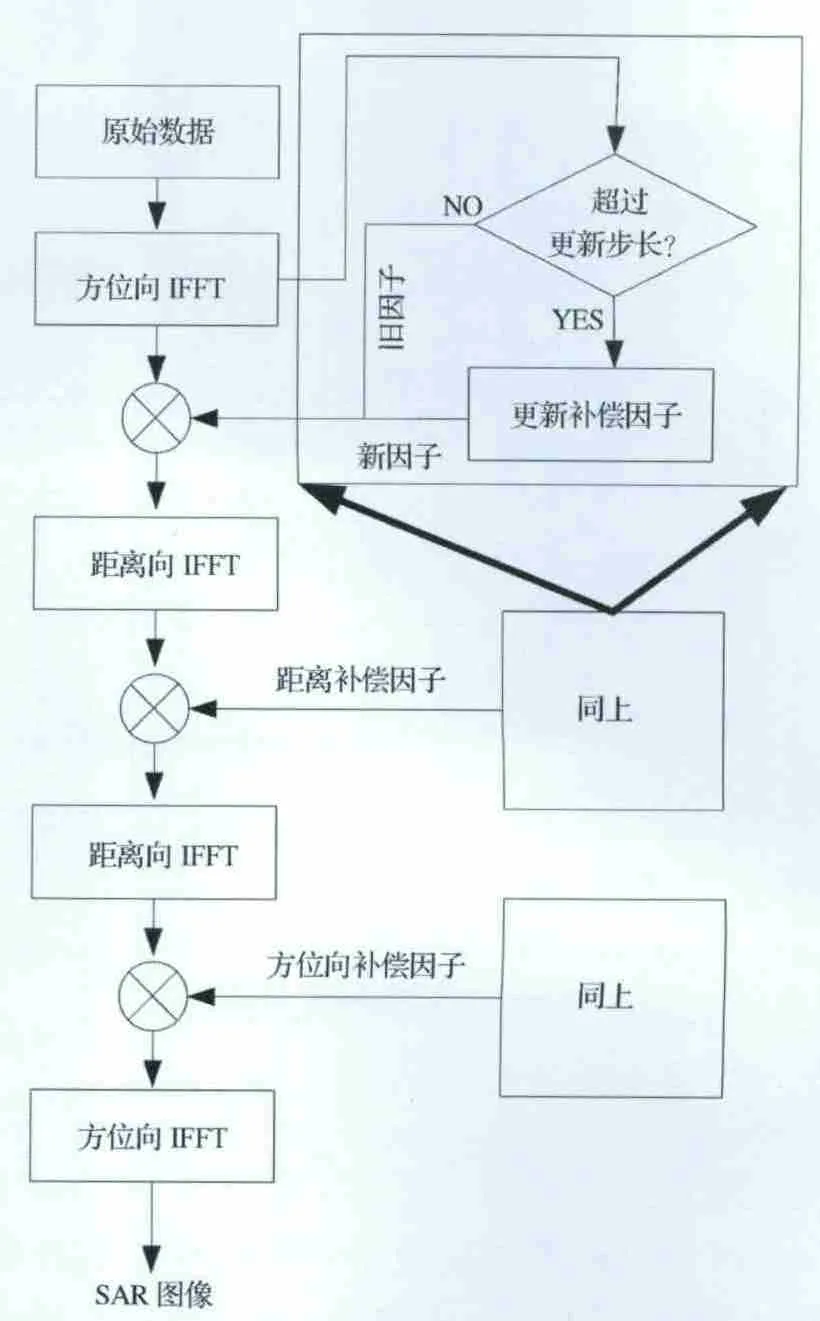
图2 补偿因子区域不变的CS算法流程Fig．2 Flow chart of constant-in-region of PCF CS algorithm

和经典的CS 算法一样，补偿因子区域不变的CS算法也经过了三个阶段的相位补偿，最后在距离多普勒域通过方位向IFFT 得到SAR 图像，只是在更新补偿因子时需要判断当前的补偿因子是否超过了更新步长，如果超过了更新步长，则需要对补偿因子进行计算更新，将新得到的补偿因子去补偿相位，如果没有超过更新步长，则在进行相位补偿时仍采用上一次更新的补偿因子。因此，如何确定更新步长则成为一个关键问题。

5．2 更新步长的确定

更新步长上限的确定，可以分为更新步长粗略估计和更新步长精确确定两个步骤，如图3所示，其中更新步长的粗略估计可以通过推导相位补偿误差与更新步长的变化关系式并观察其变化曲线来完成；更新步长的精确确定可以通过实验法对点目标和点阵进行成像仿真，然后对成像结果进行指标评估来完成。

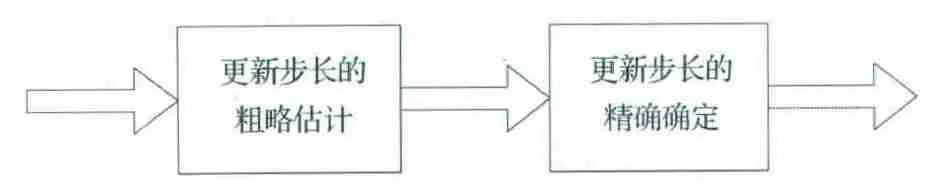
图3 更新步长上限的确定步骤示意图Fig．3 Choice approach of updating step（upper limit）

1）更新步长上限的粗略估计在图2所示的补偿因子区域不变CS算法流程中，由于补偿因子没有严格地随着距离门变化而变化，所以，在进行相位补偿时必然存在补偿误差，参考文献［8-10］的公式推导，设更新步长为ΔR，那么在CS算法的三个步骤中，相位补偿误差为

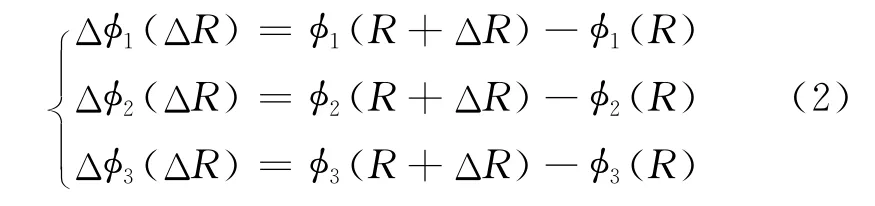
针对表1所示的卫星实验参数，Δφ1、Δφ2、Δφ3与ΔR的关系曲线如图4所示。

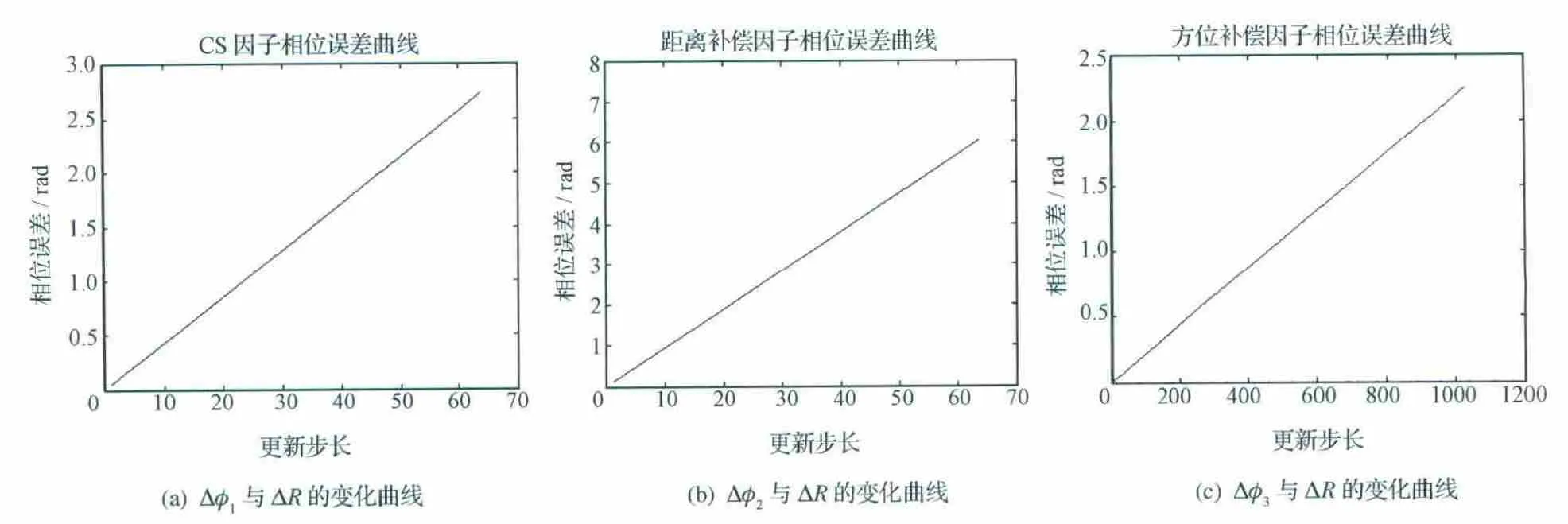
图4 相位补偿误差与ΔR 的变化曲线Fig．4 Compensation error with updating step

从图4 可以看出，在CS 算法流程中，Chirp Scaling因子的补偿相位误差Δφ1以及距离补偿因子的补偿相位误差Δφ2非常小，而方位补偿因子的补偿相位误差Δφ3随ΔR的变化较明显，找到相位误差Δφ3为π／2时所对应的横坐标值作为ΔR上限的粗略估计，在本文中ΔR≤720。

2）更新步长上限的精确确定

为了更精确地确定ΔR的范围，下面采用实验分析的方法对ΔR作进一步的分析。实验分析的具体步骤是：首先根据表1所列的参数产生点目标回波模拟数据，回波波形如图5 所示，数据粒度为2048×4096（方位向×距离向），然后改变更新步长ΔR，并在加窗情况下分别对点目标进行成像处理，最后对点目标成像结果进行评估，得到ΔR的变化对成像结果的影响，从而确定更新步长。

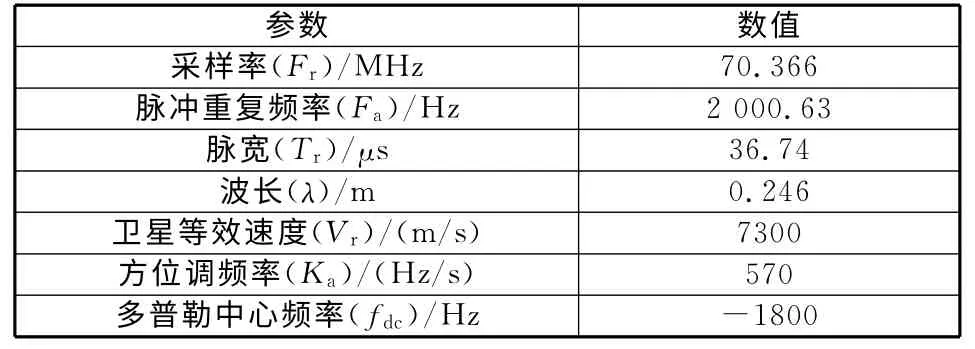
表1 卫星实验参数列表Table 1 List ofexperimental parameter

分别令更新步长ΔR＝1，2，4，8，16，32，且补偿因子在奇数位置进行更新，即距离线更新位置为

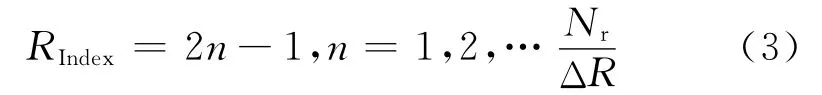
方位线更新位置AIndex为

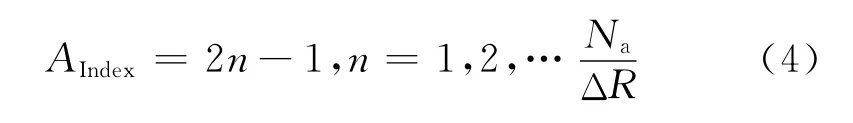
式中：Nr和Na分别为距离向数据长度和方位向数据长度。

在加窗的情况下，当更新步长ΔR＝1时，其点目标成像结果以及距离向和方位向的峰值曲线如图6所示，用不同的更新步长对点目标进行成像，其成 像结果评估统计表如表2、表3所示。

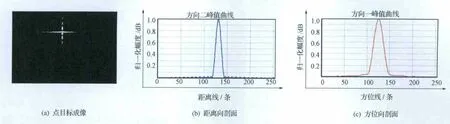
图6 点目标成像结果及峰值曲线Fig．6 Imaging result of point target ＆curve of peak value

表2 点目标成像结果评估表（距离向）Table 2 Evaluation result of point target（range）

表3 点目标成像结果评估表（方位向）Table 3 Evaluation result of point target（Azimuth）

按照以上两组实验得到的点目标成像结果评估表可以作出峰值旁瓣比、积分旁瓣比、空间分辨率与ΔR的变化曲线，如图7所示。从图中可以看出，当ΔR≤32 时，点目标成像结果的三个典型指标的变化都非常小，特别是当ΔR≤16时，其峰值旁瓣比、积分旁瓣比的变化范围更小，而且空间分辨率指标也能满足系统的要求，所以在补偿因子区域不变的CS算法流程中，此时更新步长可以定义为：ΔR∈［0，16］，其中ΔR为偶数。

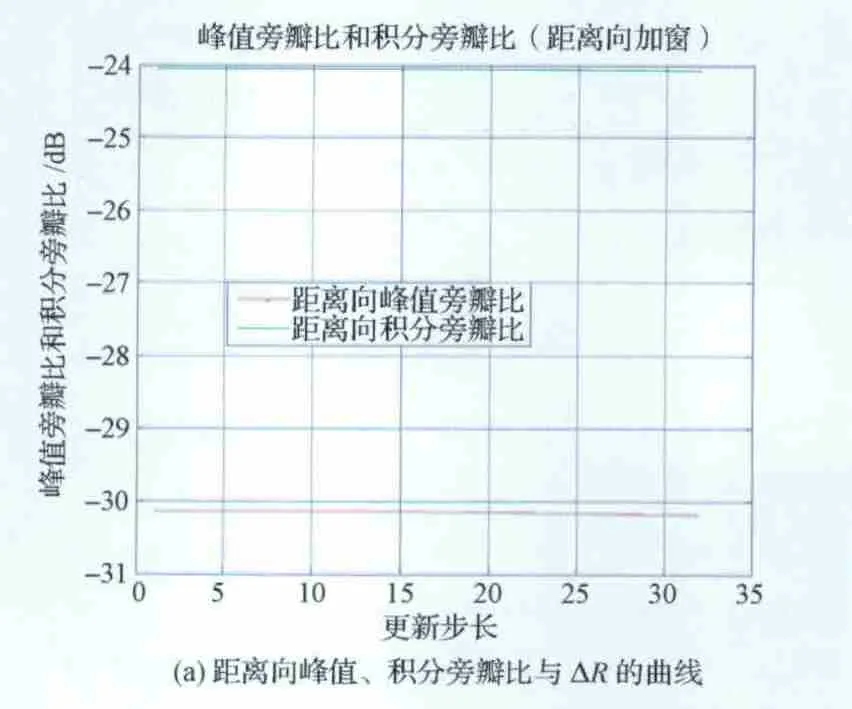
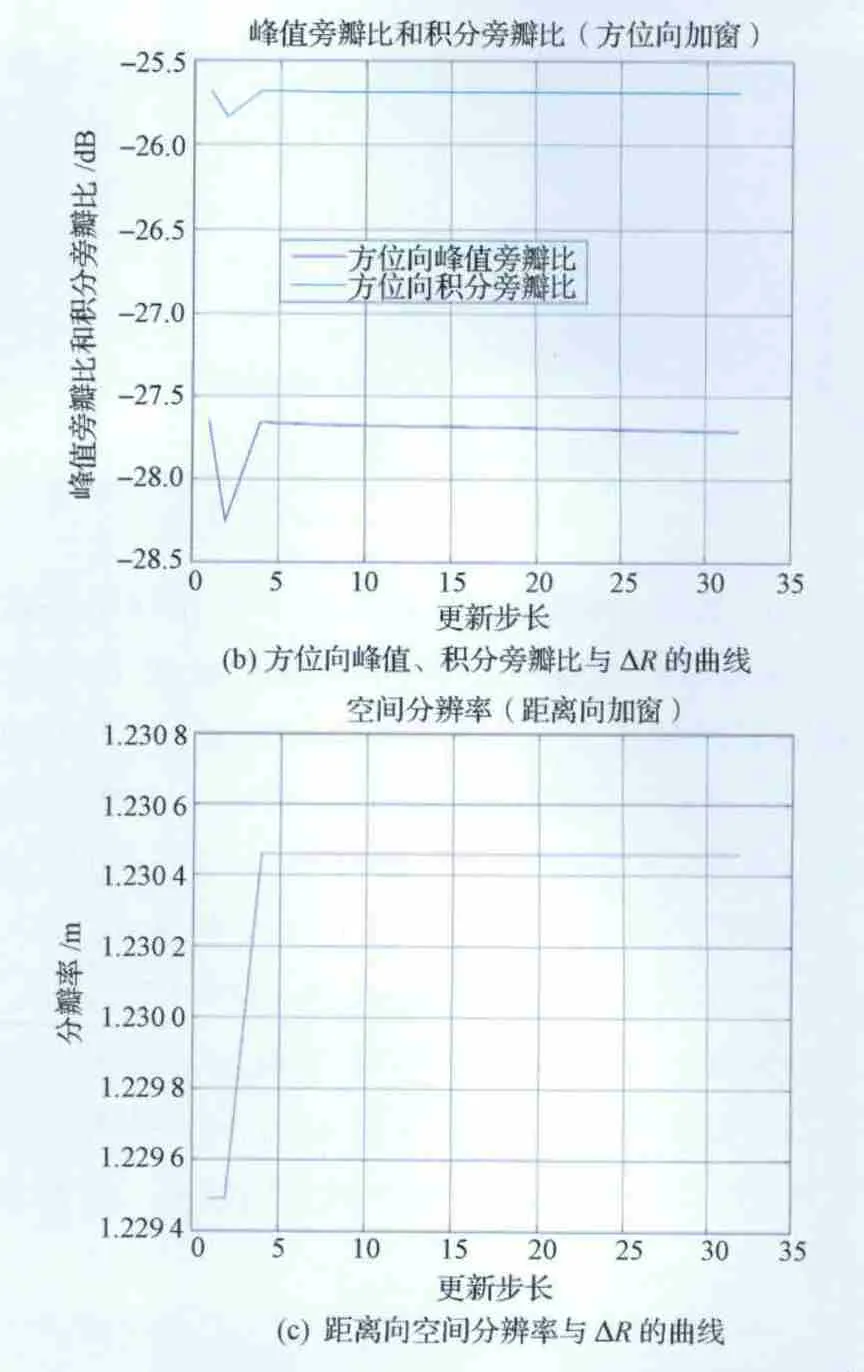
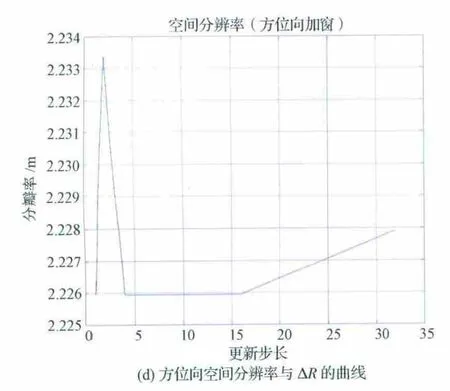
图7 峰值旁瓣比、积分旁瓣比、空间分辨率与ΔR 的变化曲线Fig．7 Variation curve between PLSR，ILSR，resolution and the updating step

6 仿真数据成像结果

由第5章的讨论可知，补偿因子区域不变CS算法的更新步长ΔR的范围为ΔR≤16，现在令ΔR＝16，并对点阵进行成像。

根据表1所示的卫星参数列表，50×50点阵仿真的成像结果如图8所示。

图8 点阵成像结果Fig．8 Imaging result of point array

由成像质量评估结果可知，基于补偿因子区域不变的CS算法的成像质量在图像的近距、中距和远距都满足分辨率（5m×5m）、峰值旁瓣比（-25dB）和积分旁瓣比（-15dB）的质量指标要求。在补偿因子区域不变的CS成像算法中，补偿因子的计算时间减小为原来的1／ΔR，为了评估整个成像处理时间，在配置有Intel（R）Core（TM）i3CPU M380＠2．53GHz双核处理器、2Gbyte内存的计算机上，用MATLAB软件对不同场景大小的图像分别用本文提出的方法和传统的CS成像算法进行处理，并记录它们各自的处理时间，如表4所示。

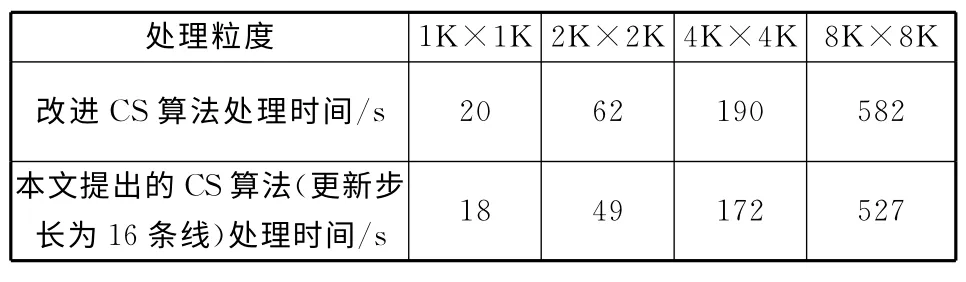
表4 SAR 成像处理时间测试与对比Table 4 The comparison of SAR processing time

从上面的成像处理时间对比表可以看出，补偿因子区域不变的CS算法的成像处理时间比原来的改进CS算法要少，而且随着处理粒度的增大，其成像处理时间减少的会更多。

综上所述，在星载SAR 成像处理中，可以按照前文所述的方法对补偿因子区域不变CS算法的更新步长进行确定，其中主要包括更新步长的粗估计与精确确定，最后只要成像质量的损失在系统可接受范围之内，就可以以一定的步长对补偿因子进行更新，从而成倍地减少补偿因子的计算量，提高成像处理的实时性。

7 结束语

RD、波束域、CS三种经典的SAR 成像算法各有优缺点，单从运算量来看，CS算法具有一定的优势，因此，本文对CS算法进行了研究，提出了一种补偿因子区域不变的CS 成像算法，它保证成像质量的损失在系统可接受范围的条件下，使补偿因子在一定的距离门内不变，从而有效减少了补偿因子的计算量，提高了SAR 成像处理的实时性。

本文仅仅从SAR 成像处理实时性单方面进行了考虑，随着元器件的高速发展，例如高性能FPGA处理器、DSP处理器和专用集成电路（ASIC）的不断涌现，SAR 成像处理的实时性问题，还只是星载SAR 在轨成像处理需要解决的一个较为简单的问题，更为重要的是，需要从多方面入手，综合考虑各种因素的影响，对SAR 图像质量综合评价后才能得出更加可靠的结论，而这正也是后续进一步深入研究的工作所在。

（References）

［1］魏钟铨．合成孔径雷达卫星［M］．北京：科学出版社，2001

Wei Zhongquan．Synthetic aperture radar satellite［M］．Beijing：Science Press，2001（in Chinese）

［2］张澄波．综合孔径雷达原理、系统分析与应用［M］．北京：科学出版社，1989

Zhang Chenbo．Synthetic aperture radar principle，system analysis and application［M］．Beijing：Science Press，1989（in Chinese）

［3］袁孝康．星载合成孔径雷达导论［M］．北京：国防工业出版社，2003

Yuan Xiaokang．Introduction to the spaceborne synthetic aperture radar［M］．Beijing：National Defence Industry Press（in Chinese）

［4］皮亦鸣，杨建宇，付毓生，等．合成孔径雷达成像原理［M］．成都：电子科技大学出版社，2007

Pi Yiming，Yang Jianyu，et al．Synthetic aperture radar imaging principle［M］．Chengdu：University of Electronic Science and Technology of China Press，2007（in Chinese）

［5］何岷，周荫清，陈杰，等．基于星载平台的SAR 实时成像处理实现方法［J］．宇航学报，2006，27（5）：892-896

He Min，Zhou Yinqing，Chen Jie，et al．Implementation of real-time SAR processing on satelliete based processing system［J］．Journal Astronautics，2006，27（5）：892-896（in Chinese）

［6］郭勐，简方军，张钦，等．基于FPGA 实现的星载SAR实时成像系统研究［J］．计算机研究与发展，2007，44（3）：497-502

Guo Meng，Jian Fangjun，Zhangqin，et al．FPGAbased real-time imaging system for spaceborne SAR［J］．Journal of Computer Research and Development，2007，44（3）：497-502（in Chinese）

［7］胡玉新，丁赤飙，吴一戎．基于ω-k算法的宽测绘带星载SAR 成像处理［J］．电子学报，2005，33（6）：1043-1047

Hu Yuxin，Ding Chibiao，Wu Yirong．The wide swath spaceborne SAR imaging based onω-kalgorithm［J］．Acta Electronica Sinica，2005，33（6）：1043-1047 （in Chinese）

［8］Cumming I G，Wong F H．合成孔径雷达成像-算法与实现［M］．洪文，胡东辉，译．北京：电子工业出版社，2007

Cumming I G，Wong F H．Digital processing of synthetic aperture radar data：algorithms and implementation［M］．Hong wen，Hu Donghui，translated．Beijing：Publishing House of Electronics Industry，2007（in Chinese）

［9］黄岩，陈杰，周荫清．高分辨星载SAR 改进Chirp Scaling成像算法［J］．电子学报，2000，28（3）：35-38

Huang Yan，Chen Jie，Zhou Yinqing．Refine Chirp Scaling algorithm for high resolution spaceborne SAR imaging［J］．Acta Electronica Sinica，2000，28（3）：35-38（in Chinese）

［10］李春升，黄岩．基于ChirpScaling算法的星载SAR 成像处理实现方法［J］．电子学报，1996，24（6）：20-24

Li Chunsheng，Huangyan．Aspaceborne SAR imaging processing algorithm using Chirp Scaling［J］．Acta Electronica Sinica，1996，24（6）：20-24（in Chinese）