开洞填充墙钢框架抗震性能分析

田金 马林 王堃

(长安大学建筑工程学院，西安 710061)

钢结构住宅中的填充墙作为实际工程中最常见的“非结构”构件，在结构设计时往往不考虑其对侧向刚度的贡献，但实际上其作为结构体系的一部分仍参与了地震剪力分配，并与整体框架结构之间协同工作。另外，由于门窗设置的要求需要开洞，而洞口的存在也会对填充墙有一定影响。在设计中若不考虑上述因素，而只是把填充墙作为单纯的非结构构件看待，则导致结构的设计意图与实际的受力情况产生较大的偏差，降低了结构在地震中的安全系数。近年来，钢结构的设计理论取得了较大进展，国内外学者针对围护结构对钢框架整体受力性能的影响展开了一系列研究［1-4］，但对开洞填充墙钢框架结构承载性能和抗震性能的研究还十分有限［5］，因此其受力机理、承载力及抗震方面的研究意义重大。本文通过ANSYS有限元软件建立6个足尺模型，深入研究开洞尺寸和位置等因素对填充墙钢框架力学性能的影响规律，并提出初步的设计建议，对推动钢结构住宅体系产业化发展有重要的意义。

1 有限元模型验证

根据武汉理工大学管克俭博士的试验［6］中的填充墙钢框架试件为原型建立有限元模型。有限元模型中钢框架采用二十节点的SOLID95单元模拟，填充墙采用八节点SOLID65实体单元模拟，填充墙体与钢框架之间的粘结作用通过TARGE170和CONTA174单元的面面接触来模拟，屈服硬化准则选用von-mises屈服准则和随动硬化法则。为保证有限元模型边界条件与试验边界条件一致，约束柱脚所有方向的位移，水平荷载通过位移的方式施加在顶层梁对应的外侧柱面的耦合节点上，再对底层框架梁的平面外方向的位移进行约束，防止其侧向失稳。另外，进行结构非线性求解时，为了保证结果的准确性，打开大变形及应力刚化效应，平衡方程的求解方法采用稀疏矩阵直接法(SPARSE)。有限元分析结果与试验结果对比见图1。

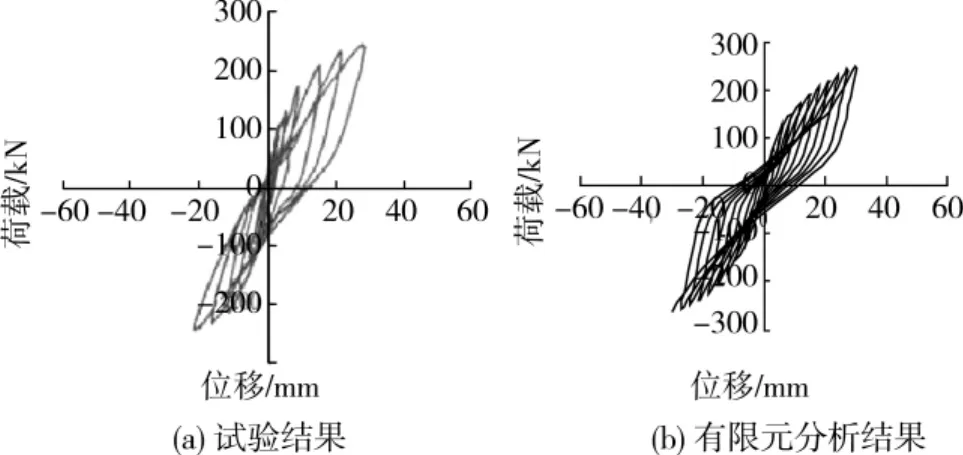
图1 试验结果与有限元分析结果对比图

有限元分析结果和试验结果均出现明显的捏拢现象，只是在反向加载时，有限元分析结果较试验的滞回性能稍强，这主要是由于有限元建模时，填充墙体采用的是整体式模型，没有考虑块体与砂浆之间的粘结现象，使得有限元分析的滞回性能较好。总体而言，本文建立的ANSYS有限元模型能够较好地模拟实际模型在循环荷载作用下的受力性能。

2 有限元模型建立

根据《建筑抗震设计规范》(GB50011-2010)和《高层民用建筑钢结构技术规程》(JGJ99-98)的相关规定，设计一个7层粉煤灰砌体填充墙钢框架结构，依据该工程实例的计算结果，确定基本模型KJ-0试件，并以其为基础通过改变洞口位置和尺寸设计出5个衍生模型。为了避免缩尺模型所产生的一些不利影响，本文所建立的模型均是以该工程实例的计算结果为基础的足尺模型，模型的几何尺寸及立面形状如图2所示。钢框架梁、柱的截面尺寸分别为:300 mm×300 mm×10 mm×12 mm和400 mm×400 mm×12 mm×20 mm，填充墙嵌于钢框架内部，填充墙的尺寸为:6 200 mm×2 700 mm×200 mm。

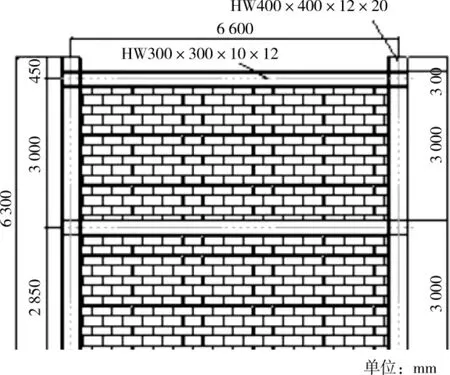
图2 试件的几何尺寸

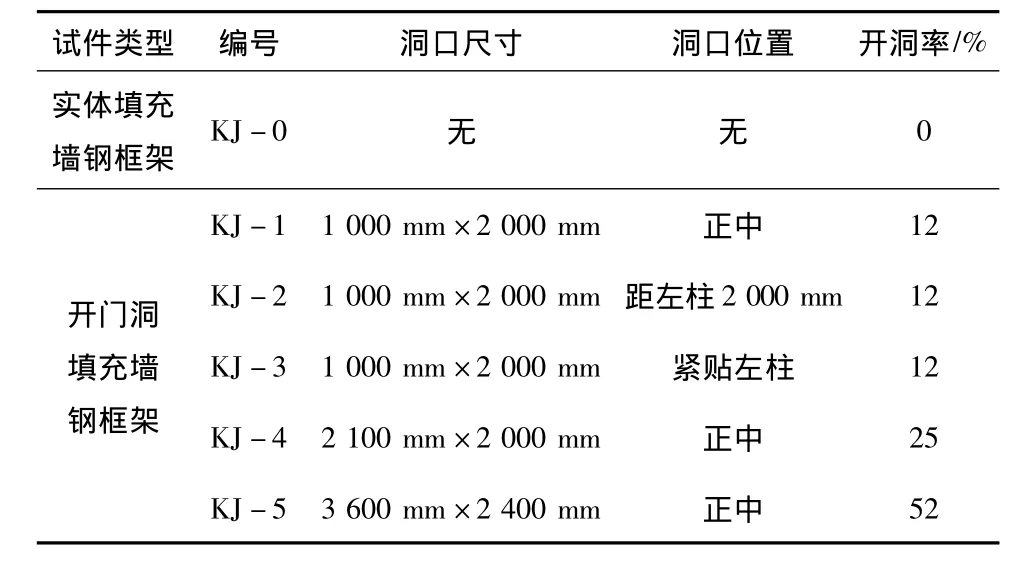
表1 模型参数

实体填充墙钢框架KJ-0的有限元模型如图3所示，梁柱材料均选用Q235，钢材的应力应变曲线采用长安大学卢林枫副教授试验中的钢材材性，应力应变关系见表2。填充墙材料选用蒸压粉煤灰砖，其标称尺寸为240 mm×115 mm×53 mm，通过文献［7］的方法确定出蒸压粉煤灰砖的抗压强度平均值，蒸压粉煤灰砖砌体的本构关系见表3。

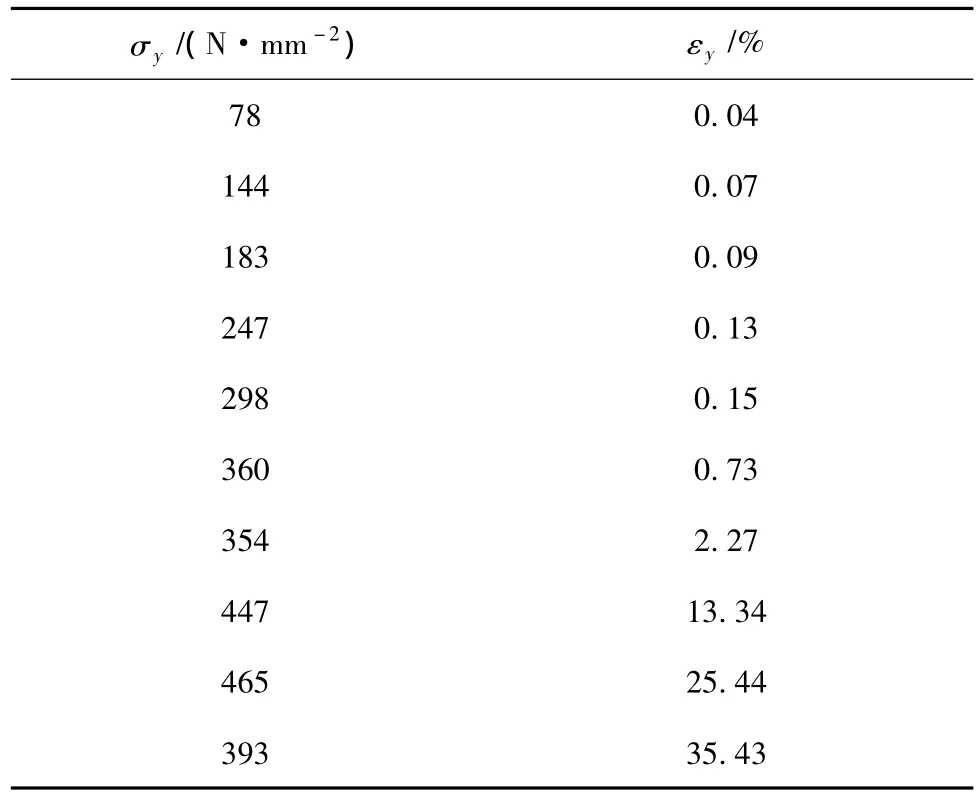
表2 钢材应力应变关系

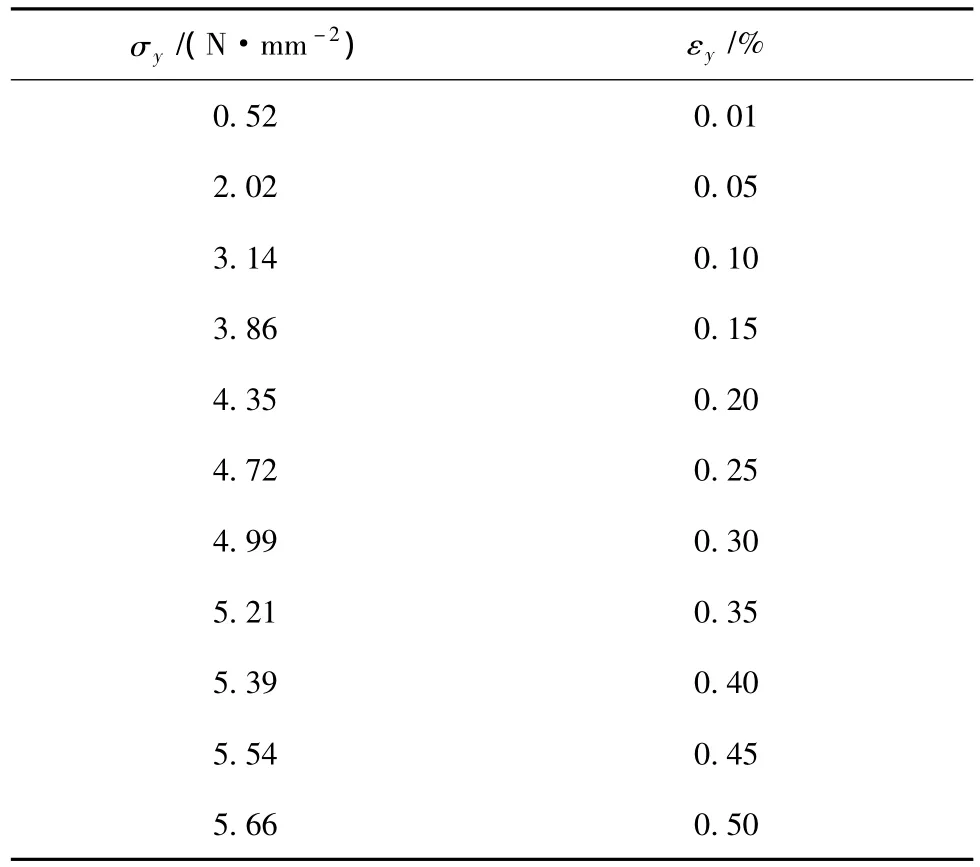
表3 蒸压粉煤灰砖砌体的应力应变关系

3 开洞填充墙钢框架受力性能分析

3.1 极限承载力

有限元分析结果的相关数据见表4。填充墙体洞口的存在降低了整个结构的承载能力，但是洞口位置的改变以及洞口大小的变化对结构的承载能力有不同的影响。

仅考虑洞口位置改变时，KJ-2的极限承载力虽然小于KJ-1的极限承载力，但两者变化不大，而KJ-3的承载力较前两者降低很多。这主要是由于KJ-3模型洞口紧贴左柱，导致填充墙体与钢框架之间的摩擦面减小，降低了填充墙与钢框架之间协同工作的性能，严重影响了其承载力。填充墙体中洞口位置的改变对开洞填充墙仅考虑洞口尺寸的变化时，对比 KJ-0、KJ-1、KJ-4、KJ-5 的相关数据可知，随着开洞面积的增大，结构的承载力不断下降，填充墙体对钢框架的支撑作用逐渐降低，钢框架对钢框架的极限承载能力有一定的影响，但影响程度不及填充墙体与钢框架的接触面积的改变大。

墙体的约束作用也逐渐下降，开洞填充墙与钢框架整体的协同工作性能下降。KJ-1模型的开洞率为12%，极限承载力下降为未开洞KJ-0模型的70.5%，KJ-4模型的开洞率为25%，极限承载力降为KJ-0模型的67.8%，开洞率达到52%的KJ-5模型极限承载力下降最为严重，仅为KJ-0模型的58.5%。

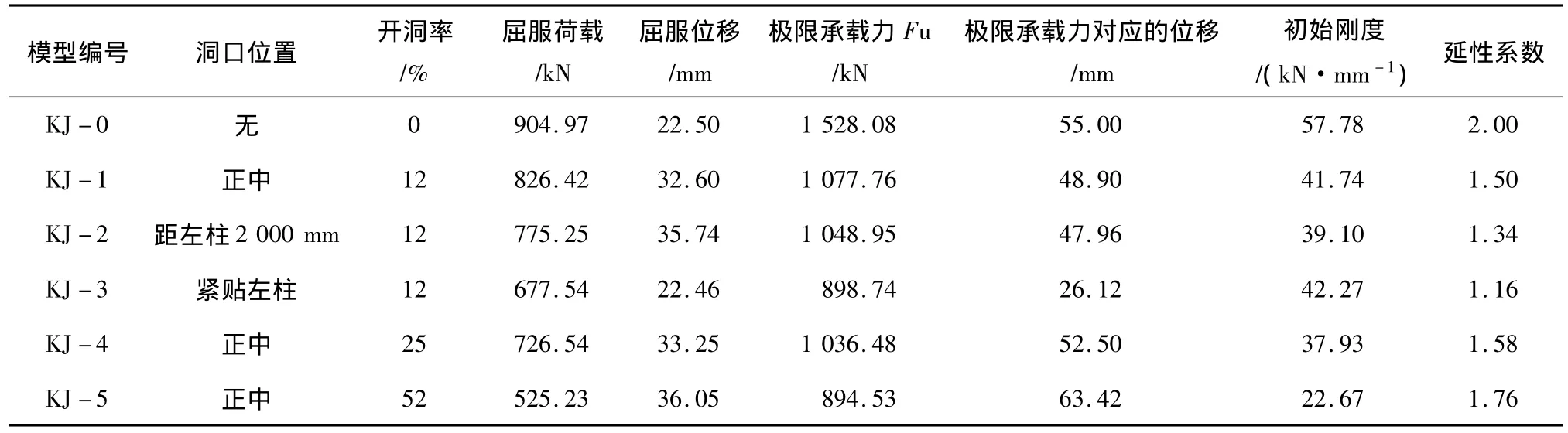
表4 循环荷载作用下试件的力学性能

3.2 滞回性能

模型在低周反复荷载作用下的滞回曲线见图3。填充墙洞口的存在一定程度上削弱了框架的承载能力，也影响了结构的滞回性能，耗能能力也出现了下降。

由图3(b)、(c)、(d)可知，当只考虑洞口位置的影响时，模型的滞回曲线均呈现出比较典型的反S形，说明模型存在明显的捏缩效应，填充墙与钢框架之间存在明显的滑移现象。KJ-1模型和KJ-2模型的滞回曲线相似，而KJ-3模型则与前两者有较大不同。KJ-3模型受到水平推力时的承载力要远大于受到水平拉力时的承载力，这是因为KJ-3模型的洞口紧贴左柱且位于柱下端，在受到水平拉力时，除了对角线范围内墙体的削弱降低了承载力外，填充墙体与钢框架之间接触面积的减小也影响两者之间的协同工作性能;因此，应该尽量避免洞口紧贴钢柱的情况出现，这会极大地降低结构的抗震性能。

对比图3(a)、(b)、(e)、(f)的滞回曲线可以看出，当只考虑洞口尺寸的影响时，模型的滞回曲线除了极限承载力逐渐降低之外，同时存在明显的滑移现象，滞回曲线呈反S形，但开洞率达到52%的KJ-5模型的滞回曲线则呈纺锤形。由此可知，随着开洞率的增大，滞回曲线有逐渐发展成为纺锤形的趋势。这是由于随着开洞面积的不断增大，填充墙对结构的侧向刚度贡献越来越小，整个结构的受力情况越来越接近纯钢框架模型，即承载力逐渐减小，而延性则得到了提高。

3.3 耗能能力

耗能能力是结构抗震性能的一项重要指标。结构的耗能能力以结构在低周反复荷载作用下的滞回环所包围的面积来度量。根据《建筑抗震试验方法规程》(JGJ101-96)的规定，通过定义的能量耗散系数E来反映结构的耗能能力，试件的耗能能力见表5。

在低周反复荷载作用下，填充墙开洞会导致结构耗能能力的变化，具体来讲，其中KJ-1模型下降程度最小，KJ-3次之，KJ-2最大，这主要是因为洞口位置的改变一方面削弱了对角线区域内的填充墙体面积，另一方面加剧了填充墙体的应力集中现象，最终导致开洞模型的耗能能力普遍下降。

对比不同开洞率模型的耗能系数可知，当开洞位置一定时，模型的耗能能力随着洞口面积的增大而增大，这主要是由于洞口面积越大，填充墙体对整个框架体系的影响就越小，结构的变形和耗能能力逐渐趋近于纯框架。

图3 试件滞回曲线

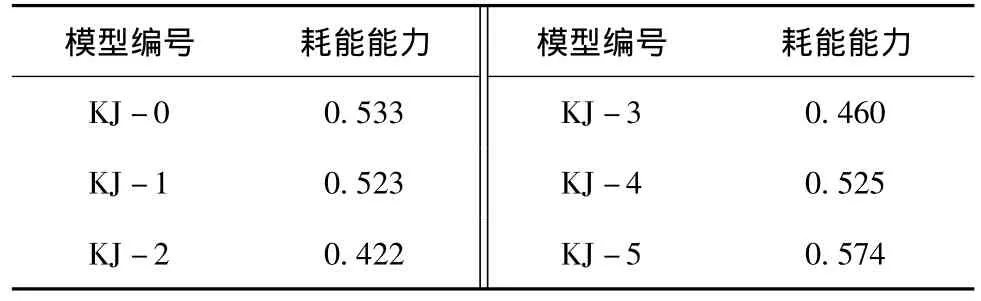
表5 模型耗能能力

4 结论

本文通过ANSYS有限元软件建立钢框架模型，并与试验结果进行对比，验证了有限元模型的正确性。通过改变洞口位置及尺寸，建立了6个足尺开洞粉煤灰砌体填充墙钢框架模型，研究了开洞填充墙钢框架在低周反复荷载作用下的极限承载能力及抗震性能，得出了以下结论:

(1)门窗洞口的存在对结构的承载能力和抗震性能有很大影响。填充墙钢框架开洞后其承载力明显降低，抗震性能也有一定降低，但随着开洞面积的增加钢框架的延性有所改善。

(2)填充墙体中洞口位置的改变对开洞填充墙钢框架的极限承载能力有一定的影响，但影响程度不及填充墙体与钢框架的接触面积的影响显著。当门洞口位于柱端时，由于填充墙体与钢框架接触面积的减小，结构的承载能力明显下降，延性性能劣化明显，因此，应尽量避免洞口位于柱端的情形。

(3)当洞口位置一定时，随着洞口面积的不断增加，开洞填充墙与钢框架整体协同工作性能逐渐降低。因此，随着洞口面积的增大，结构的极限承载力减小，但结构的延性却得到改善，结构的变形和耗能能力均得到提高。因此，在填充墙钢框架设计时，应综合考虑其洞口尺寸对结构承载力和抗震性能的影响。

(4)本文研究中只考虑了填充墙与钢框架的组合作用，对于其他构件，如现浇楼板的组合作用对结构体系的影响，还有待进一步研究。

［1］刘玉姝，李国强.带填充墙钢框架结构抗侧力性能试验及理论研究［J］.建筑结构学报，2005，26(3):78-84.

［2］Kaltakci M Y，Korkmaz H H，Koken A.An Investigation of Behaviour of Steel Frames with Masonry Infills under Lateral Loading［J］.Journal of Engineering and Applied Sciences，2007，2(5):930-943.

［3］郭子雄，吴毅斌，黄群贤.砌体填充墙框架结构抗震性能研究现状与展望［J］.地震工程与工程震动，2008，12(6):172-177.

［4］Amir S D.A Study of the Effect of Infilled Brick Walls on Behavior of Eccentrically Braced Frames Using Explicit Finite Elements Method［J］.American J of Engineering and Applied Sciences，2009，2(1):96-104.

［5］崔名相，陈向荣，周剑，等.填充墙开洞情况对填充墙-钢框架受力性能影响的研究［J］.河南建材，2010(4):42-43.

［6］管克俭.钢结构住宅抗侧力体系试验研究与非线性分析［D］.武汉:武汉理工大学，2003.

［7］秦士洪，倪校军.蒸压粉煤灰砌体应力应变全曲线研究［J］.建筑结构学报，2010(8):94-100.