利用Hudson裂隙模型分析井径变化对声波测井响应的影响

张雪昂，王祝文，韩春江，向 旻，杨 闯

吉林大学地球探测科学与技术学院，长春 130061

0 前言

自然条件下，地壳的变化所产生的力使地层结构发生了复杂的变化，于是不同性状的介质体产生了，裂隙介质便是其中的一种。因为应力具有一定方向性，所以这些裂隙也有一定的走向，于是形成了地层介质的各向异性。这种各向异性的成因主要是裂隙的各种特征属性的差异存在，同时，裂隙性地质结构又是重要的油、气储层环境。因此，通过分析这些裂隙属性所产生的各向异性变化规律，便可以对地层中各种自然资源的价值做出科学判断，这对油气资源的发掘利用、地下水的开采、环境污染的妥善处理等环境资源问题有着相当重要的意义［1］。

早在20世纪80年代，White等［2］、Chan等［3］以及Paillet等［4］便作出了对于各向异性介质中弹性波传播规律的初步研究；但是在这些研究中，并没有对围岩的各向异性参数作出分析。而Hudson［5］、Crampin等［6－8］、蔡晓刚等［9］、Liu等［10］却在地层介质的各向异性的产生原因和特征属性等方面作出了系统研究，同时提出了各向异性参数的概念。 之后，Thomsen［11］、Sinha 等［12］和Tang等［13］提出了裂隙组的特征属性并研究了介质各向异性间的关系。Tichelaar等［14］提出了测定裂隙介质中裂隙组方位角的方法，但此方法只是针对近似垂直裂隙效果尤为明显。目前，最为普遍应用的裂隙理论模型有Hudson理论模型和Thomsen理论模型。Thomsen理论模型的背景设定为裂隙、孔隙、孔洞都为等压分布的理论介质，并且它们的尺度相当［15－16］，同时此模型所采用的各向异性参数是针对于拥有单一对称轴的弱各向异性介质的。在Hudson理论模型中［17］，设定模型背景为：裂隙尺度与其中传播的波长相比要小得多；裂隙分布均匀；裂隙彼此之间无连通，且分布稀疏；裂隙总体积较基质总体积小得多；裂隙形态呈扁球状。在此模型背景中Hudson加入了弹性入射波，并提出了裂隙弹性模量的一阶和二阶扰动量。裂隙介质中，虽然与其中传播的弹性波波长相比，裂隙尺度极小，但裂隙系统的总体表面积较大；因此裂隙群对地层性状的影响不容忽视。目前人们对裂隙对弹性波衰减性影响的研究主要有2种方法：一种是以自然条件为背景做出响应的实物模型，并在此种模型上进行仪器测量从而得出裂隙介质中弹性波的传播规律；另一种是通过计算机以及程序编写模拟出数值裂隙模型，同时数值模拟出其中的弹性波传播作用，从而得出相关的传播规律［18－19］，但是对裂隙介质较为全面的数值模拟分析并不多见。在实际声波测井过程中，对于不同的井孔来说，因为钻头等因素的改变，井眼大小也相应不同，这便给测井解释带来了一定程度的困难。为了分析井眼的变化对声波测井结果的影响，笔者以Hudson裂隙理论模型为研究背景，对变化井径的井孔裂隙介质中传播的声波进行规律性数值模拟分析，结果包括了裂隙各种参数（角度、纵横比、数密度）以及对应井径大小变化的各种测井声波响应，希望对实际的测井勘察应用提供相应的理论分析依据和指导性建议。

1 Hudson裂隙模型数值模拟

Hudson裂隙模型理论中，较为关键的内容在于其提出了裂隙介质的等效弹性模量。笔者在对裂隙介质弹性模量的应用中，引用了Hudson等人的相关裂隙理论［20－24］，进而通过计算得到了 Hudson裂隙介质的综合等效弹性模量［24－25］：

式中：C0是各向同性介质模量；C1是一阶修正量。在Hudson裂隙模型理论中，裂隙呈“硬币”状，设定裂隙面与水平面夹角为φ，下文称之为“裂隙角度”。裂隙群组中的裂隙都有统一的纵横比、半径值。针对以上裂隙介质条件，Hudson提出以下等效弹性模量表达式：

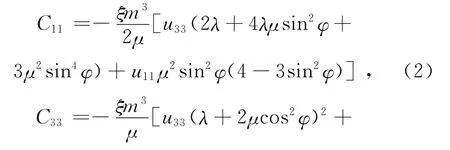
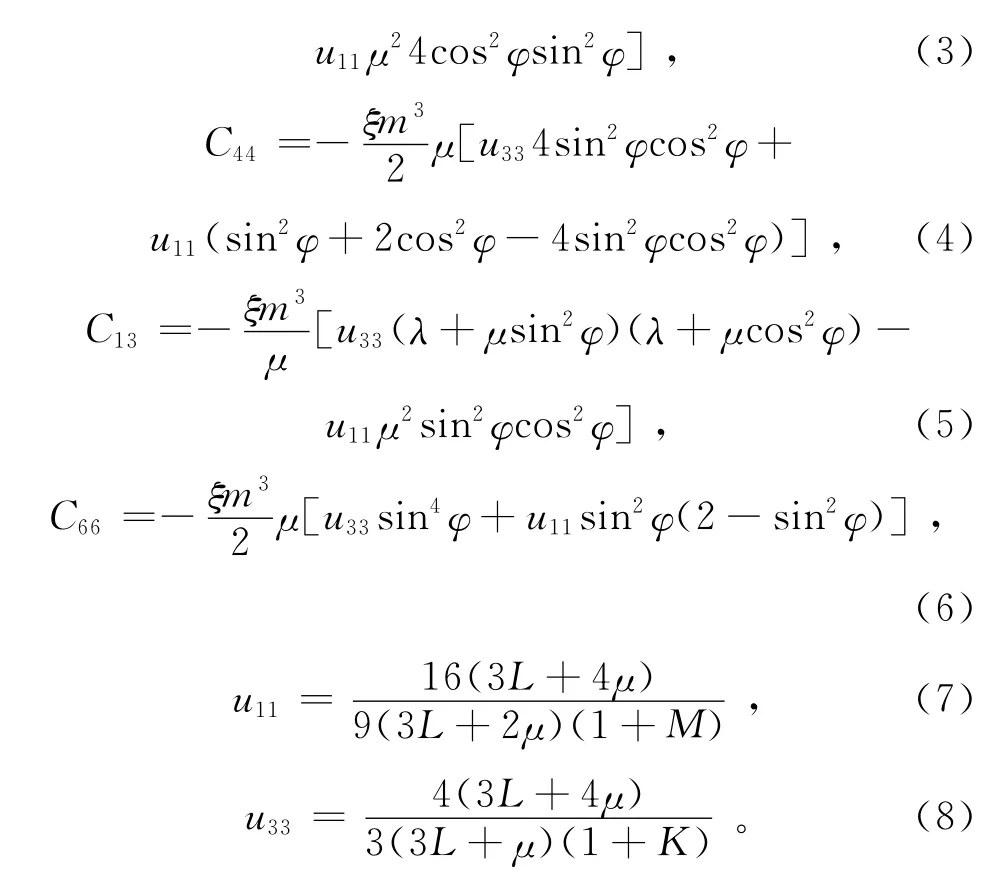
式中：ξ是裂隙数密度；m是裂隙半径；λ和μ是无裂隙岩石的拉梅常数；；M是流体黏滞系数以及裂隙纵横比的函数；K是流体的体积模量、围岩孔隙度以及未损坏岩石渗透率的函数。

通过以上公式，得到此裂隙介质的黏弹参数A、B、C、D、E：

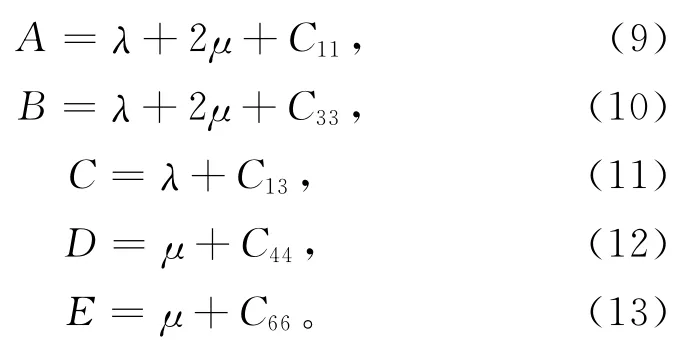
因为井中的接收器所接收到的波动脉冲信号是以声压场的形式体现的，所以想要得到声波测井全波列曲线，需要从声波压力场公式着手。井中的声波压力场公式如下：

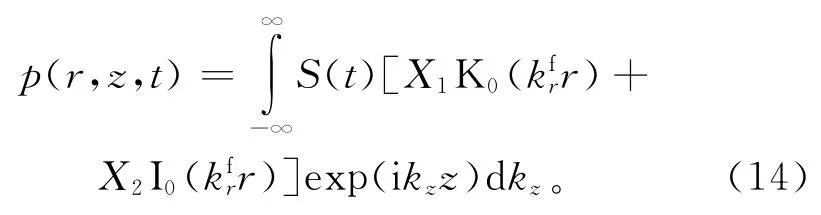
式中：S（t）为声源的函数表达式；X1为与脉冲声源相关的系数；K0为第二类零阶虚宗量贝塞尔函数；I0是第一类零阶虚宗量贝塞尔函数；X2是由角频率和径向波数决定的系数，通过加入边界条件计算便可以得到，X2也叫井孔格林函数（地层滤波函数），综合反映了地层介质的特性，运载信息量丰富；是井孔内流体波数 的径向分量；kz是波数k的轴向分量；ω为脉冲声源的角频率；υ为井孔中的声波波速。

裂隙介质的波动方程［26］为：

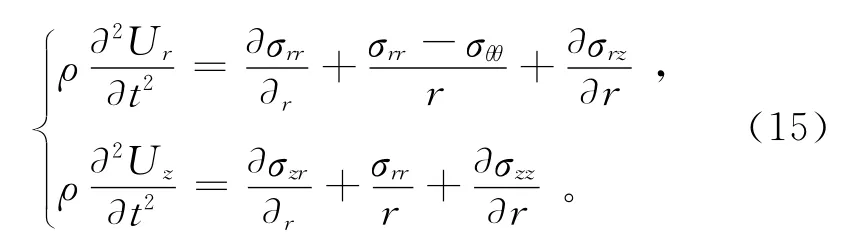
式中：ρ是井孔外空间介质的密度；Ur和Uz分别是位移矢量的径向分量、轴向分量；σ是应力张量。公式（15）的解可以通过一个标量位和一个矢量位的和来表示：

实际情况是，井中的泥浆中含有入射波以及反射波，井外空间的介质中只存在折射纵波以及横波。由此可知，入射波波幅在井轴处数值达到最大值，随着与井轴距离的增加，其幅度值随之减小。而反射波波幅在井壁处达到最大值，随着向井内传播的过程其幅度值逐渐减小。同时折射波在井壁处幅度达到最大，随着波动向地层传播，幅度也随之减小。通过以上情况可知井内流体与井外空间介质中的纵波以及横波的波动方程，进而应用分离变量法求解，便得到了波动方程的解。

将式（16）和式（14）联立，代入边界条件：径向位移连续、径向应力连续、切向应力为0，便可以求出理想裂隙介质模型下的地层滤波系数X2；继而通过实轴积分法进行数值模拟，便可得到裂隙介质条件下的全波列测井曲线。全波列测井曲线中包含了种类较全面的波形，其中主要包括纵波、横波、斯通利波以及伪瑞利波［27－29］。在实轴积分法的计算过程中，笔者采用短时傅里叶变换算法（FFT），这样可以很好地缩短计算时间。计算后得到了时域上的不同时间波形的离散值，因此，实轴积分法也被称为离散波数法［30］。

2 不同井径下数值模拟结果

笔者在Hudson裂隙理论模型介质的基础上，通过改变井径大小以及裂隙参数来模拟不同井径、不同裂隙条件下的声波传播规律，从而为实际应用提供指导参考。设定井眼半径为0.03～0.14m，每隔0.01m依次递增井孔半径进行作图模拟对比，同时改变裂隙参数（角度、数密度、纵横比），最终得出井孔裂隙介质对井径变化响应的全面分析结果。

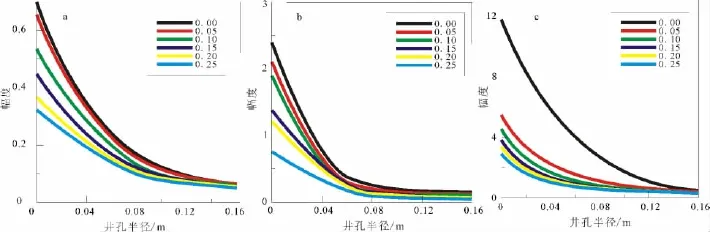
图1 不同裂隙数密度下井孔半径与声波幅度Fig.1 Wellbore radius and wave amplitude with different crack number density

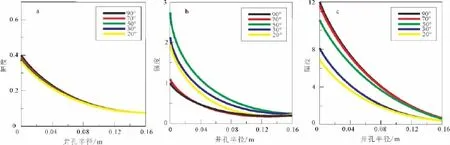
图2 不同裂隙角度下井孔半径与声波幅度Fig.2 Wellbore radius and waves amplitude with different crack angle

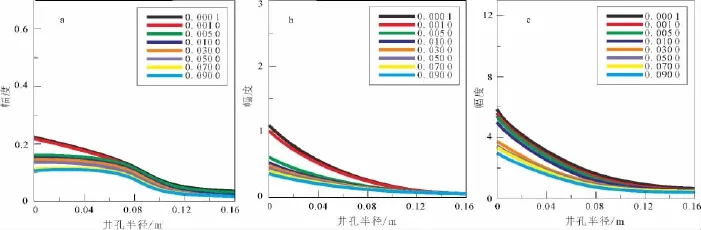
图3 不同裂隙纵横比下井孔半径与声波幅度Fig.3 Wellbore radius and waves amplitude with different crack aspect ratio

图1为在不同裂隙数密度下井孔半径与声波幅度的关系图。从图1中可见，不管是纵波、横波还是斯通利波，它们的幅度都随着井孔半径的增大而产生不同程度的衰减。并且，裂隙数密度越小，声波对井径变化的响应越敏感。随着裂隙数密度的递增，纵、横波幅度下降拐点所对应的井径值也逐渐增大。与纵、横波相比，斯通利波幅度的衰减程度最严重；当裂隙数密度递增到0.05时，斯通利波幅度对井孔半径变化的响应灵敏度出现大幅下降，即裂隙数密度0.05是斯通利波幅度对井孔半径的响应灵敏度的拐点所在。

图2为在不同裂隙角度下井孔半径与声波幅度的关系图。由图2可知，裂隙角度对纵波幅度的影响较弱，整体区分特征极小。对于横波而言，当井孔半径递增时，中、低角度的裂隙中横波幅度整体下降程度明显，但下降趋势逐渐变缓，井孔半径大于0.06 m之后，横波幅度几乎不再下降；高角度裂隙中横波幅度则对井孔半径响应程度很低，随着井孔增大，横波幅度也只有微小程度的减少。可见，横波幅度在中、低角度裂隙中对井孔半径的响应较敏感。伴随着井径的增大，裂隙介质中的斯通利波幅度都有比较明显的衰减现象，其中，中、高角度裂隙中的斯通利波幅度衰减更加严重。这说明，对于斯通利波的幅度而言，其在中、高角度裂隙中对井孔半径的响应更加敏感。

图3为在不同裂隙纵横比下井孔半径与声波幅度的关系图。由图3可知，声波幅度随井孔半径递增逐渐下降，下降趋势愈发平稳，下降速率趋于0。裂隙纵横比较小时，纵、横波以及斯通利波幅度衰减程度较严重。可见，裂隙纵横比越小，声波对井孔半径的响应越敏感。对纵、横波而言，裂隙纵横比大于0.001之后，纵横比对幅度衰减的区分性变小。对斯通利波而言，裂隙纵横比大于0.01之后，幅度下降程度明显减小，即纵横比0.01是斯通利波幅度对井孔半径的响应灵敏度的拐点所在。

图4为井孔半径为0.04～0.14m（每隔0.02m依次递增）的井孔二维谱。图4中：1号线代表泥浆波，斯通利波谱值紧挨泥浆波谱值，分布于低频区域，即图中靠近0点的黑色三角状区域，速度接近泥浆波波速，频率分布范围随井孔半径增大而减小；2号线代表地层横波；3号线代表地层纵波；3条线的斜率代表对应波的慢度（波速的倒数）；横坐标轴与3号线之间的谱值代表纵波的泄漏模式，2号线与3号线之间的谱值代表横波的泄漏模式，1号线与2号线之间的谱值代表伪瑞利波。通过观察图4可知，3条线的斜率并不随井径的变化而改变，可知井径不影响纵波、横波以及斯通利波的波速。图中暗色条纹代表各种频散性波动的模式状态［31］，每个条纹所对应的频率即为各种波的激发频率。通过图4可知，随着井孔半径增大，波动的最小激发频率减小，激发强度峰值所在频率带向低频区域移动。在相同频率范围内，井孔半径增大，各种具有频散特征的波动的模式数量不断增多，模式条纹越来越细，截止频率范围变小，同时向低频区域移动。模式条纹变细说明声波中的能量已分散到各个模式之中，声波幅度会有所减小。模式数量增多说明波列成分随井径增大而愈发复杂。

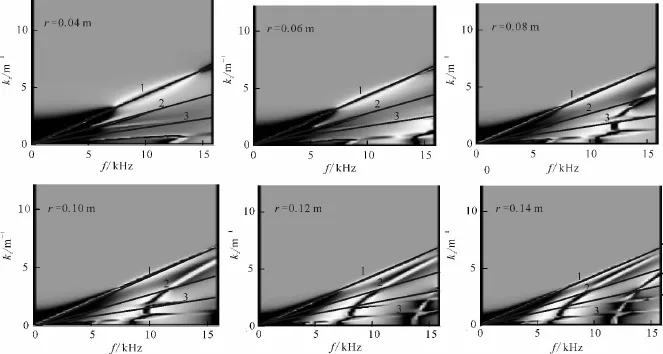
图4 不同井孔半径声场二维谱Fig.4 Different wellbore radius of two－dimensional acoustic field spectrum

3 结论

1）各种波动的幅度随井孔半径的递增产生一定程度的衰减。裂隙数密度较小的介质中纵波、横波、斯通利波的幅度对井孔半径的变化比较敏感。中、低角度裂隙介质中的横波幅度以及中、高角度裂隙介质中的斯通利波幅度对井孔半径的变化比较敏感。裂隙纵横比较小的介质中斯通利波幅度对井孔半径的变化更加敏感。

2）整体而言，声波速度随井孔半径递增的变化不大，即裂隙介质中的声波波速对井孔变化响应不敏感。通过观察频率－波数二维谱可以发现，随着井孔半径的增大，最小激发频率减小，激发强度峰值所在频率带向低频区域移动，频散特征明显的波动模式数量增多，模式条纹变细。声波能量随井径增大分散到各个模式之中，能量损失增多，波列组成成分愈发复杂。

（References）：

［1］刘恩儒，曾新吾.裂隙介质的有效弹性常数［J］.石油地球物理勘探，2001，36（1）：37－44.Liu Enru，Zeng Xinwu.The Effective Elastic Constants of Fractured Media［J］.Oil Geophysical Prospecting，2001，36（1）：37－44.

［2］White J E，Tongtaow C.Cylindrical Waves in Transversely Isotropic Media［J］.Journal of the Acoustical Society of America，1981，70：1147－1155.

［3］Chan A K，Tsang L.Propagation of Acoustic Waves in a Fluid－Filled Borehole Surrounded by Concentrically Layered Transversely Isotropic Formation［J］.Journal of the Acoustical Society of America，1983，74：1605－1616.

［4］Paillet F，Cheng C H.Acoustic Waves in Boreholes［M］.Boca Raton：CRC Press Inc，1991.

［5］Hudson J A.Wave Speeds and Attenuation of Elastic Waves in Material Containing Cracks［J］.Geophys J R Astron Soc，1981，64：133－150.

［6］Crampin S.A Review of Wave Motion in Anisotropic and Cracked Elastic－Media［J］.Wave Motion，1981，3：343－391.

［7］Crampin S.Effective Anisotropic Elastic－Constants for Wave Propagation Through Cracked Solids［J］.Geophys J R Astron Soc，1984，76：135－144.

［8］Crampin S.A Review of the Effects of Crack Geometry on Wave Propagation Through Aligned Cracks［J］.Can J Expel Geophys，1993，29：13－18.

［9］蔡晓刚，姚陈，陈晓非.各向异性ATI介质剪切位错源地震矩张量［J］.地球物理学报，2011，54（7）：1772－1782.Cai Xiaogang，Yao Chen，Chen Xiaofei.Seismic Moment Tensor in ATI Medium，Shear Faulting［J］.Chinese Journal of Geophysics，2011，54（7）：1772－1782.

［10］Liu E，Chanpman M，Varela I，et al.Velocity and Attenuation Anisotropy：Implication of Seismic Fracture Characterizations［J］.The Leading Edge，2007：1170－1174.

［11］Thomsen L.Elastic Anisotropy Due to Aligned Cracks in Porous Rocks［J］.Geophysical Prospecting，1995，43：805－829.

［12］Sinha B，Kostek S.Stress－Induced Azimuthal Anisotropy in Borehole Flexural Waves［J］.Geophysics，1996，61：1899－1907.

［13］Tang X，Chunduru R K.Simultaneous Inversion of Formation Shear－Wave Anisotropy Parameters From Cross－Dipole Acoustic－Array Waveform Data［J］.Geophysics，1999，64：1502－1511.

［14］Tichelaar B W，Hatchell P J.Inversion of 4－C Borehole Flexural Waves to Determine Anisotropy in a Fractured Carbonate Reservoir［J］.Geophysics，1997，62：1432－1441.

［15］Thomsen L.Weak Elastic Anisotropy［J］.Geophysics，1986，51（10）：1954－1966.

［16］Thomsen L.Elastic Anisotropy Due to Aligned Cracks in Porous Rock［J］.Geophysical Prospecting，1995，43：805－829.

［17］Hudson J A.A Higher Order Approximation to the Wave Propagation Constants for Cracked Solid［J］.Geophys J R Astr Soc，1986，87：265－274.

［18］牛滨华，何樵登，孙春岩.裂隙各向异性介质波场VSP多分量记录的数值模拟［J］.地球物理学报，1995，38（4）：519－527.Niu Binhua，He Qiaodeng，Sun Chunyan.Numerical Modeling of VSP Multi Component Records in Cracks Anisotropic Medium［J］.Acta Geophysica Sinica，1995，38（4）：519－527.

［19］陈乔，刘向君，梁利喜，等.裂缝模型声波衰减系数的数值模拟［J］.地 球 物 理 学 报，2012，55（6）：2044－2052.Chen Qiao，Liu Xiangjun，Liang Lixi，et al.Numerical Simulation of the Fractured Model Acoustic Attenuation Coefficient［J］.Chinese Journal of Geophysics，2012，55（6）：2044－2052.

［20］Hudson J A.Overall Elastic Properties of Isotropic Materials with Arbitrary Distribution of Circular Cracks［J］.Geophysical Journal of the Royal Astronomical Society，1990，102：465－469.

［21］Peacock S，Hudson J A.Seismic Properties of Rock with Distributions of Small Cracks［J］.Geophysical Journal International，1990，102：471－484.

［22］Hudson J A，Liu E，Crampin S.The Mechanical Properties of Materials with Interconnected Cracks and Pores［J］.Geophysical Journal International，1996，124：105－112.

［23］Pointer T，Liu E，Hudson J A.Seismic Wave Propagation in Cracked Porous Media［J］.Geophysical Journal International，2000，142：199－231.

［24］Hudson J A，Pointer T，Liu E.Effective－Medium Theories for Fluid－Saturated Materials with Aligned Cracks［J］.Geophysical Prospecting，2001，49：509－522.

［25］Hudson J A，Liu E，Crampin S.The Mechanical Properties of Materials with Interconnected Cracks and Pores［J］.Geophysical Journal International，1996，124：105－112.

［26］White J E，Tongtaow C.Cylindrical Waves in Transversely Isotropic Media［J］.Journal of the Acoustical Society of America，1981，70：1147－1155.

［27］Schmitt B P，Bouchon M.Full Wave Acoustic Logging：Synthetic Micro Seismograms and Frequency Wave－Number Analysis［J］.Geophysics，1985，50：1756－1778.

［28］王祝文，王晓丽，刘菁华，等.裂缝性地层声波测井的联合时频特征［J］.吉林大学学报：地球科学版，2012，42（4）：914－920.Wang Zhuwen，Wang Xiaoli，Liu Jinghua，et al.Joint Time Frequency Characteristics of Array Acoustic Logging Signals on Fractured Formation［J］.Journal of Jilin University：Earth Science Edition，2012，42（4）：914－920.

［29］Kneller L E，Markov M G，Zamaletdinov M，et al.Direct and Inverse Problems of Acoustic Log［M］.Moscow：VIEMS，1991.

［30］Leung Tsang，Dennis Rader.Numerical Evaluation of the Transient Acoustic Waveform Due to a Point Source in a Fluid－Filled Borehole［J］.Geophysics，1979，44：1706－1720.

［31］岳崇旺，王祝文，陈博涛，等.井孔声场二维谱的数值计算与理论分析［J］.吉林大学学报：地球科学版，2009，39（3）：535－540.Yue Chongwang，Wang Zhuwen，Chen Botao，et al.Numerical Calculation and Analysis on Two－Dimensional Spectrum for Acoustic Wave Propagation in a Borehole［J］.Journal of Jilin University：Earth Science Edition，2009，39（3）：535－540.