可倾瓦轴承轴瓦间隙补偿方法探讨

徐纪高， 周礼新， 李艳

（开封空分集团有限公司工艺部，河南开封475002）

1 引 言

可倾瓦轴承的每个瓦块都可绕支点作微量摆动，工作时与转子轴颈形成收敛油楔，并且在运行参数（负荷、速度、润滑油粘度等）改变时，瓦块位置自动调整，使每个瓦块产生的油膜压力都通过支点交汇到轴颈中心，不产生使轴颈涡动的切向分力，有很好的工作稳定性；同时可倾瓦摩擦损失较少、温升较低、承载力适中。在现代高速透平压缩机中得到广泛应用。

我公司生产使用可倾瓦轴承已有多年。本文通过对一种型号的轴承作深入分析，努力找到装配时轴瓦间隙减小的原因及规律，探讨通过间隙补偿方法控制轴瓦间隙，达到不需修刮瓦块的目的。

2 修刮瓦块法——原工艺保证轴瓦间隙方法的介绍与评价

我公司透平压缩机中使用的可倾瓦轴承采用5 块瓦。图1 为一种型号轴承的典型结构：瓦块2 由定位螺钉5 与轴承体1 松动联接，能绕轴承体1 内表面微量摆动；轴承体1 上安装4 块衬板3，由轴承压盖7 通过螺栓6 将其压紧在机身8 上；通过调节下轴承体的3 块衬板垫片4 的厚度，调整轴承中心高及左右位置；通过调节上轴承体衬板垫片4 的厚度，调整轴承压紧力。

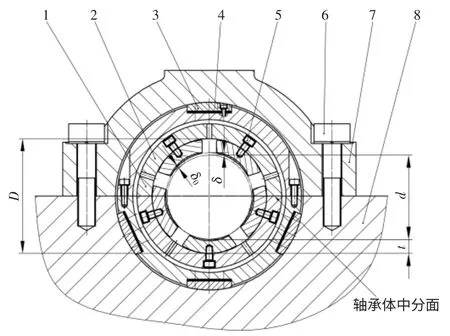
图11.轴承体（上、下） 2.瓦块（5 件） 3.衬板（4 件） 4.衬板垫片（4组）5.定位螺钉（5 件） 6.压紧螺栓（2 件） 7.轴承压盖 8.机身

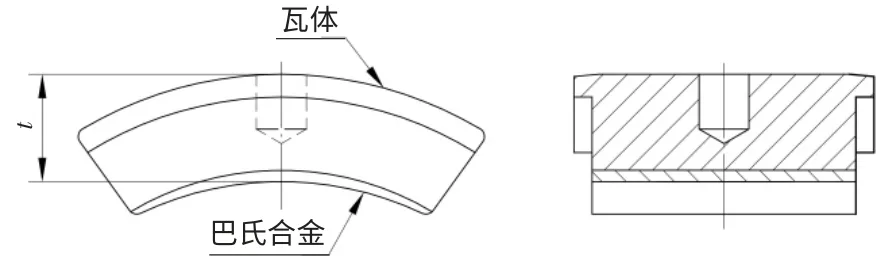
图2

图2 为瓦块结构，内弧为巴氏合金面。此种瓦块结构简单、厚度小、刚性好，在多种型号的轴承中得到使用。

轴瓦间隙δ 是形成油楔的主要参数，也是轴承装配的关键点。理论上，轴瓦间隙由轴承体内径、瓦块厚度、转子轴径等尺寸决定，且5 个瓦块的轴瓦间隙应一致。

图1 中，静止时转子轴颈与下瓦块贴合，上瓦块中心处设计间隙δ0与轴瓦总δ 有如下近似关系：

图纸中设计总间隙δ 在0.21～0.265mm 之间。

由式（2）计算出上瓦块中心处设计间隙δ0在0.191～0.241mm 之间。

对轴承零件加工尺寸进行测量，由式（1）计算出轴瓦理论间隙：δ=0.227mm。

此时，由式（2）计算上瓦块中心处间隙δ0应为：δ0=δ/1.1=0.206mm。

将轴承按设计要求进行装配后，用压铅丝法进行间隙测量（铅丝直径为φ0.3mm）。测得轴承压紧时的上瓦块中心处铅丝厚度为0.178mm。说明装配后轴瓦间隙小于计算间隙。

在上瓦块中心处间隙减小量0.028mm，同时还小于设计最小间隙0.013mm。

为得到轴瓦设计间隙，需要对上瓦块进行修刮，减薄瓦块厚度尺寸t。

修刮瓦块采用两种方法：一是刮削与轴颈配合的巴氏合金面；二是用金刚砂纸和油石修磨瓦块背面。

多年来，我公司一直按这两种传统工艺方法保证轴瓦装配间隙。但是，无论采用哪种方法修刮瓦块，都存在以下缺点：（1）改变了瓦块的原来加工表面；（2）手工修磨瓦块尺寸容易超差；（3）修刮后瓦块失去互换性。因此，用修刮瓦块的方法保证轴瓦间隙，会导致轴承性能下降。必须寻找更好的方法保证轴瓦间隙。

3 轴瓦间隙变化的原因分析

导致轴瓦间隙大小的原因，除了相关零件的尺寸偏差外，还可能与零件的形位公差有关。但是，仔细检查发现，各零件的形位公差远小于标准要求，基本不对轴瓦间隙变化造成影响。

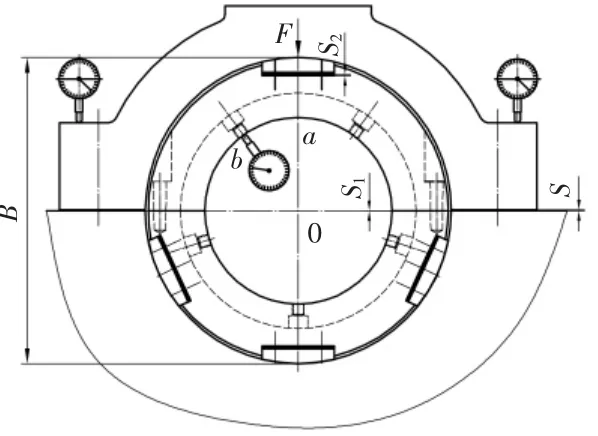
图3

经过进一步分析判断，施加给轴承的压紧力应该是轴瓦间隙减小的主要原因。为保证轴承有充分的刚性承受冲击及交变载荷，在装配时需要对轴承施加一定的经向压紧力。从图3 可以看出，当上、下轴承体中分面贴合（S1=0），增加上轴承体衬板垫片厚度S2，在轴承压盖与机身中分面产生间隙S。拧紧螺栓，消除轴承压盖与机身中分面间隙S，轴承压盖产生对轴承体的压紧力F。因此，S 也叫轴承压紧过盈量。一般情况下压紧过盈量S 由设计给定，对一种型号的轴承来说有一定的范围。本例轴承设计过盈量平均值为0.07mm。

由于轴承盖远比轴承体的刚性好，在压紧力F 作用下，轴承体变形，内表面变为近似椭圆面，在轴承体内径与瓦块背面接触位置b 处产生变形量S0（图4 所示），应该是轴瓦间隙减小的主要原因。但情况到底怎样，还需要通过实际检验证明。

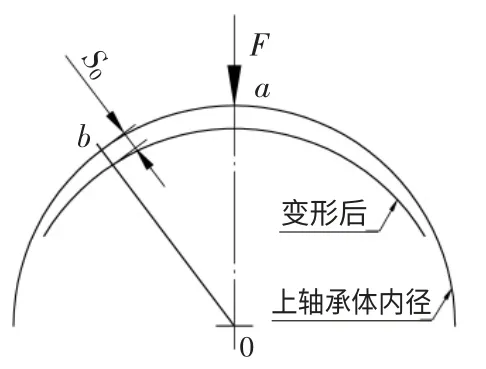
图4

为找出压紧过盈量S 与变形量S0的关系，采用检测方法如图3 所示：先增加上轴承体衬板垫片厚度0.1mm，获得足够的压紧过盈量；将所有瓦块去掉；在轴瓦中心b 处及轴承盖两边压紧面分别架上千分表。首先，拧紧轴承压盖的压紧螺栓，压死轴承压盖，并将3 块千分表调零；然后同步均匀松开轴承压盖两边压紧螺栓，读取、记录各千分表读数。

通过分析记录的千分表数据，得到图5 所示的压紧过盈量S 与b 处变形量S0之间的比例关系，证明了在预紧力作用下轴承体变形是轴瓦间隙减小的直接原因。

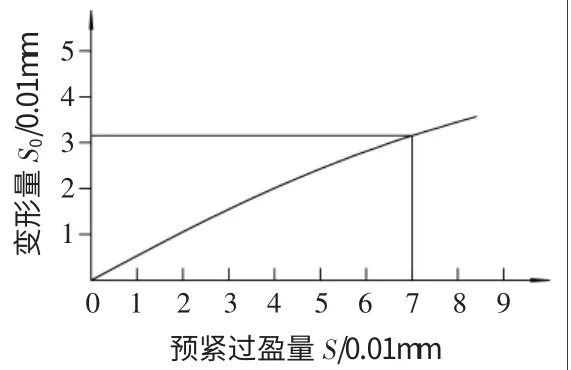
图5

图5 中，轴承体b 处变形量S0与压紧过盈量S 之间近似线性关系为：

K 为变形比例系数。在压紧过盈量0.07mm 附近，该型号轴承K=0.45。

4 间隙补偿法-新工艺保证轴瓦间隙方法的探讨与实践

4.1 间隙补偿法的理论分析

分析轴承工作情况得知，轴承体内表面除瓦块支撑点附近外，其他部位形状变化与轴承能否正常工作关系不大。

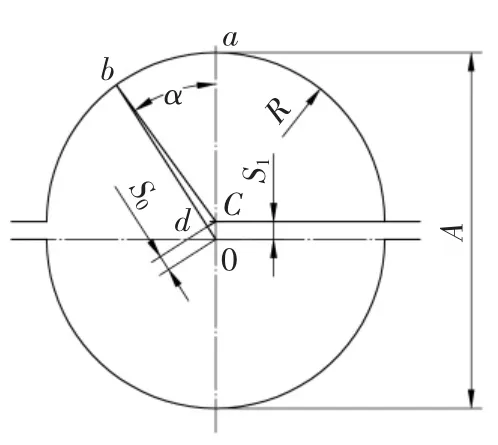
图6

图6 中，S1与轴承体内径R 相比趋于无穷小。因此有：

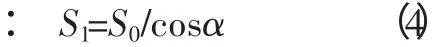
α 为上瓦块定位螺钉与垂直中心线的夹角。

对于一种型号的轴承，α、S 均为已知常量，K 通过实际测量得到，也为常量。应用式（5）、（6）即可分别求得S1、S2。从以上分析可知，运用“间隙补偿法”保证轴瓦设计间隙，理论上是可行的。

鉴于国外对大型科学仪器设备的使用和管理较国内起步早，其对设备开放共享问题的研究、实践、遇到的问题及解决方法均值得探讨和思考。

4.2 间隙补偿法的实际应用

在本例轴承中，α=36°，K=0.45，过盈量平均值为S=0.07mm。进行计算如下：

由式（5）计算上、下轴承体中分面垫片厚度S1为：

S1=K·S/cosα=0.45×0.07/cos36°=0.039≈0.04mm

此时b 处间隙增大量可以由式（3）算出；

S0=K·S＝0.45×0.07=0.0315≈0.03mm

由式（6）计算上瓦衬板垫片增加厚度S2为：

S2=S-S1=0.07-0.04=0.03mm

利用这一计算结果，将上、下轴承体中分面垫上厚度为0.04mm 垫片，将上轴承体衬板垫片厚度增加0.03mm，进行装配压紧。

经压铅丝测量，上瓦块铅丝的最小厚度为0.21mm。达到图纸规定范围0.191～0.241mm。

在生产中，考虑到零件加工偏差，采用下面工艺方法保证轴瓦间隙更为有效：

（1）轴承体精加工后测量其内径D（见图1），用测量结果修正轴承体垫片厚度S1，垫上垫片并将上、下轴承体合上后，测量、校验尺寸A（见图6）；

（2）完成上一步后，测量上、下衬板与轴承室配合尺寸B（见图3），直接调整上衬板垫片厚度S2，保证压紧过盈量S。

5 结 语

（1）对轴承体施加的压紧力是导致轴瓦间隙减小的直接原因。（2）利用间隙补偿原理，抵消压紧变形带来的轴瓦间隙减小，效果很好。是一种保证可倾瓦轴承装配质量的有效方法。（3）由于结构及加工方式不同，应根据实际情况找出不同轴承合适的间隙补偿方法。

［1］ 吴明，孙茂才.可倾瓦滑动轴承间隙的计算［J］.设备管理与维修，2004（1）：19.