随钻自然伽马地层边界模型分析

向长生 王智锋 亢武臣

（1.中国石油大学（华东）石油工程学院，山东青岛 266580；2.胜利石油管理局钻井工艺研究院，山东东营 257017）

国内外油气勘探开发已经进入后期：一方面，老油区存在着大量的边缘油气藏、独立小油气藏、复杂断块油气藏、超薄油气藏等难动用储量；另一方面，新探明储区大多处于地层深处、海洋、滩海、沙漠等地区，特殊的油藏开发条件和复杂的油藏地质结构使得勘探开发成本和难度大大增加，对钻井技术的要求也越来越苛刻［1-2］。传统的钻采技术已经无法从根本上提高采收率和实现对上述难动用储量的油气资源开采。为实现稳产，分支井、水平井、大位移井等新型钻井工艺的应用越来越多［3-4］，对钻井施工过程中控制钻头穿越油藏储层到达靶点的要求越来越高。因此，在随钻测控过程中，准确判断地层边界位置，尤其是准确预测储层边界，对于提高井眼轨迹控制水平和储层有效钻遇率具有十分重要的意义［5］。

笔者利用自然伽马强度分布的基本原理，建立了无限均匀水平地层模型中探测点距离地层边界的解析求解法，对于随钻测井数据解释以及分辨地层具有一定参考价值。

1 随钻自然伽马测量技术

1.1 基本原理

由于任何物体或多或少都含有天然放射性元素，尤其以自然伽马射线穿透能力最强。通过求解地层中自然伽马射线的强度情况，就可以得出所处地层的岩性，如地层的厚度、以及相邻地层的边界等特性，所以在常规LWD 中一般会提供自然伽马测量数据。

1.2 自然伽马强度分布

为简化分析，考虑探测点所在地层为无限均匀，假设探测点所处地层的密度为ρ，每克中含q 克放射性物质，每克放射性物质平均每秒发射a 个自然伽马光子，地层对自然伽马射线的吸收系数为μ。

地层体积元dV 在探测点处形成的自然伽马通量dJv为

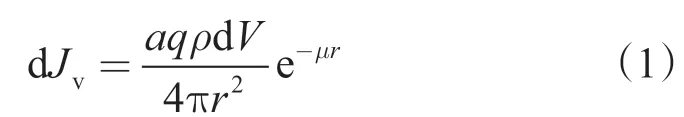
采用球坐标系，dV = r2·sinθ ·d θ d φd r ，则上式写成

对式（2）进行积分后得

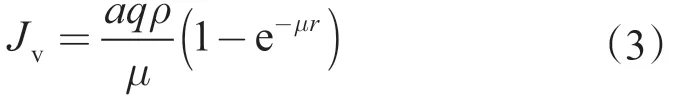
式（3）表示半径为r 的均匀球体空间在球心形成的自然伽马通量。

根据式（3），设探测点处99%的自然伽马通量由半径为R 的球体造成，则有1-e-μr=0.99，由此可得μr=4.065，从而根据不同地层的μ 值算出相应R 值。一般认为自然伽马射线在沉积岩中的平均穿透深度约30 cm，如果考虑套管、钻杆、钻井液等因素影响，R的实际探测深度一般不会超过20 cm［6-7］。

2 无限均匀水平地层中自然伽马强度分布模型

根据式（3），以两无限均匀的水平地层分界面为横轴建立坐标系，如图1 所示：Ⅰ区与Ⅱ区地层参数分别为μ1、a1、q1、ρ1和μ2、a2、q2、ρ2，R1表示自然伽马在Ⅰ区地层通过的距离，R2表示自然伽马在Ⅱ区地层通过的距离，R=R1+R2。

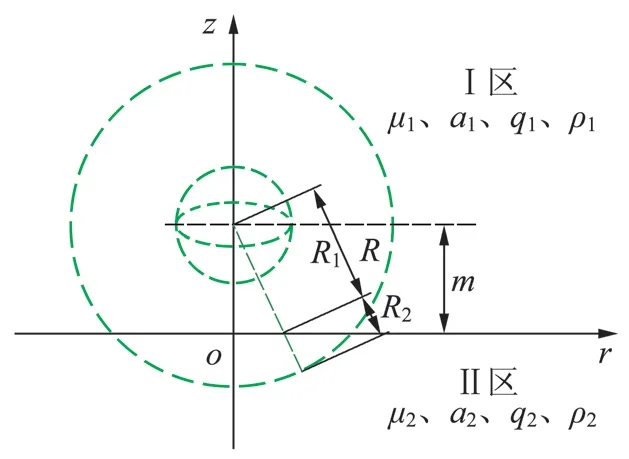
图1 无限均匀水平地层中自然伽马通量计算模型

（1）地层Ⅰ的自然伽马分布

（2）地层Ⅱ的自然伽马分布

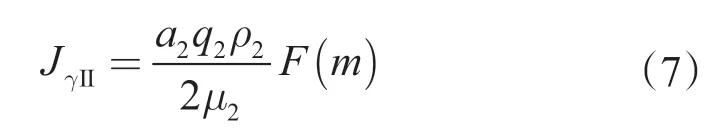
根据式（5）和式（7）可得：

（2）当在地层边界附近时，有：

当m ≥0 时，

当m=0 时，

当m ≤0 时，

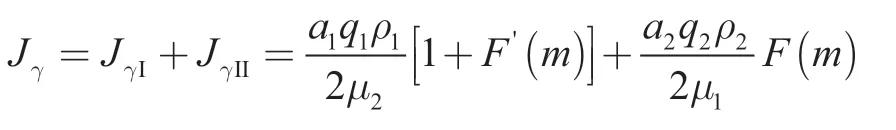
3 仿真与分析

图2 是根据上述模型利用matlab 进行模拟地层伽马探测的结果，计算探测点从Ⅰ区地层进入Ⅱ区地层，然后再进入其中地层Ⅰ，其中假设各项地层参数均为已知，并保证Ⅱ区地层厚度足够大，即保证伽马探测值仅受相邻两地层影响；如果需要考虑较薄地层，只须将上面推导中相关m 的值变动即可，在程序实现上也具有很好的可移植性。

图2 无限均匀水平地层中自然伽马通量matlab 模拟

从图中可以看出，在地层边界附近，伽马值都有比较明显的变化，并且在不同地层其变化的速率也不同，能够很好地区分出地层边界。

4 结论

（1）根据自然伽马在地层中的强度分布原理，推导出无限均匀水平地层中探测点距离边界的数学模型并给出了解析解。

（2）根据该模型可以很好地描述无限均匀水平地层中的自然伽马强度分布情况，能够识别探测点与地层边界的距离，对地质导向等技术具有一定参考价值。

（3）模型给出的解析解形式十分简单，便于编程计算分析提高效率，并且可以单独开发成计算模块供其它程序调用。

（4）该模型还有较大的完善空间，比如方位性、薄地层的识别等，还有待进一步分析研究以便尽快在实践中得以应用。

［1］ LEE W J, HOLDITCH SA F. Fracture evaluation with pressure transient testing in low-permeability gas reservoir［J］. Journal of Petroleum Technology, 1981, 9（6）∶ 1762-1776.

［2］ TURGAY Eetekin. Dynamic gas slippage-a unique pualmechanism approach to the flow gas slippage in tight formation［R］. SPE 12045.

［3］ 张桂林.胜利油田水平井钻井技术现状与发展趋势［J］.石油钻探技术，2005， 33（2）：66-70.

［4］ 孙清德.中国石化集团钻井技术现状及展望［J］.石油钻探技术，2006， 34（2）：1-6.

［5］ 狄富春，吕建云，赵立文，等.提高薄油层水平油层钻遇率的技术研究［J］.石油钻探技术，2008， 36（2）：25-27.

［6］ 庞巨丰.核测井物理基础［M］.北京：石油工业出版社， 2005：79-80.

［7］ 吴官生.地质导向法用于钻头前方地质情况预测［J］.石油物探译丛，1998，12（6）：76-82.