垂直裂缝气井不稳定产能预测新模型

李勇明 李亚洲 赵金洲 张烈辉

（油气藏地质及开发工程国家重点实验室·西南石油大学，四川成都 610500）

压后气井的动态产能预测对气井压裂设计和经济评价都有重要影响，因此，国内外对于压后气井产能的计算进行了大量的研究。黎洪等［1］利用二项式渗流规律推导出了高压气井产能的计算方法，但该方法只能用于高压气井，而且倾向于计算无阻流量，实际应用时有一定的局限性；李文学等［2］考虑了束缚水的影响，对产能方程进行了修改，实质是原产能方程的延续，只是多考虑了一个影响因子；蒋廷学等［3］利用保角变换推导了计算产能的简易公式，只用于计算稳态产能，不能预测整个生产过程；杨正明等［4］运用数值模拟对压裂井稳态产能进行了计算，但现场应用方面比较复杂。另外，还有一些关于压裂后气井产能的计算方法［5-9］，这些方法主要是根据现场测试资料和气藏地质情况，用气藏数值模拟的方法进行研究。这些方式对于现场实际应用来说不仅成本较高，而且操作过程复杂，不能很好地应用于现场生产。笔者根据垂直气井压裂后的裂缝形态及气体在裂缝和地层中的流动规律建立了垂直裂缝井不稳定渗流模型，推导出了垂直裂缝井的产能预测公式，并编写了软件。它能够对压裂气井产能进行快速计算，同时利用实例计算分析了地层参数和裂缝参数对垂直裂缝井产能的影响情况。

1 模型建立

根据垂直裂缝气井的形态和物理模型（图1）做如下假设：

（1）均质、水平、等厚且各向同性的封闭圆形边界气层，渗透率和孔隙度均不随压力的变化而变化，且为不稳定渗流；

（2）气体在气藏和裂缝内的流动为单相流，流动过程为先沿裂缝壁面均匀流入裂缝，再经裂缝流入井筒，并且二者均满足达西渗流定律；

（3）忽略了毛细管力、重力及温度变化的影响；

（4）裂缝完全穿透产层，裂缝的高度就等于产层的厚度，裂缝的两翼垂直于井筒且关于井筒对称。

图1 垂直裂缝井物理模型

2 气藏—裂缝—井筒渗流过程分析

2.1 地层任一点压降计算

地层中任意一点压降的计算是以封闭圆形边界的点汇定流量的压降公式［9］为基础。如将时间间隔取得很小，可近似认为在该段时间内流量为定值。

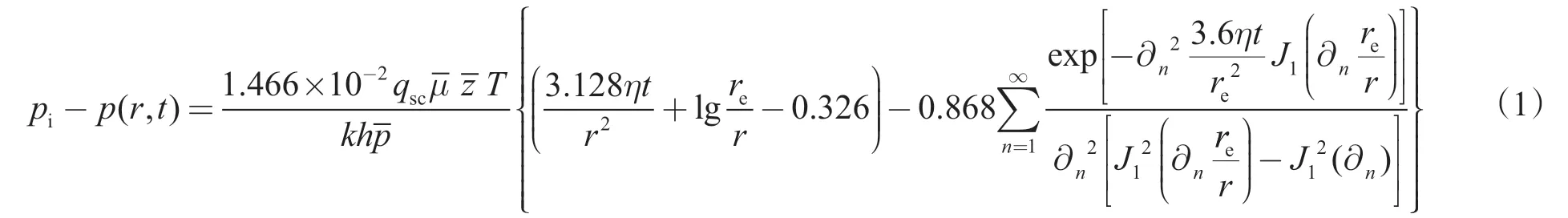
在考虑体积系数的情况下把式（1）转换为直角坐标形式，并利用贝塞尔函数的性质可以得到下式

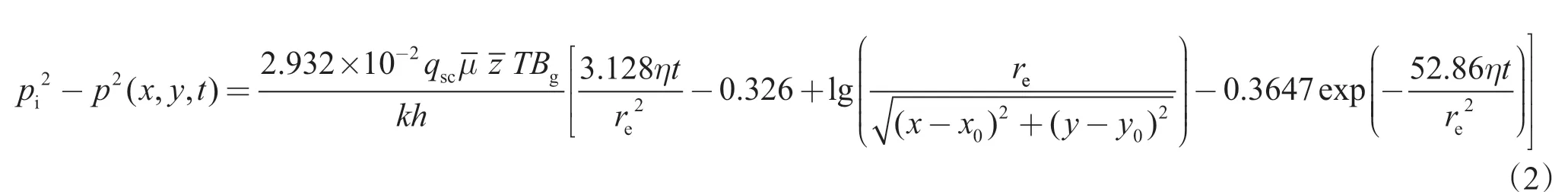
以垂直于裂缝平面的井轴的方向为y 轴方向，则裂缝可以看成是由无数个点汇所构成的直线汇。按照图2 所示，将裂缝两翼分别分成n 等份，每等份均作为点汇处理。

图2 裂缝等分示意图

此时，裂缝左右两翼上第j 个点汇的坐标（用第j 小段的中心坐标来表示）分别为

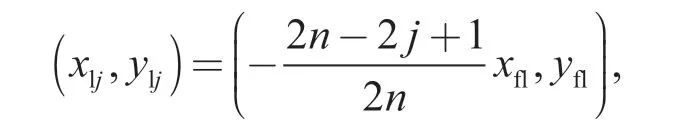
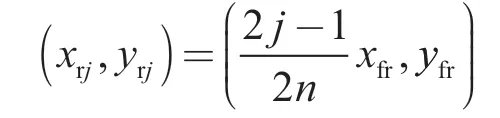
设左翼裂缝上第j 个点汇的产量为qflj，右翼裂缝上第j 个点汇的产量为qfrj。整条裂缝的产量为qf，所以有下式成立

将裂缝左、右翼上第j 个点汇各相应的参数分别带入式（2），可以得出裂缝左、右两翼上第j 个点汇对地层中任意一点（x，y）产生的压降。根据势的叠加原理，将左、右两翼上所有点汇对地层中任意一点（x，y）产生的压降相叠加，可以得出整条裂缝在t 时刻对地层中任意一点（x，y）产生的压降。

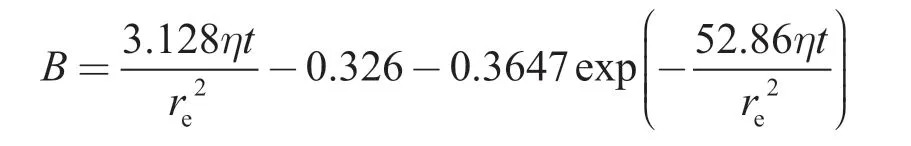
裂缝左翼尖端的坐标为

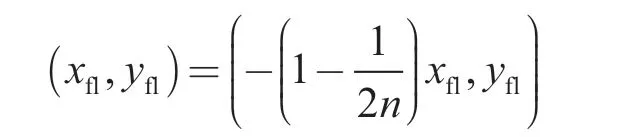
裂缝右尖端的坐标为

将裂缝左翼、右翼尖端的坐标值代入式（5）即可得到裂缝左右尖端的压降。

2.2 裂缝—井筒渗流方程

因为气体在裂缝中呈线性流，利用气体的状态方程、线性渗流的运动方程及达西渗流定律可以得到裂缝中气体的渗流方程［10］

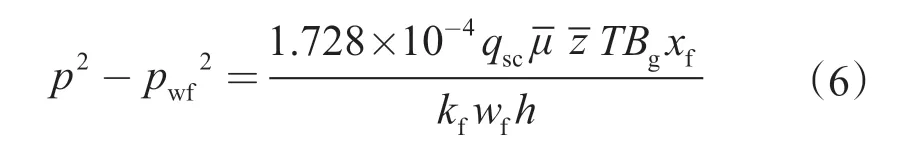
3 产能预测公式及求解

通过上一节对气藏—裂缝—井筒渗流过程的讨论分析可知，整个流动过程可以用下式进行表述

式（7）即为垂直裂缝井的产能预测公式。按照建好的坐标系中已经分隔好的裂缝微元段，用VB编制计算软件。先分别计算第j 个微元段的产量，最后把各个微元段（1～n）的产量求和即可得整条裂缝的产量qf。模型预测步骤见图3。

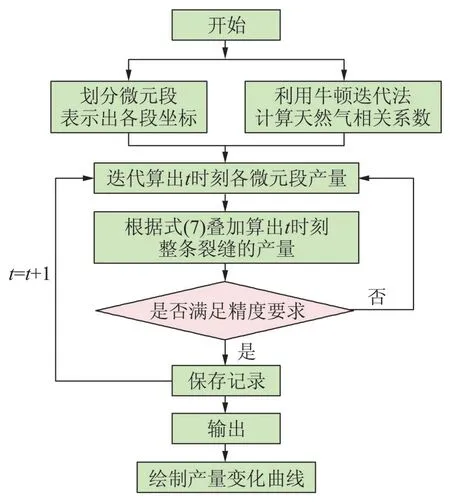
图3 产能预测计算框图

4 应用实例分析

应用本文建立的模型对吉林油田某垂直裂缝气井进行产能模拟计算，将计算结果和实际生产数据进行对比分析，并把各参数对产量的影响状况进行说明。

吉林油田某垂直裂缝气井基本参数：气藏厚度9.144 m，地层压力28.889 MPa，地层渗透率0.001 5 D，井筒半径0.076 2 m，井底流压23.548 MPa，体积系数0.02，裂缝半翼长度100 m，裂缝宽度0.005 m，裂缝渗透率60 D，生产时间365 d，孔隙度10%，边界半径500 m，地层温度395.6 K，天然气相对密度0.58。采用本文预测公式计算结果见图4。

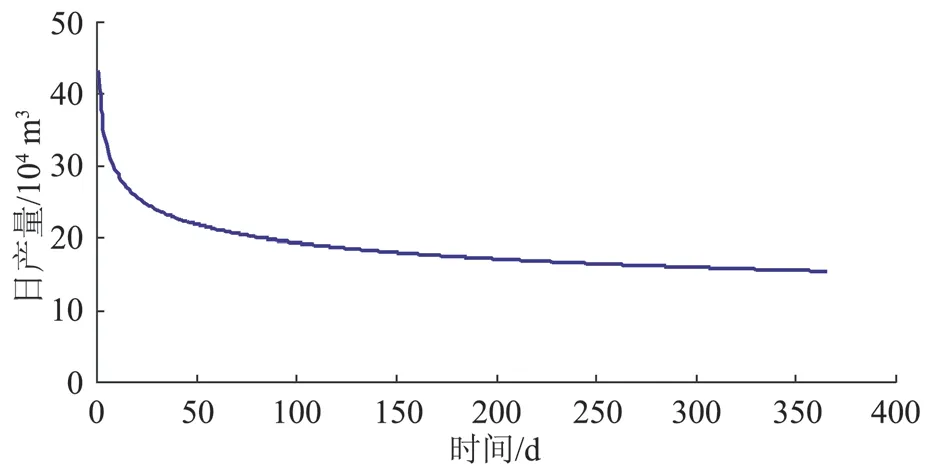
图4 产量随时间的变化关系

从图4 可以看出，在生产前期产量下降较快，后期产量下降速率趋于平稳，这种变化规律符合现场生产实际。根据现场资料，实际生产时年平均日产量为24.376 4×104m3/d，预测产量为25.234 4×104m3/d，实际产量和预测产量的误差为3.4%。实际产量和模拟产量存在一定差别主要是模拟计算受到提供的裂缝长度、裂缝渗透率和裂缝宽度等参数的影响。另外，实际生产时，裂缝或井筒可能存在污染现象，裂缝的渗透率也会随着生产时间的延续而发生变化，裂缝内存在一定的渗流阻力，这些现象的存在都会对产量产生一定的影响。

5 各参数影响状况分析

根据本文模型，改变输入参数后进行产量计算，得到不同参数下日产量随生产时间的变化数据（图5～9），从而模拟分析各裂缝参数和地层参数对垂直裂缝气井产量的影响状况。

图5 缝宽对垂直裂缝井产能的影响

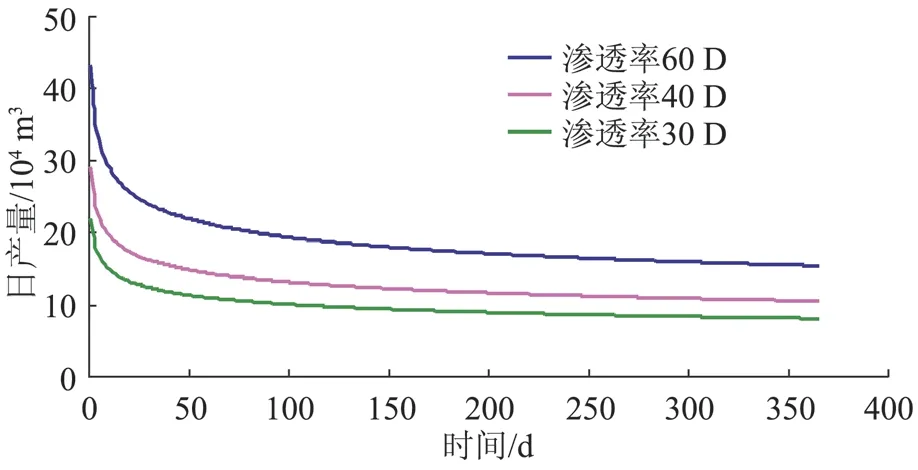
图6 裂缝渗透率对垂直裂缝井产能的影响

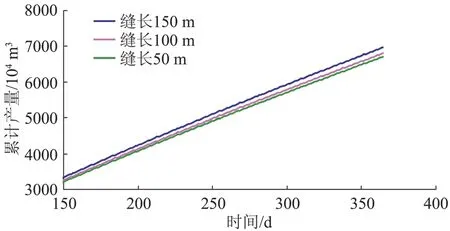
图7 缝长对垂直裂缝井产能的影响

图8 地层渗透率对垂直裂缝井产能的影响

图9 压差对垂直裂缝井产能的影响

由图5～9 可以看出，地层参数、裂缝参数、生产参数对压裂垂直井的产能都会产生一定的影响，但各参数的影响程度各不相同。从整体上来看，垂直裂缝井的产量随着裂缝导流能力、裂缝长度、地层渗透率、生产压差的增加而增加。其中对生产压差和裂缝导流能力的敏感性较强。因此，在进行压裂方案设计和实际施工时应抓住主要因素，使各个参数数值的大小控制在合理的范围内。

6 结论

（1） 利用渗流理论建立了封闭圆形均质地层垂直裂缝气井的渗流数学模型，并用渗流力学方法推导出了垂直裂缝井不稳定渗流的产量预测表达式。对吉林油田某垂直裂缝气井进行了例证分析，计算值和实际值的误差为3.4%，表明该预测公式准确性较高，能够满足现场要求。

（2） 通过得出的气井产量预测公式能够很好地分析地层渗透率、地层压力、气藏厚度等地层参数及裂缝长度、裂缝导流能力等裂缝参数对垂直裂缝气井产能的影响，为压裂设计及施工提供指导。

符号说明：

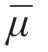
［1］ 黎洪，彭苏萍.高压气井产能评价方法研究［J］. 石油勘探与开发，2001，28（6）：77-79.

［2］ 李文学，马新仿，王玉敏.束缚水饱和度对水力压裂非达西气井产能的影响［J］.石油钻采工艺，2011，33（3）：35-37.

［3］ 蒋廷学，单文文，杨艳丽.垂直裂缝井稳态产能的计算［J］.石油勘探与开发，2001， 28（2）：53-56.

［4］ 杨正明，张松，张训华.气井压后稳态产能公式和压裂数值模拟研究［J］.天然气工业，2003，23（4）：74-76.

［5］ 董长银，饶鹏，冯胜利，等.高压砾石充填防砂气井产能预测与评价［J］. 石油钻采工艺，2005，27（3）：54-57.

［6］ 李勇明，郭建春，赵金洲.压裂气井模拟产能研究［J］.钻采工艺，2002，25（2）：40-42.

［7］ 董长银，李志芬，张琪，等.防砂井产能评价及预测方法［J］.石油钻采工艺，2002，24（6）：45-48.

［8］ 刘宇.复杂条件下垂直裂缝井压力动态及产能研究［D］.大庆：大庆石油学院，2006.

［9］ 蒋廷学，李安启，姜东.考虑井筒流动的垂直裂缝井稳态产能计算模型［J］.石油钻采工艺，2001，23（4）：50-53.

［10］ 李晓平.地下油气渗流力学［M］.北京：石油工业出版社，2007：125-126.