凸二次规划基于新的核函数的大步校正原始-对偶内点算法
汪 燕 张明望
(三峡大学理学院,湖北宜昌 443002)
本文根据原始-对偶内点算法的思想,基于Zhang M W 提出的一个新核函数[1],对凸二次规划设计了新的大步校正原始-对偶内点算法.考虑下面的凸二次规划及其对偶问题:

其中,x,c,s∈Rn,b,y∈Rm,Q∈Sn+,A∈Rm×n且rank(A)=m.
1 预备知识
1.1 中心路径
如果(x,y,s)是(P)和(D)的可行解,由对偶理论知,(x,y,s)是(P)和(D)的最优解的充要条件是

其中,xs=(x1s1,x2s2,…,xnsn)T,第3 个方程称为(P)和(D)的互补性条件.
根据原始-对偶内点算法的基本思想,用参数方程xs=μe(μ>0)代替方程组(1)中的第3个方程,即得如下方程组:

不失一般性,假设问题(P)和(D)满足内点条件(IPC),即存在内点(x0,y0,s0),满足

这时,对任意的μ>0,方程组(2)都有唯一解,记为(x(μ),y(μ),s(μ)).集合{(x(μ),y(μ),s(μ))}形成了一个同伦路径,称之为(P)和(D)的中心路径.若μ→0,则中心路径的极限值存在,且满足互补性条件,故此极限值即为(P)和(D)的最优解.
1.2 迭代方向
将牛顿法运用到方程组(2),得方程组
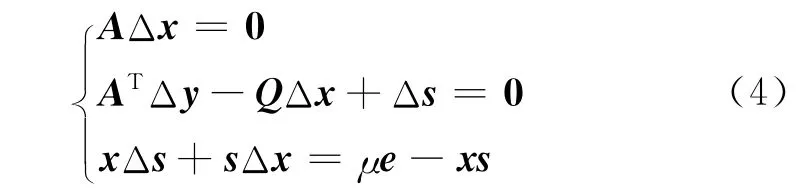
则方程组(4)的解(Δx,Δy,Δz)取作算法的迭代方向.
为了便于算法的分析,对任意的(x,s)>0,μ>0,定义:
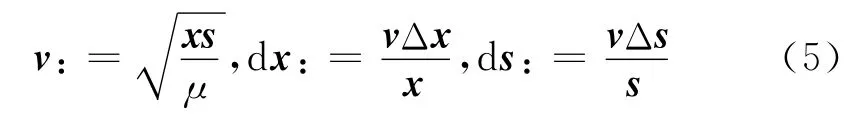
因此,方程组(4)等价于方程组


本文考虑的障碍函数Ψ(v)是开区间(0,+∞)上光滑的严格凸函数,且当v=e时取得最小值0,因此
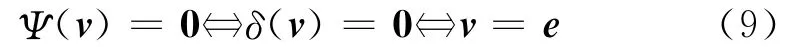
现在用-▽Ψ(v)替换(6)中的第3个方程的右半部分,得方程组

由于A 的秩为m 且满足(IPC),所以对任意μ>0,方程组(10)都有唯一解(dx,Δy,ds).再由(5),从而得到算法新的迭代方向(Δx,Δy,Δs).
若(x,y,s)≠(x(μ),y(μ),s(μ)),则(Δx,Δy,Δs)≠(0,0,0).迭代点(x,y,s)沿牛顿方向取步长α,有
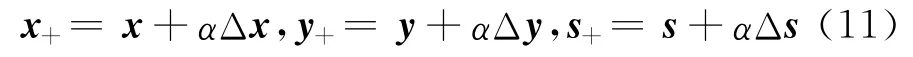
又因为Q 是半正定对称矩阵,所以有

这与线性规划中(dx)Tds=(ds)Tdx=0不同,这正是本文新算法与线性规划相应算法及其分析的主要不同之处.
1.3 凸二次规划的大步校正原始-对偶内点算法
现在具体描述凸二次规划的原始-对偶内点算法:
Step1:输入参数τ>0,精度参数ε>0,以及一个固定的障碍校正参数θ(0<θ<1),选一组严格初始可行解(x0,y0,s0),使得Ψ(x0,s0,μ0)≤τ(这里μ0=(x)0Ts0/n),令x:=x0,y:=y0,s:=s0,μ:=μ0.
Step2:如果nμ<ε,停止.此时的(x,y,s)便是ε-最优解,否则修改μ=(1-θ)μ,转Step3.
Step3:Ψ(v)≤τ,返回Step2,否则进入Step4.
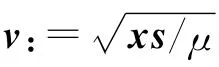
2 核函数的性质
本文引用文献[1]中的核函数

以下关于核函数的性质证明均类似于文献[1].
3 凸二次规划的算法分析
3.1 步长α的选择和障碍函数Ψ(v)的下降
设在内迭代过程中,当前点(x,s)经过一次内迭代之后,得到新的迭代点(x+,s+),其中


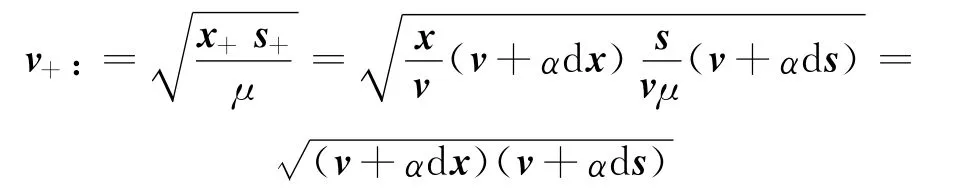
根据引理2.1,显然有f(α)≤f1(α),f(0)=f1(0)=0.
对f1(α)关于α求导可得

定义f(α):=Ψ(v+)-Ψ(v)和
于是
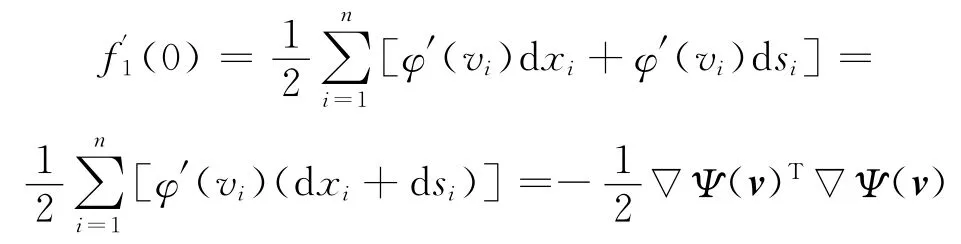
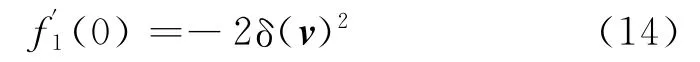
对f1(α)关于α求二阶导数可得

为方便讨论,记δ:=δ(v),vmin:=min{vi},i=1,…,n.
证明 根据δ(v)的定义,可得‖dx+ds‖=2δ,所以有‖dx‖≤2δ和‖ds‖≤2δ,由此可得

由于φ″(t)在(0,+∞)上单调递减,可得

所以
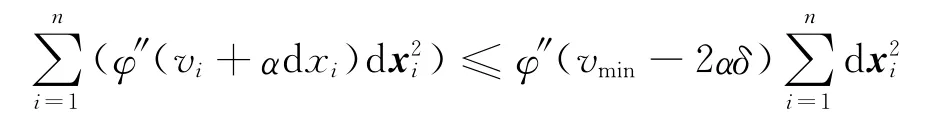
同理
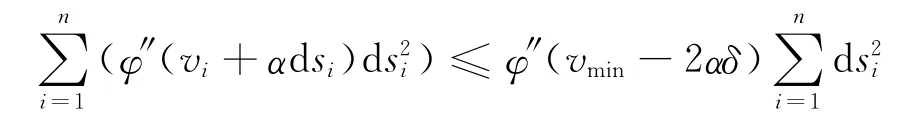
根据式(15),可得

证毕.
引理3.1.2 如果α满足不等式
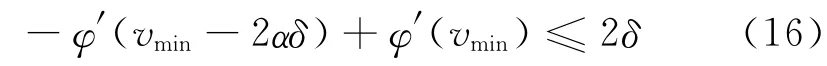
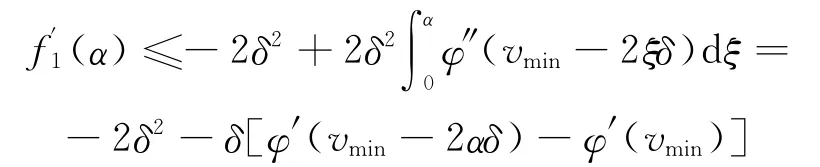
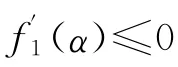

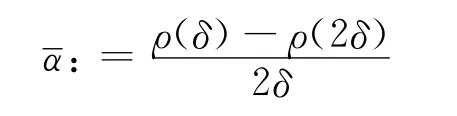

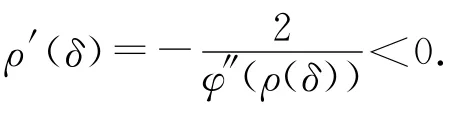


引理3.1.5(文献[3]中引理12) 若h(t)是一个二阶可微函数且满足h(0)=0,h′(0)<0,如果h(t)在t*>0处取得最小值,且h″(t)在[0,t*]上单调递增,则h″(t)≤h′(0)t/2,t∈[0,t*].

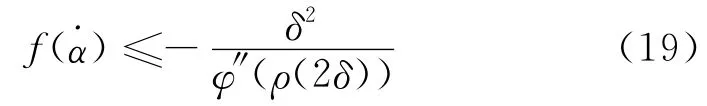
为讨论方便,记s=ρ(2δ),由ρ的定义,则有-φ′(s)=4δ.由核函数的一阶导数和二阶导数可得

所以

注意到0≤s≤1,则有
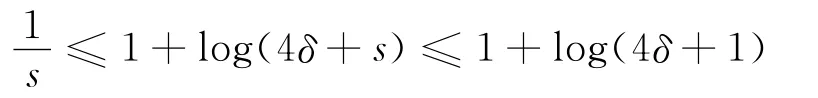
于是,有

从引理3.1.6,可得
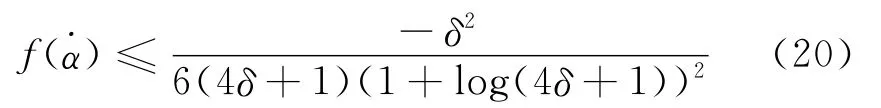
由于式(20)的右边不等式关于δ是单调递减的,利用引理2.3,可得

其中,这里的第二个不等式用到Ψ0≥Ψ≥τ≥1.
3.2 迭代复杂性分析
为了估计大步校正内点算法总的迭代复杂性,需要定量计算出算法在μ 修正以后,需要迭代多少步满足Ψ(v)≤τ.记μ 修正后Ψ(v)的值为Ψ0,此后的序列值记为Ψk,k=1,2,…,K.K 表示在一次外迭代中内迭代的总数目,则有

引理3.2.1(文献[3]中的引理14) 设t0,t1,…,tk是一列正实数,满足

引理3.2.2 设K 表示在一次外迭代之后内迭代的总数目,则有

证明 根据式(21),可得


证毕.
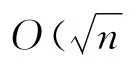
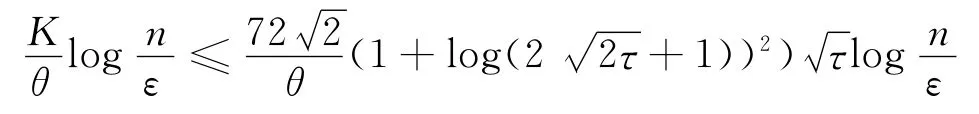

[1] Zhang M W.A Large-update Interior-point Algorithm for Convex Quadratic Semi-definite Optimization Based on a New Kernel Function[J].Acta Mathematica Sinica,English Series,2012,28(11):2313-2328.
[2] Bai Y Q,El Ghami M,Roos C.A Comparative Study of Kernel Functions for Primal-dual Interior-point Algorithms in Linear Optimization[J].SIAM Journal on Optimization,2004,15(1):101-128.
[3] Peng J,Roos C,Terlaky T.Self-regular Functions and New Search Directions for Linear and Semidefinite Optimization[J].Mathematical Programming,2002,93:129-171.

