考虑水封气的水驱气藏动态储量计算新方法

唐 川 赵家辉 张俊松 赵文娟 张 杰

1.西南石油大学，四川 成都 610500；

2.中国石化西南石油局井下作业公司，四川 德阳 618000；

3.中国石油四川泸州销售分公司，四川 泸州 646666；

4.中国石化西南石油局固井公司，四川 德阳 618000

0 前言

在非均质水驱气藏中，随着气田开发，天然气的不断采出使气藏压力下降，导致边水或底水侵入气区［1］。侵入气藏的水沿裂缝迅速上窜或横侵， 将部分气藏分隔开，然后继续向未被水封的区域运移，封隔气藏的更多区域［2-3］。若不进行强排水，水封气很难被采出，严重影响气藏的产量和采收率［4-6］。在研究水体活跃的水驱气藏动态储量时，首先关心的是水封气量，未被水封气量及水侵量，未被水封气量决定了气藏在未采取强排水时的采收率，水侵量决定了采出水封气量需排水的强度。

以往水驱气藏的物质平衡方程未考虑侵入水将气藏分割、包围的实际情况［7-8］，且无法确定被水封气量［9］。针对该问题，本文提出了一种新的物质平衡方程，考虑侵入水对气藏的分割与封闭，只需地层压力、累计采出气量、水量等数据，利用自动拟合方法直接计算水驱气藏各个时期的动态储量、未被水封气量、水封气量及水侵量，同时确定水驱强度指数。

1 水封气藏物质平衡方程

1.1 无水封的气藏物质平衡方程

对于水驱气藏，随着气藏压力下降，边水或底水将侵入气藏。 此时被水侵所占据的气藏孔隙体积量加上剩余天然气所占据的气藏孔隙体积量等于气藏的原始含气孔隙体积量，即有：

式中：Wc、Wp为累积天然水侵量和累积采出水量，108m3；Bw为地层水的体积系数；Bgi、Bg为原始条件下和目前压力下气体的体积系数； G、Gp为原始地质储量和目前累积采出气量，108m3。

1.2 考虑水封的气藏物质平衡方程

对于非均质水驱气藏，随着气藏的开发，水体侵入气藏，并沿裂缝上窜或横侵，将原气藏封隔为未被水封区域和水封区域，随着气藏的进一步开采，更多的水侵入气藏，并沿裂缝继续上窜或横侵，封闭更多气藏空间，使得未被水封气量进一步减少， 水封气量进一步增加，见图1。水封区域可能是多个不连续的区域，未被水封气量和水封气量分别为G1和G2，侵入水量为We1。

图1 水封气藏物质平衡

假定某一时期气藏被水分割为n 个独立区域，每个区域的水封气量分别为G21、G22…G2i…G2n，封隔各区域的水体分别为We21、We22…We2i…We2n，见图2。生产时未被水封区压力降低，水封区气体膨胀进入未被水封区，膨胀的体积分别为V21、V22…V2i…V2n。

图2 水封气藏各区域物质平衡

考虑水封区各独立区域的物质平衡：

即：

未被水封区的物质平衡为：

可以看到， 在不同时期水侵量We1、We2， 气量G1、G2均是变化的，但在气井正常生产无强排水工艺时期，基本的变化趋势为气量G1不断减小、气量G2不断增大，水体We2不断增大，直至气井被水淹。

将式（3）、（4）联立，得到水封气藏物质平衡方程：

由于水侵量We均符合水侵体积系数ω 与采出程度R 的函数关系，采用常规方法计算：

由式（6）得：

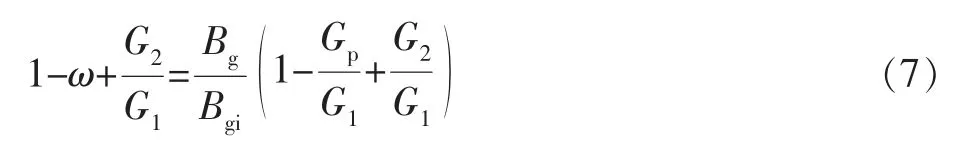
即：

式中：φ 为视相对压力； A 为未被水封气量G1的倒数；B 为We1的水侵强度；C 为被水封闭的储量G2。

2 水封气藏物质平衡自动拟合方法

自动拟合算法的实质是参数识别问题，即寻求最优参数理论值与实测值的最佳拟合，使误差为最小，表示为：

式中：φ实测为测得生产过程中的视压力；φ理论为由式（9）计算的理论值；E 为目标函数。

式（10）为非线性最小二乘问题，采用自动拟合方法进行拟合，寻求一组合理参数使目标函数E 达到最小。

3 实例分析

四川盆地x1 气井于1979 年4 月投产，1985 年9 月见水，1990 年3 月采取关井复压、 间歇泡排工艺生产，至今累积采出气量1.67×108m3， 累积采出水量7.2×104m3。根据压降法计算动态储量为5.8×108m3，生产数据见图3。

经新方法自动拟合计算， 新方法视相对压力拟合曲线和实际视相对压力曲线的对比见图4，视相对压力拟合效果较好。新方法计算储量与压降法计算储量一致，其结果见表1。 新方法计算水侵强度与水驱气藏曲线拟合法计算水侵强度一致，见图5。综上说明新方法计算结果正确、可靠。

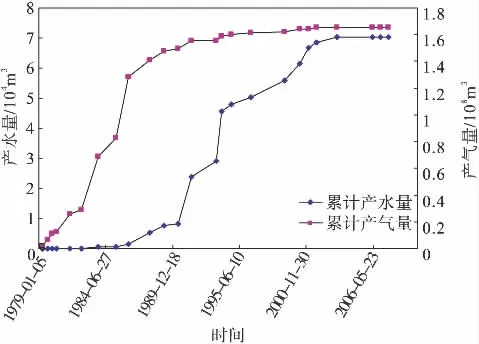
图3 x1 井累积产气和累积产水曲线

图4 新方法视相对压力拟合对比图

表1 新方法计算结果

由新方法计算出了x1 井各时期未被水封气量、水封气量、水侵量等数据，见图6。 1985 年6 月～1987 年3 月，水封气量迅速增加，未被水封气量急速减小，之后两者维持相对稳定。 判断该井大面积水封就发生在这一时期，与该气井1985 年9 月见水的事实吻合。

图5 水驱气藏曲线拟合法图版

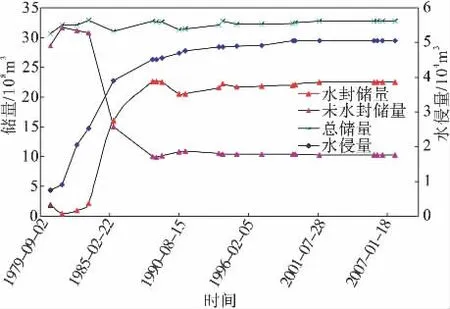
图6 X1 井各时期水侵量与动态储量

将新方法与未考虑水封气作用的水驱气藏曲线拟合法比较， 把实际视相对压力值放入曲线拟合法图版内，发现见水后实际值与图版曲线相差很大，无法通过图版曲线求得x1 井的水侵量、动态储量。

4 结论

a）根据水封性水驱气藏的特点，提出了该类气藏的物质平衡方程，利用自动拟合法计算气藏各时期水封气量与水侵量。

b）由新方法计算出了x1 井各时期的动态数据。 该井大面积水封发生在1985 年6 月～1987 年3 月间，这与该气井1985 年9 月见水的事实吻合。

c）将新方法计算结果与压降法、水驱气藏曲线拟合法比较，发现新方法计算出的动态储量较为可靠，同时获得了水封气动态参数。

［1］ 李士伦.天然气工程［M］.北京：石油工业出版社，2000.79-81.

［2］ 刘国霖，孔玉明，沈 蔚，等. 低渗透储层水锁伤害解除技术室内研究［J］. 天然气与石油，2012，30（4）：67-69.

［3］ 卜彩霞，林丽娜，王永恒. 积液倒灌和水锁效应对气井生产的危害［J］. 天然气与石油，2011，29（5）：53-56.

［4］ 孙良田. 油层物理实验［M］. 北京：石油工业出版社，1992.79-81

［5］ 疏壮志，杜志敏，刘建仪，等. 碳酸盐岩裂缝性水驱气藏水锁实验研究［J］. 天然气工业，2004，24（6）：89-92.

［6］ 罗 涛，王 阳. 裂缝水窜气藏单井数值模拟研究［J］. 天然气工业，2002，22（增刊）：95-97.

［7］ 王怒涛，黄炳光，张崇军，等. 水驱气藏动态储量及水侵量计算新方法［J］. 西南石油学院学报，2000，22（4）：61-67.

［8］ 杨继盛. 采气工艺基础［M］. 北京：石油工业出版社，1992.

［9］John L.Gas Reservoir Engineering［M］.New York：Society of Petroleum Engineers，1996.121-127.