基于动柔度法的二元机翼颤振主动控制试验研究*

王囡囡，侯友夫

(中国矿业大学 机电工程学院，江苏 徐州 221116)

0 引言

颤振是最重要、也是最难以预测的气动不稳定现象，主要涉及到气动力、结构弹性力和惯性力等的相互作用［1-3］。颤振发生时机翼从气流中汲取能量从而导致结构发生灾难性破坏，因此必须采取一定的措施抑制颤振现象的发生，其中颤振主动振动控制技术是近年来研究的热点［4-5］。颤动主动控制利用极点配置理论，通过控制反馈改变原开环系统的极点分布，使系统具有期望的闭环极点，达到闭环稳定［6］。随着现代飞机设计过程中对操纵性、稳定性、高速性以及舒适性等性能要求的提高，控制系统必须具有良好的鲁棒性，且易于实现。

基于动柔度法的颤振主动控制技术是控制领域的一个创新点［7-8］，该技术的最大优点是基于试验获得的系统的频率响应函数，因此无需事先确定系统的质量、刚度和阻尼特性，根据实际系统的动态特性，配合一定的反馈控制律即可实现闭环系统的稳定性。

本文以NACA0018 型二元机翼为试验对象，首先建立机翼系统的动柔度模型，然后根据极点配置理论求解系统的反馈控制增益，最后对机翼进行试验，验证动柔度法在极点配置中的应用。

1 二元机翼系统动柔度模型

具有沉浮和俯仰两自由度的机翼模型如图1 所示，基于准定常气动力理论建立气动弹性方程为［9］:

其中，A，B，C，D，E 分别为结构惯性、气动阻尼、气动刚度、结构阻尼和结构刚度矩阵，q(t)为广义模态坐标，p(t)为控制力，各个参数的具体表达式详见文献。

图1 二元机翼模型

将式(1)经过拉氏变换后得到开环系统的动柔度，即系统的频率响应函数为:

当系统采用闭环控制时，机翼的控制力由操纵面的转动提供，系统采用PD 控制律，因此控制力为:

其中，非零向量f 和g 分别为控制器提供的速度和位移反馈增益系数。

将式(3)代入式(1)并经过拉氏变换后，根据Sherman-Morrison 定理［10］得到闭环系统的动柔度为:

2 二元机翼颤振主动控制试验系统设计

根据动柔度法的理论可知，机翼系统的频率响应函数可通过模态试验得到。因此，首先测试机翼系统在不同风速下的开环频率响应函数;然后基于开环频率响应函数，利用极点配置理论计算得到闭环系统的反馈控制增益系数，并测试闭环系统的动态特性;最后测试机翼系统的临界颤振速度，验证通过闭环控制可以提高机翼的颤振速度。

2.1 试验系统组成

机翼振动主动控制的整个试验系统组成如图2所示，主要包括风洞试验台、机翼模型、作动器、传感器、功率放大器、控制系统和LMS 数据处理系统;机翼系统的试验装置如图3 所示。

图2 机翼主动控制试验系统

图3 试验系统装置

(1)风洞试验台:根据运动的相似性原理，将试验对象安置在风洞管道内，通过驱动装置产生一种人工可控的气流，模拟试验对象在不同气流作用下的动态性能，获得相关参数。

(2)机翼模型:采用NACA0018 型机翼模型，其截面骨架如图4 所示，弦长为0.35m，展长为1.2m。机翼采用木质结构，具有重量轻、造价低、易于控制等优点。由主翼面、控制面和附属安装机构组成。机翼通过刚度可调的垂直和扭转钢板弹簧安装在风洞试验台上，实现沉浮运动和俯仰运动。

图4 机翼截面模型

实现机翼沉浮运动的试验装置如图5 所示，钢板弹簧一端与机翼通过轴承与机翼连接，另一端通过夹具与风洞试验台固定连接。由于钢板弹簧上加工有不同的安装孔，因此根据图中箭头方向调节夹具与钢板弹簧的安装位置即可实现改变垂直弹簧刚度kh，其中弹簧刚度随位移的变化曲线如图6 所示。

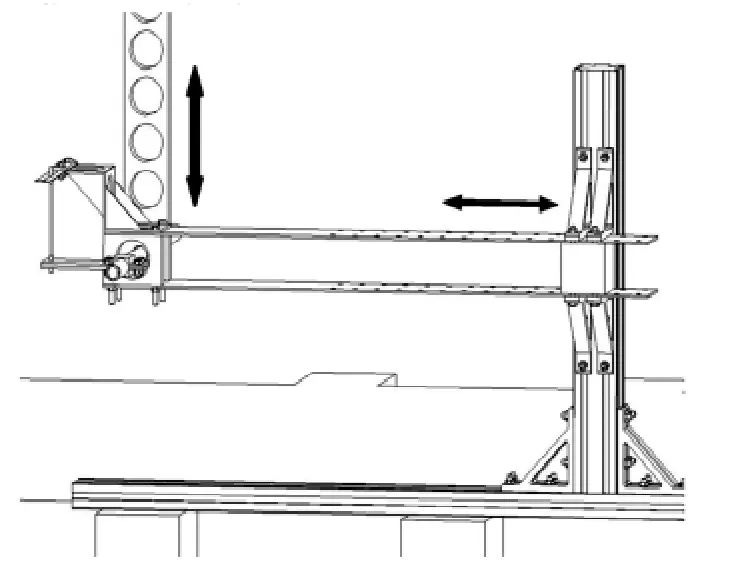
图5 可调的垂直弹簧

图6 垂直弹簧刚度

实现机翼俯仰运动的试验装置如图7 所示，俯仰刚度由图中的钢板弹簧提供，一端通过夹具固定在风洞试验台上，另一端通过轴与机翼连接。同样，由于钢板弹簧上加工有多个安装孔，根据图中箭头所示的方向调节夹具的位置使机翼系统获得不同的扭转刚度kθ，其中扭转刚度随位移的变化曲线如图8所示。

图7 可调的扭转弹簧

图8 扭转弹簧刚度

根据垂直弹簧刚度和扭转弹簧刚度可以计算得到机翼气弹系统的颤振速度范围大约为10 ～40m/s。由于颤振是一种非常危险的工况，所以应在保证系统安全的前提下选择合适的风洞速度。

(3)传感器:试验采用基恩士公司8636C50 型加速度传感器，测量机翼的沉浮、俯仰和控制面的偏转三个自由度的运动。

(4)作动器:试验采用一种新型的V 型叠加式压电作动器，如图9 所示。该类型的作动器具有位移分辨率高、线性度好、体积小、重量轻且没有电磁污染和油污染等优点。由于作动器内置在机翼模型中，因此，为减小作动器本身的动态性能对机翼系统的影响，其固有频率应远远大于机翼系统的固有频率。作动器允许的襟翼偏转角为±7°，扑动频率范围为25 ～30Hz。

(5)功率放大器:试验采用Krohn-Hite 7500 型宽带功率放大器，具有高阻抗、扩展带宽、直流和输入输出电压信号稳定高，热稳定性好等优点。

(6)控制系统:作为机翼振动主动控制试验系统的核心部分，实现系统的开环和闭环控制。控制系统主要包括各个硬件参数设置、控制律计算、数据分析处理、控制测量信号的输入与输出以及对测量数据的实时动态显示与调试等功能，控制系统的流程图如图10 所示。

图9 作动器

图10 控制系统流程图

(7)LMS 数据处理系统:数据处理系统与控制系统是相互作用的，通过动态数据采集系统对所测试验数据进行计算处理，同时将结果反馈到系统中。本试验采用LMS SCADAS Ⅲ数据采集器对信号进行调理和数据采集任务，它是基于快速傅里叶变换原理和数字信号处理技术，对输入的传感器信号通过抗混滤波、采样和模块转换等初步处理后进行数据的存盘记录，同时根据不同要求对信号进行实时与事后的时域分析、频域分析、相关分析以及幅值域分析等，还可以联合MATLAB 工具箱的数据处理模块对试验结果进行进一步地分析处理。

3 动柔度法的应用

系统的动柔度即为系统的频率响应函数(FRFs)。本试验采用相位分离法得到机翼系统的频率响应函数，主要步骤如下:

(1)在感兴趣的频率范围内激励机翼并测量输入输出响应;

在本试验中机翼系统的感兴趣频率范围为0.5～30Hz，频率分辨率为0.05Hz。作动器的激励信号经过功率放大器的输入电压为vβ，加速度传感器测量得到的沉浮和俯仰加速度经过积分后的位移分别为x1和x2，当风速v 一定时，机翼系统的输入输出关系可表示为:

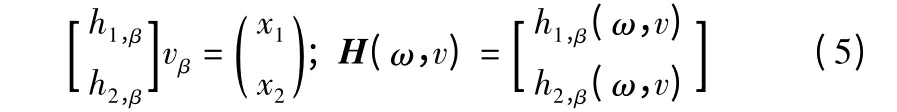
机翼系统的速度频率响应函数为:

在对机翼系统的频率响应函数进行分析时，应注意式(5)和(6)所表示的开环动柔度不仅包括了机翼系统本身的动力学特性，而且还包括了功率放大器、作动器、传感器以及A/D 和D/A 转换器的动态响应，在对加速度进行积分计算时还包括了数值计算误差以及低通和高通滤波器的截断频率误差等。

(2)对激励和响应信号在时域或频域内进行曲线拟合;

当得到系统的频率响应函数后，利用MATLAB 结构动力学工具箱中的Pole-Residue 模型对其进行多项式拟合，即可得到系统的传递函数H(s，v)和(s，v)。

(3)计算动柔度系数矩阵;点μ1，和μ2代入传递函数中得到机翼系统的

若实现系统的极点配置，将两对共轭的期望极系数矩阵为:

从动柔度法的实际应用可以看出，动柔度法的最大优点是无需预先确定系统的惯性、阻尼和刚度矩阵，无需对系统的结构或气动参数进行简化或假设，因此整个机翼系统的控制效果仅仅取决于试验测得的频率响应函数H(ω，v)和(ω，v)。

(4)计算反馈控制增益系数。

当机翼开环系统的动柔度H(s)和期望极点s 给定时，则根据式(4)的特征多项式

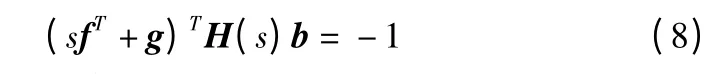
经过整理后可得

通过式(9)即可计算得到闭环系统的反馈控制增益系数。

4 风洞振动试验结果

为得到机翼的基本模态参数，对系统进行初步模态试验，利用激振锤对整个机翼试验系统进行激励，得到系统的频率响应函数如图11 所示，前两阶模态为机翼的沉浮和俯仰模态，频率值分别为3.9Hz和6.7Hz;机翼的一阶弯曲模态频率为41Hz，一阶扭转模态频率为47Hz，与机翼的弹性模态可以明显区分开;同时得到机翼附属支撑结构的模态频率在20～40Hz 范围内。

试验采用单输入单输出方法测试机翼的动态特性，作动器提供阶跃——正弦输入信号，加速度传感器测量系统的输出。图12 是风速在7m/s 时机翼开环系统的幅频和相频特性的试验曲线和拟合曲线。

从图12 可以看出，机翼的沉浮和俯仰两自由度的频率值。但是从试验频率响应特性可以发现试验结果比常规的振动模态试验结果波动更严重，引起波动的原因主要有以下几个因素:作动器和传感器本身的动态特性，控制面的转动引起的气动弹性影响以及测试过程中的噪声干扰等。

图11 整个机翼系统的频率响应

图12 机翼频率响应试验曲线和拟合曲线

当得到机翼开环系统的拟合频率响应函数后，根据基于动柔度法的极点配置理论即可计算闭环控制系统的反馈增益系数g 和f。为了使俯仰模态的阻尼比从1%增加为2%，而沉浮模态的阻尼比保持不变，所以根据机翼系统的开环极点－ 0.48 ±41.63i，设定相应的闭环期望配置极点为－0.9 ±41.63i。当风速为7m/s 时，计算得到反馈增益系数为g=77.103，f=－175.67;图13 给出了机翼在该风速下的开环和闭环频率响应曲线。

图13 机翼开环和闭环频率响应试验曲线

从图13 可以看出，对机翼系统施加控制后，俯仰模态的阻尼比明显增加，但是频率并未发生改变;而沉浮模态虽然阻尼比变化很小，但是频率向左“移动”，即由于俯仰阻尼比的变化使沉浮模态的频率有所改变。对比实测的机翼系统的频率响应曲线，可以看出基于动柔度法的极点配置理论在闭环控制中具有很好的鲁棒性。

机翼俯仰运动的位移响应如图14 所示。从图中可以看出，通过闭环控制可缩短响应衰减的时间，同时降低振动的幅值，从而提高系统的稳定性。

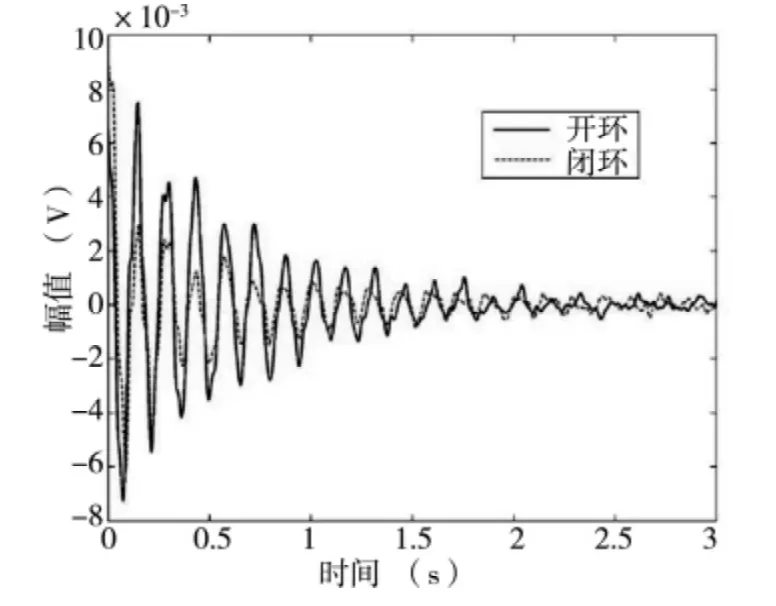
图14 机翼俯仰运动的时间响应曲线

5 结束语

本文以NACA0018 型二元机翼为试验对象，采用动柔度法实现了机翼系统的振动主动控制。通过风洞振动试验主要得到以下结论:①采用动柔度法时无需预先确定系统的质量、阻尼和刚度特征;②将动柔度应用到闭环极点配置时，系统具有良好的稳定性及鲁棒性;③通过极点配置可以实现系统的期望动态特性，如模态频率和阻尼比。

［1］陈桂彬，邹丛青，杨超. 气动弹性设计基础［M］. 北京:北京航空航天大学出版社，2004.

［2］宋晨，吴志刚，杨超. 二元机翼滑模变结构控制颤振主动抑制［J］. 北京航空航天大学学报，2010，36(12):1400－1404.

［3］贾文铜，周瑞祥. 基于模糊控制的飞机平尾舵机伺服系统动态仿真［J］. 组合机床与自动化加工技术，2011(3):45－48.

［4］Waszak M R，Srinathkumar S. Flutter suppression for the active flexible wing control design and experimental validation［C］AIAA，1992(2):138－145.

［5］Njuguna J. Flutter prediction，suppression and control in aircraft composite wings as a design prerequisite:A survey，Structural Control and Health Monitoring［C］2007(14):715－758.

［6］Mottershead J E，Tehrani M G，James S，Ram Y M. Active vibration suppression by pole－zero placement using measured recptances［J］. Journal of Sound and Vibration，2009，23(6):1931－1939.

［7］Tehrani M G，Mottershead J E，Shenton A T，Ram Y M.Robust pole placement in structures by the method of receptances［J］. Mechanical Systems and Signal Processing，2011，25(1):112－122.

［8］Ram Y M，Mottershead J E. Receptance method in active vibration control［J］. American Institute of Aernautics and Astronautics Journal. 2007，45(3):562－567.

［9］Jan，R W，Jonathan E C. Introduction to Aircraft Aeroelasticity and Loads［M］，John Wiley ＆ Sons，Ltd press，New York，2007.

［10］张贤达. 矩阵分析与应用［M］. 北京:清华大学出版社，2004.