基于超弹性模型的牙周膜生物力学响应

黄辉祥 汤文成 吴 斌 严 斌

(1东南大学机械工程学院, 南京 211189)

(2南京林业大学机电工程学院, 南京 210037)

(3南京医科大学口腔医学院, 南京 210029)

牙周膜是连接牙齿与牙槽骨之间的纤维结蒂组织,其具有支持牙齿,传递、吸收和分散咬合力的作用,在口腔正畸及其生物力学研究中扮演着重要的角色．正畸矫治中,正畸力通过牙齿作用在牙周组织上,进而直接或间接地作用在颌骨上,从而引起一系列的生物反应,致使牙槽骨发生改建,最终使牙齿的位置发生变化,产生移动．牙周膜的应力、应变是正畸牙齿移动的始动因素,参与牙槽骨的重建过程[1-2]．由于牙周膜的复杂性及实验力学的局限性,当前对牙周膜的生物力学研究多采用有限元方法．要获得准确的有限元分析结果,合适的牙周膜材料本构模型是关键,牙周膜的生物力学响应可以通过本构模型来进行预测,从而为牙齿动态仿真及正畸力量化奠定理论基础．以前的有限元分析中牙周膜多采用线弹性本构模型[3-4],但是牙周膜表现出明显的非线性,其生物力学特性也更适于用非线性本构模型来描述[5],其本构关系曲线具有指数形式,当前研究局限于采用经典常规的超弹性模型来研究牙周膜的力学性能,低阶模型描述能力差,高阶模型参数多且参数因牙周膜实验数据缺少而不易确定,因此,用尽可能少的参数描述牙周膜材料的实际力学性能且无显著偏差的超弹性模型是必要的．但利用指数形式的超弹性模型开展牙周膜生物力学响应的研究鲜有报道．本文基于指数形式的超弹性模型,借助于有限元模型子程序对正畸力下牙周膜的生物力学响应进行了分析研究．

1 超弹性本构模型

超弹性模型的本构关系可以用应变能的形式表示[6]:

(1)

(2)

(3)

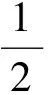
(4)

第二Piola-Kirchhoff应力张量为

(5)

则不可压缩材料的Cauchy应力为

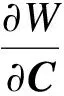
(6)

式中，p为静水压力.

超弹性本构模型较多,目前得到广泛应用的主要有Mooney-Rivlin模型、Neo-Hookean模型、Yeoh模型和Ogden模型等[2]．对于生物软组织来说,其应力-应变关系曲线表现为指数形式[7],即初始应力随应变平缓变化,当应变达到一定程度时,应力随应变迅速增加,而Mooney-Rivlin模型、Neo-Hookean模型及低阶Ogden模型等的指数性较差．为了能够更好地描述生物软组织的力学特性,一些学者在原有经典模型的基础上提出了指数形式的修正模型,主要有Mooney-Rivlin指数模型[8]、Ogden指数模型[7]等．

Mooney-Rivlin指数模型为

W=c1(exp(c2(I1-3))-1)+c3(I2-3)

(7)

式中,c1,c2,c3为材料参数．

由式(6)、(7)及单轴拉伸条件(σ22=σ33=0),可得

p=2λ-1[c1c2exp(c2(λ2+2λ-1-3))+c3(λ2+λ-1)]

(8)

σ11=2c1c2exp(c2(λ2+2λ-1-3))·
(λ2-λ-1)+2c3(λ-λ-2)

(9)

Ogden指数模型为

(10)

式中,α1,α2为材料参数．

(11)

σ11=2c1c2exp(c2(λα1+2λ-α1/2-3))·

(λα1-λ-α1/2)+2c3α2(λα2-λ-α2/2)

(12)

在实际工程应用中,通常可直接测量获得工程应力τ(即第一Piola-Kirchhoff应力)和工程应变ε.工程应力τ与Cauchy应力σ(真应力)的关系为

σ=τFT

(13)

利用伸长率与工程应变关系λi=1+εi(i=1,2,3),式(9)与式(12)可改写为拉伸方向上的工程应力τ与工程应变ε的关系．

2 本构模型参数确定

牙周膜本构模型研究在国内较少,缺少相关的实验数据,而在国外是研究热点,但由于人类牙周膜结构的复杂性和特殊性,较多的是采用动物实验.文献[9]数据来源于对2名女性患者的体内拉伸实验,虽然获得的数据较少,但可信度较高[5]．因此本文采用文献[9]中牙周膜的单轴拉伸实验数据分别对Ogden指数模型和Mooney-Rivlin指数模型以最小二乘法进行拟合,拟合曲线如图1所示,拟合计算获得的模型参数见表1．数据拟合的相对误差为

(14)

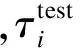
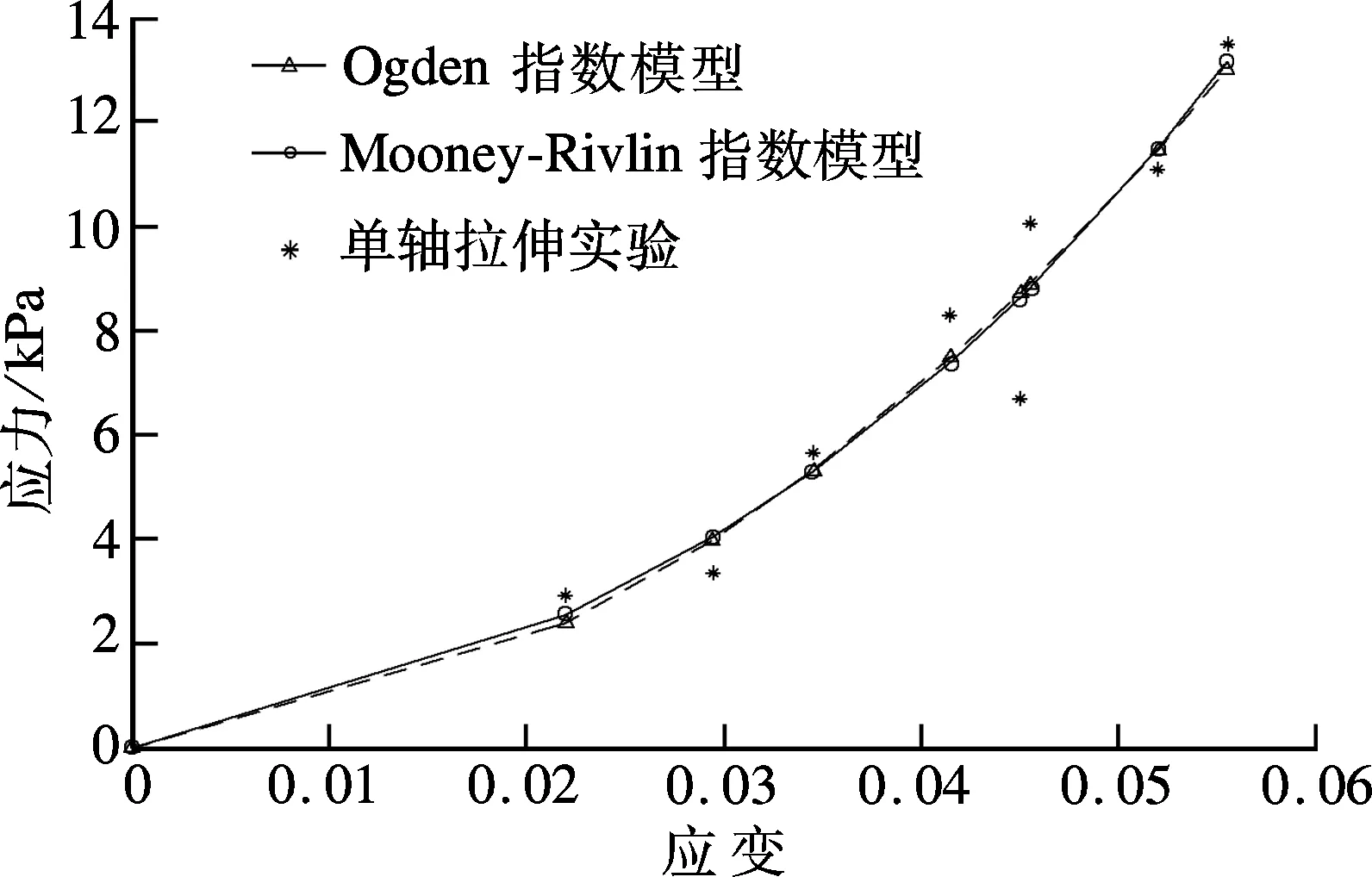
图1 Ogden与Mooney-Rivlin指数模型的拟合曲线

表1 超弹性指数模型参数

从图1可见,Ogden指数模型和Mooney-Rivlin指数模型与单轴拉伸实验数据的拟合效果较好,其数据拟合的相对误差分别为0.1639和0.1589．虽然两模型数据拟合的相对误差较大,但其拟合曲线在整个应变区域是稳定的,拟合误差较大可能是文献[9]中的牙周膜单轴拉伸实验数据的分散性大所致．从计算的拟合相对误差来说,Mooney-Rivlin指数模型更适合描述牙周膜的瞬时超弹性．

3 有限元模拟与分析

3.1 模型的有限元实现及验证

本文采用Mooney-Rivlin指数模型对牙周膜生物力学响应进行分析,由于通用有限元软件ABAQUS材料库中缺少Mooney-Rivlin指数材料本构模型,需要对其用户子程序UHYPER或UMAT进行二次开发．

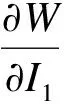
为验证Mooney-Rivlin指数模型UHYPER子程序的有效性,对牙周膜拉伸实验情况进行模拟计算,施加的拉伸载荷为1MPa,利用UHYPER子程序进行计算获得的应力分布云图如图2所示．选取其中一个单元,提取该单元一个积分点处的应力和应变值,得到应力-应变关系曲线(即数值仿真曲线),与理论模型曲线进行对比,如图3所示．从图3可看出,应用UHYPER子程序后ABAQUS计算结果与实验数据拟合结果具有良好的一致性,表明了本文开发的Mooney-Rivlin指数模型UHYPER子程序的正确性及有效性．

图2 牙周膜拉伸模拟应力云图

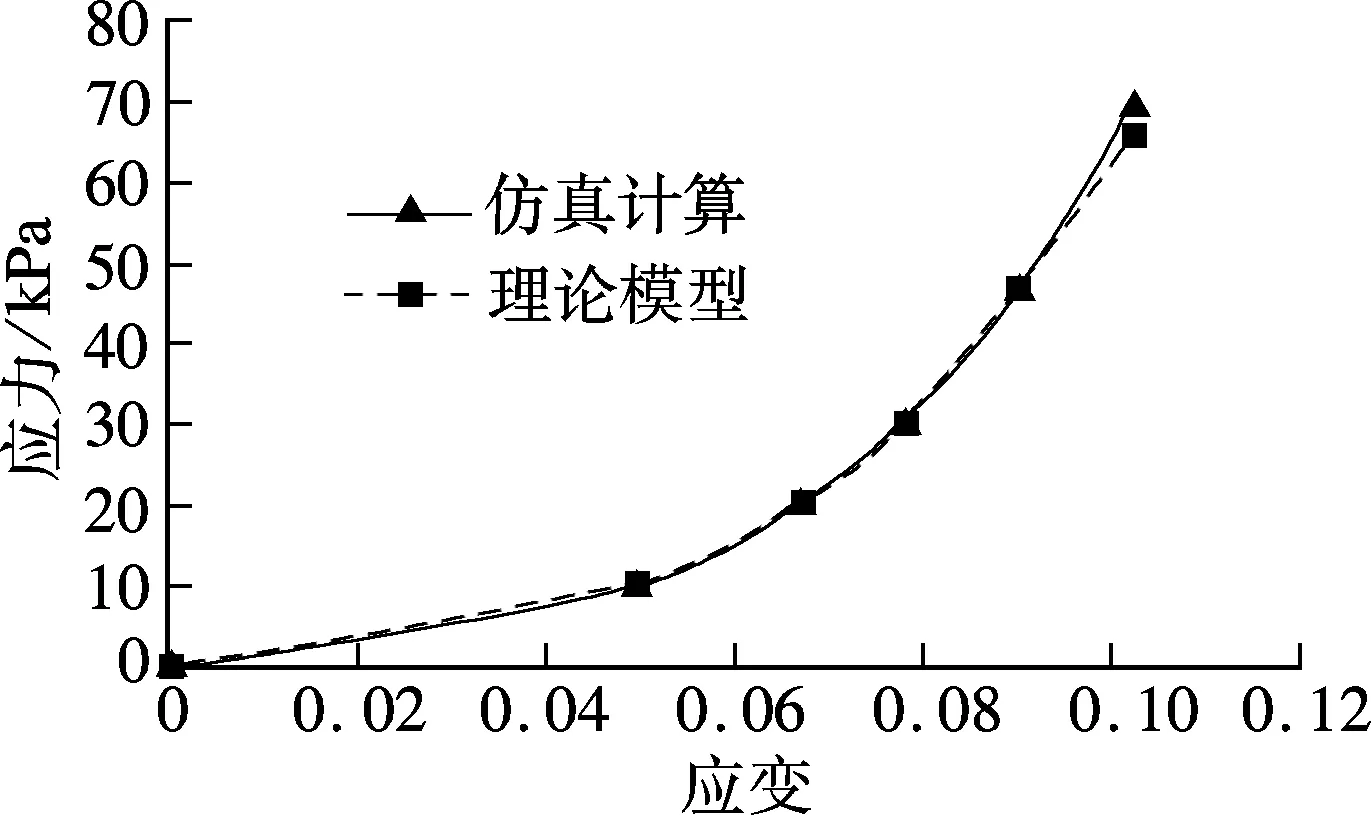
图3 应力-应变关系曲线对比

3.2 有限元建模及分析

采用CT对正畸患者的上中切牙进行扫描,借助于医学图像建模软件Mimics和逆向工程软件Catia建立牙齿、牙周膜和牙槽骨的三维几何模型,如图4所示,牙周膜厚度为0.2mm,位于牙齿和牙槽骨之间．由于牙齿和牙槽骨的弹性模量是牙周膜的20000～30000倍,因此在有限元模型中将牙齿和牙槽骨作为刚性体以节省计算资源,它们和牙周膜之间的接触约束采用绑定连接,牙周膜采用C3D8H单元,在牙冠上唇舌方向施加大小为1N的正畸力,利用开发超弹性模型的ABAQUS子程序UHYPER及线弹性模型分别对牙周膜在正畸力作用下的生物力学响应进行模拟分析研究．线弹性模型中设置牙周膜弹性模量为0.667MPa,泊松比为0.49[11]．

图4 中切牙、牙周膜和牙槽骨CAD模型

图5分别为超弹性模型和线弹性模型下的牙周膜的应力响应云图．从图中可看出两者的应力分布存在较大的差异,线弹性模型牙周膜的应力分布相对于超弹性模型的较均匀,且最大应力大于超弹性模型的最大应力．然而,由于牙周膜几何结构的复杂性致使应力分布情况并不均匀,这表明采用非线性超弹性模型来模拟计算牙周膜的生物力学响应比使用线弹性模型更为合理．两者应力主要集中分布在牙周膜牙颈处和根尖部位,其最大应力出现在舌侧牙周膜牙颈处,为压应力,同一侧根尖处产生拉应力,而唇侧的应力情况则相反,研究结果与文献[2,12]一致．此外,在超弹性牙周膜根尖和牙颈之间的部分存在局部的应力集中．2个模型的最大主应力值分别为2.7190MPa和0.1451MPa．

图5 超弹性和线弹性模型牙周膜应力对比

图6为正畸力作用下的超弹性牙周膜的应变响应,其分布情况与应力相似．

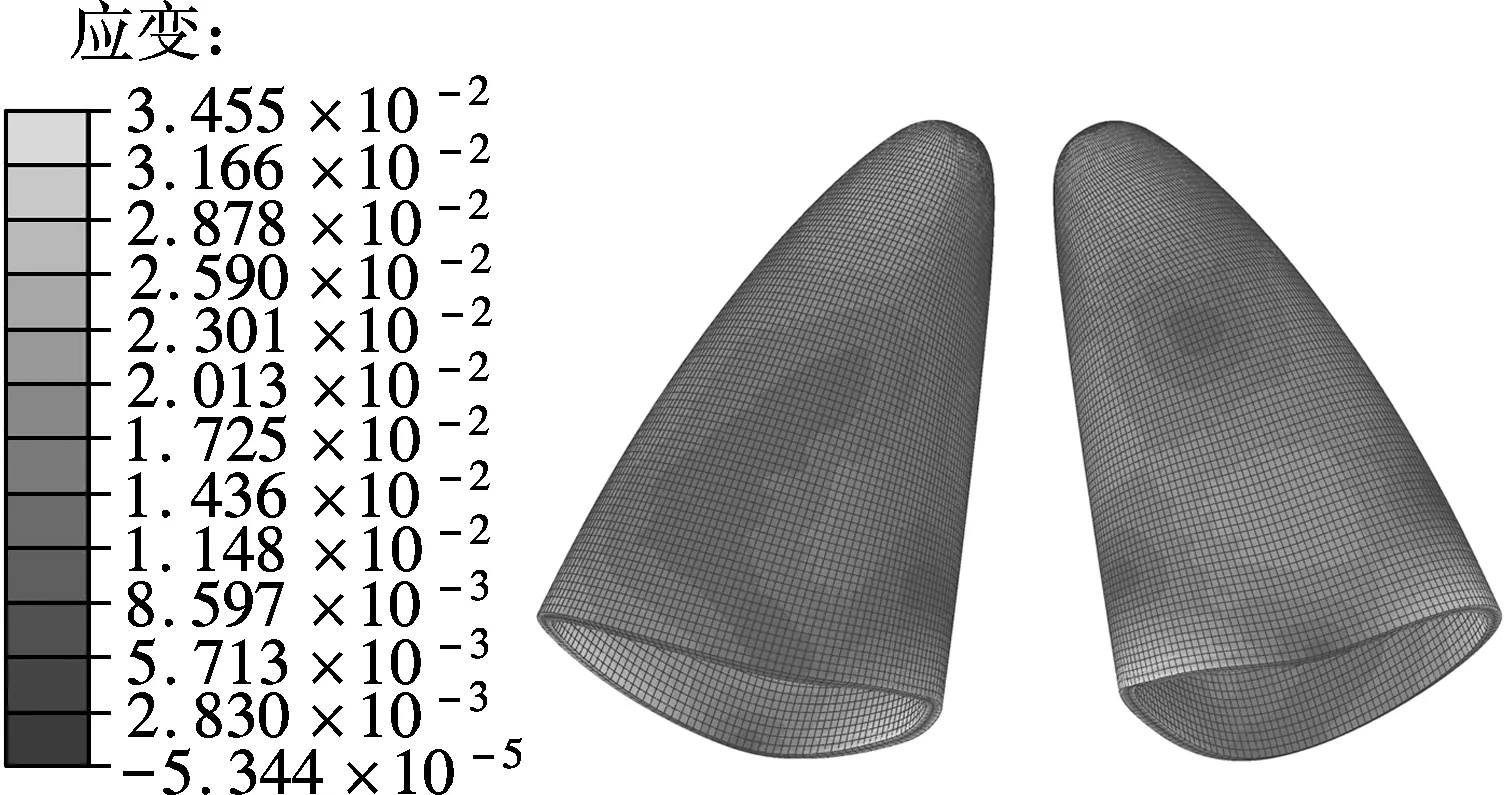
图6 超弹性模型牙周膜应变

4 结语

由于牙周膜拉应力-应变关系呈现非线性的指数形式,本文将Mooney-Rivlin指数模型引入到牙周膜生物力学响应的模拟分析中,利用人体牙周膜拉伸实验数据,拟合出模型的材料参数.因实验数据较少且发散性大,导致数据拟合的相对误差较大,会影响模型对牙周膜力学特性的描述能力,因此,较为精确可靠的力学实验数据是牙周膜力学模型研究亟待解决的问题．在超弹性指数模型本构关系的基础上,开发了模型的ABAQUS用户子程序UHYPER,通过拉伸实验测试数据的模拟计算验证了子程序开发的正确性,同时该子程序具有比较理想的计算精度,从而为自定义的本构模型开发提供了借鉴．Mooney-Rivlin指数模型能够较好地描述牙周膜的瞬时弹性响应．

牙周膜不仅表现出瞬时的超弹性,还表现为与时间历程相关的黏弹性,后续工作重点是如何将牙周膜的超弹性与黏弹性结合起来,建立一个能够全面描述牙周膜生物力学特性的黏-超弹性本构模型,同时开展人体体内实验测试研究来进一步验证和评价所构建的本构模型．

)

[1]Kawarizadeh A, Bourauel C, Jager A. Experimental and numerical determination of initial tooth mobility and material properties of the periodontal ligament in rat molar specimens [J].EurJOrthod,2003,25(6): 569-578.

[2]Wu Bin, Tang Wencheng, Yan Bin. Study on stress distribution in periodontal ligament of impacted tooth based on hyperelastic model [C]//IEEEInformationEngineeringandComputerScience.Wuhan, China,2009: 1550-1553.

[3]Lu Hongfei, Mai Zhihui, Chen Qi, et al. Initial stress distribution of the maxillary anterior teeth, periodontal ligament and alveolar bone by different intruding loadings: a three-dimensional finite element analysis [J].JournalofClinicalRehabilitativeTissueEngineeringResearch,2011,15(48): 8964-8967.

[4]Hohmann A, Kober C, Young P, et al. Influence of different modelling strategies for the periodontal ligament on finite element simulation results [J].AmJOrthodDentofacialOrthop, 2011,139(6):775-783.

[5]魏志刚,汤文成,严斌,等.基于黏弹性模型的牙周膜生物力学研究[J].东南大学学报:自然科学版,2009,39(3):484-489.

Wei Zhigang,Tang Wencheng,Yan Bin,et al. Biomechanical analysis of periodontal ligament based on viscoelastic model [J].JournalofSoutheastUniversity:NaturalScienceEdition,2009,39(3): 484-489.(in Chinese)

[6]Natali A N, Carniel E L, Pacan P G, et al. Experimental-numerical analysis of minipig’s multi-rooted teeth [J].JournalofBiomechanics,2007,40(8):1701-1708.

[7]Zhan Gao, Lister K, Desai J P. Constitutive modelling of liver tissue: experiment and theory [J].AnnalsofBiomedicalEngineering,2010,38(2):505-516.

[8]Chui C, Kobayashi E, Chen X,et al. Compression and elongation experiments and non-linear modelling of liver tissue for surgical simulation [J].MedBiolEngComput,2004,42(6):787-798.

[9]Yoshida Noriaki, Koga Yoshiyuki, Peng Chien-Lun, et al. In vivo measurement of the elastic modulus of the human periodontal ligament [J].MedEngPhy,2001,23(8):567-572.

[10]Hibbitt D, Karlsson B, Sorensen P.ABAQUS/standarduser’smanual[M]. Pawtucket, RI,USA: Dassault Systèmes Simulia Corp, 2010.

[11]Tanne K, Yoshida S, Kawata T, et al. An evaluation of the biomechanical response of the tooth and periodontium to orthodontic forces in adolescent and adult subjects [J].BritishJournalofOrthodontics, 1998,25(2):109-115.

[12]Cattaneo P M, Dalstra M, Melsen B. Strain in periodontal ligament and alveolar bone associated with orthodontic tooth movement analyzed by finite element [J].OrthodCraniofacRes,2009,12(2):120-128.