我国杉木通用性立木生物量模型研究

曾伟生

(国家林业局调查规划设计院，北京 100714)

我国杉木通用性立木生物量模型研究

曾伟生

(国家林业局调查规划设计院，北京 100714)

以我国南方地区的最重要针叶树种杉木为研究对象，综合利用非线性混合模型、哑变量模型和误差变量联立方程组方法，建立了适合杉木不同生长区域(总体)应用的一体化一元和二元地上生物量方程及根茎比函数。结果表明： 不同总体的地上生物量模型之间存在显著差异，总体(一)的估计值要大于总体(二)，而地下生物量则差异不明显；地上和地下生物量方程的平均预估误差分别在5%和10%以内，可应用于不同区域的杉木林生物量估计。

地上生物量；根茎比；非线性混合模型；哑变量模型；误差变量联立方程组；杉木

在应对全球气候变化的大背景下，森林生态系统的固碳能力日益引起广泛关注。森林固碳能力的大小与森林碳储量是紧密相关的，而森林碳储量就等于森林生物量与含碳系数之积。相对而言含碳系数比较稳定(一般可近似取0.5)，森林生物量估计便成为最首要的问题。估计生物量最常用的方法是采用生物量换算因子或生物量方程，因此建立各树种的生物量方程便成为最重要的基础工作。关于建立生物量方程的方法，国内外可参考的文献很多[1-15]。需要重点关注的是，有学者采用误差变量联立方程组(或称度量误差模型)方法建立与立木材积相容的立木生物量方程[16-17]，还有人利用线性混合模型和哑变量模型建立不同尺度或不同区域的立木生物量方程[18-20]，都取得了良好效果。近年来，非线性混合模型方法在林业领域已逐渐得到应用[21-23]。在建立适合不同区域的通用性立木生物量方程时，混合模型和哑变量模型方法，究竟哪一种更好？如何综合利用混合模型、哑变量模型和误差变量联立方程组方法，建立相容性立木生物量方程？本文以我国南方地区的最重要针叶树种杉木(Cunninghamialanceolata)为研究对象，对非线性混合模型和哑变量模型进行了对比分析，同时结合误差变量联立方程组方法，建立了适合不同区域应用的相容性地上和地下生物量方程，可为我国杉木林生物量估计提供计量依据。

1 材料与方法

1.1 材料

本文所用材料为2009年和2010年全国连清生物量调查建模项目采集的301株杉木样本数据。按照部颁标准《立木材积表》[24]中的总体划分，该样本涉及2个建模总体：其一是包括湖南、湖北、广东、广西、浙江、安徽、江苏、四川、贵州等省区，样木数为151株；其二是包括江西、福建2省，样木数为150株。每个建模总体的样木数都均匀分配在2，4，6，8，12，16，20，26，32cm及38cm以上10个径阶，每个径阶的样木数也均匀分配在3～5个树高级内。每株样木都实测胸径、树高，并通过区分求积法测定立木材积；同时分别树干、树皮、树枝、树叶称其鲜质量，并取样带回实验室测定干质量，最后再推算各部分干质量及地上部分总干质量(生物量)，其中约1/3的样木还同时测定了地下生物量。表1为杉木地上生物量和地下生物量样本数据的基本情况。

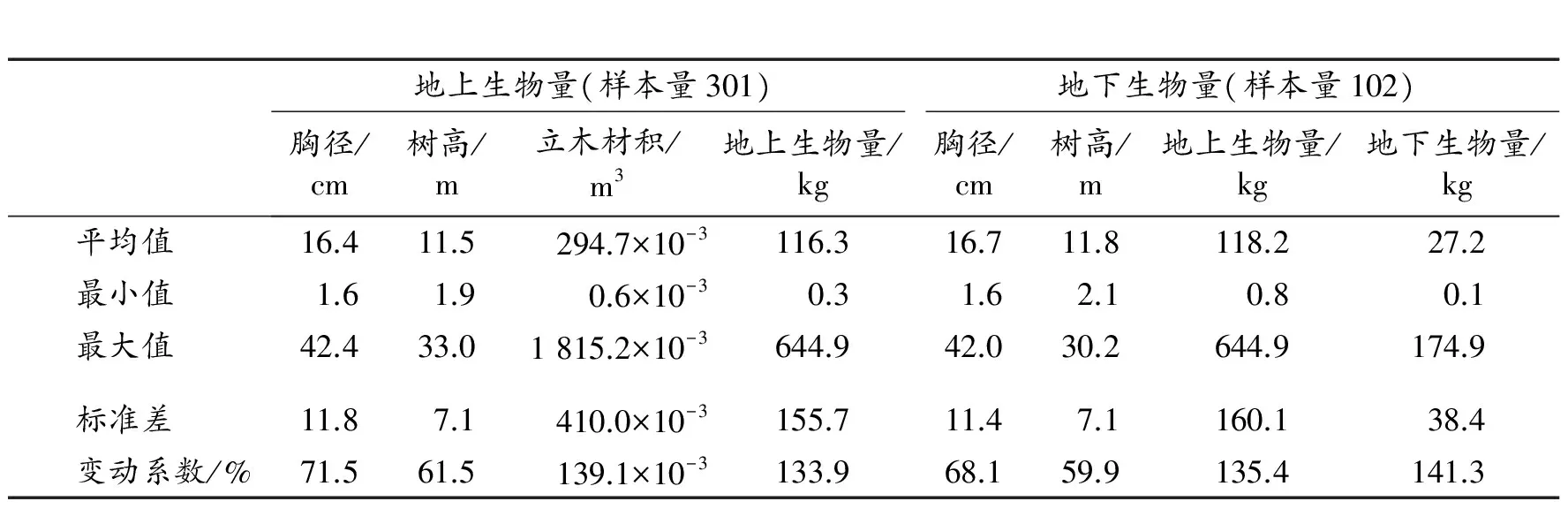
表1 杉木建模样本数据的基本情况

1.2 方法

立木生物量方程的常用结构形式为[1,4,15]：

y=β0x1β1x2β2…xjβj+ε

(1)

式中：y为生物量，xj为胸径、树高等反映林木大小的变量，βj为参数，ε为误差项。由于生物量数据均存在明显的异方差性，参数估计时必须采取消除异方差的措施。本文采用加权回归方法，并利用普通回归估计的残差推导的特定权函数进行加权回归[25]。由于基于胸径的一元模型和基于胸径与树高的二元模型应用最为广泛，本文将以树高—胸径回归模型为桥梁，通过利用非线性误差变量联立方程组[26]，同时建立一元和二元立木生物量模型。

1.2.1 非线性混合模型

前已述及，我国杉木分布区域划分为2个总体。各总体范围内的降水、温度、土壤等自然地理条件存在差异，导致对立木生物量模型产生影响。由于这种影响是多因素综合产生的，具有很大程度的不确定性或随机性，因此，可将反映不同区域或总体范围的变量z定义为随机效应变量，而将胸径D、树高H等反映林木大小的变量定义为固定效应变量。同时包含固定效应变量和随机效应变量的二元立木生物量混合模型的基本形式表示为：

M=(a0+u0z)D(a1+u1z)H(a2+u2z)+ε

(2)

式中：M为生物量，ai为固定参数，ui为随机参数。其中，随机参数ui的数学期望值为0，且相互独立，即：E(ui)=0，cov(ui,uj)=0(i≠j)。随机参数ui是否与0有显著差异，通过随机效应的显著性检验结果得出。

1.2.2 哑变量模型

与(2)式对应的哑变量二元立木生物量模型的基本形式表示为：

M=(a0+v0z)D(a1+v1z)H(a2+v2z)+ε

(3)

式中：z为哑变量，vi为相应的特定参数(或局部参数)，其它符号同式(2)。为了区别起见，在哑变量模型中把对应于混合模型的固定参数称为通用参数(或全局参数)。为直观理解不同尺度模型(全局模型和局部模型)之间的相容性，也便于与混合模型对照，保证∑vi=0，处理哑变量时将常规的(0，1)设置调整为(1，-1)，即：属于总体1的样本，取z=1；属于总体2的样本，取z=-1。由于该条件的限制，2个特定参数中只有1个需要直接估计。特定参数vi是否与0有显著差异，通过参数估计值的显著性检验结果得出。

1.2.3 误差变量联立方程组

在确定混合模型或哑变量模型的最终形式后，为了得到与材积相容的地上生物量模型及其生物量转换因子函数，以及与地上生物量相容的地下生物量模型及其根茎比函数，并实现一元和二元模型的一体化估计，需要采用误差变量联立方程组方法，对多个方程进行联合估计。建立相容性地上生物量模型采用以下形式的联立方程组：

(4)

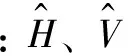
(5)

它们之间的参数存在以下关系：

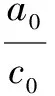
(6)

在上述(4)式～(6)式中，如果a2，c2和e2均取0，即在公式中去掉与树高相关的乘积项，就变成了一元模型。

同样，建立相容性地下生物量模型采用以下形式的联立方程组：

(7)

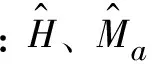
(8)

它们之间的参数存在以下关系：

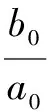
(9)

同理，在上述(7)式～(9)式中，如果a2，b2和f2均取0，就变成了一元模型。

1.2.4 模型评价

模型评价指标采用确定系数(R2)、估计值的标准误(SEE)、平均预估误差(MPE)、总相对误差(TRE)、平均系统误差(MSE)和平均百分标准误差(MPSE)6项指标，具体计算公式参见有关文献[27]。

2 结果与分析

2.1 非线性混合模型与哑变量模型的对比分析

2.1.1 利用301株样木数据进行对比分析

利用我国南方杉木2个建模总体的301株样木的地上生物量数据，采用ForStat软件中的“非线性混合模型”和“一元非线性回归”方法[26]，分别拟合式(2)和式(3)及其简化形式，结果见表2。

从表2结果看，非线性混合模型的固定参数与哑变量模型的通用参数ai相差不大，但随机参数ui与特定参数vi则有一定差异，且其绝对值几乎都是哑变量模型的特定参数大于对应的混合模型随机参数，但幅度多数在10%～15%之间，仅个别超过40%。总体而言，对于地上生物量，非线性混合模型与哑变量模型之间的差异比较小。

另外，还利用立木材积数据作了同样的对比分析。结果表明： (1)混合模型不论是3个随机参数还是2个随机参数，其随机效应均不显著，仅当存在1个随机参数u0时才呈弱显著性(0.10水平)；(2)哑变量模型含3个特定参数时，参数v0极显著(0.01水平)，参数v1不显著，参数v2较显著(0.10水平)；只含2个特定参数v0和v2时，前者极显著(0.01水平)，后者显著(0.05水平)。因此，立木材积非线性混合模型与哑变量模型之间的差异非常显著。

2.1.2 利用102株样木数据进行对比分析

表2 地上生物量非线性混合模型和哑变量模型的参数估计值(n=301)

利用杉木2个建模总体的102株样木的地上生物量数据，采用ForStat软件中的“非线性混合模型”和“一元非线性回归”方法[26]，分别拟合式(2)和式(3)及其简化形式，结果见表3。

从表3结果看，非线性混合模型的固定参数与哑变量模型的通用参数ai相差大于表2，尤其是随机参数ui与特定参数vi之间的差异更大。混合模型的随机参数仅u0与0有显著差异，u1和u2的绝对值均很小，近乎为0；而哑变量模型的特定参数除v0与0有显著或极显著差异外，含2个特定参数的模型中，v1在统计上也较显著。仅当两个模型都只含1个随机参数或特定参数时，其差异才降至10%左右；否则，非线性混合模型的随机参数与哑变量模型的特定参数相差均在5倍以上。

另外，还利用地下生物量数据作了同样的对比分析。结果表明： ①混合模型的3个随机参数均为0，即表明总体1和总体2之间的差异是随机影响造成的，二者在统计上无显著差异；②哑变量模型的3个特定参数中，参数v0和v1显著(0.05水平)，参数v2较显著(0.10水平)。因此，地下生物量非线性混合模型与哑变量模型之间的差异也非常显著。

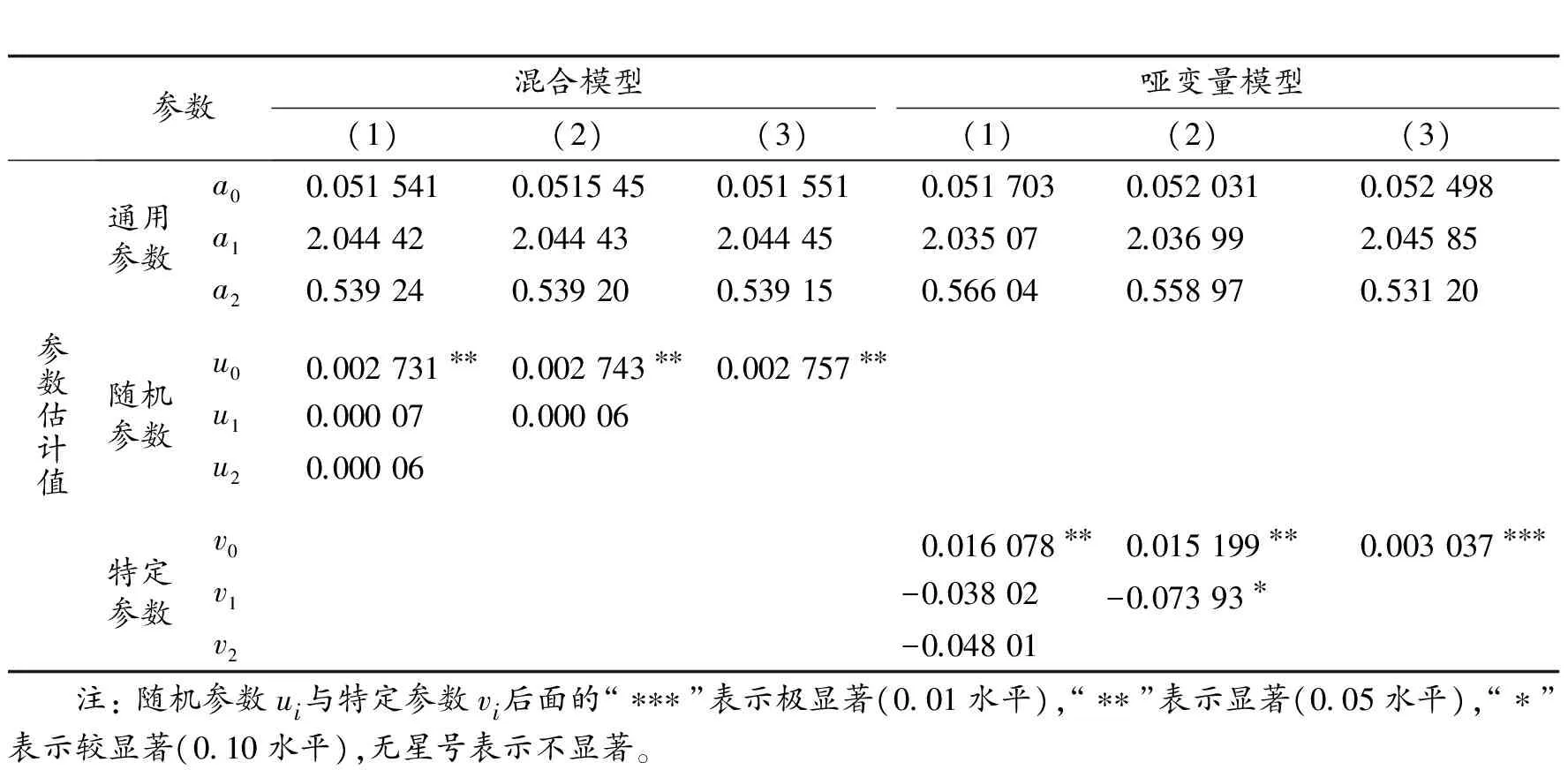
表3 地上生物量非线性混合模型和哑变量模型的参数估计值(n=102)

2.2 相容性地上生物量模型及其转换因子函数

利用杉木2个建模总体的301株样木的数据，采用ForStat软件中的“非线性误差变量联立方程组”方法[26]，分别拟合联立方程组(4)，其中立木材积方程和地上生物量方程的通用性模型形式，分别采用2.1.1节中的混合模型和哑变量模型结果，见表4和表5。

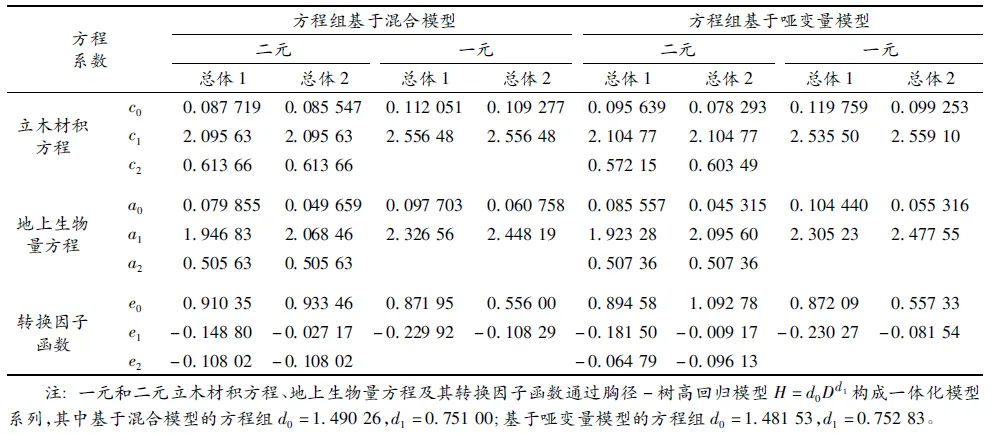
表4 相容性地上生物量模型及其转换因子函数的参数估计值对比

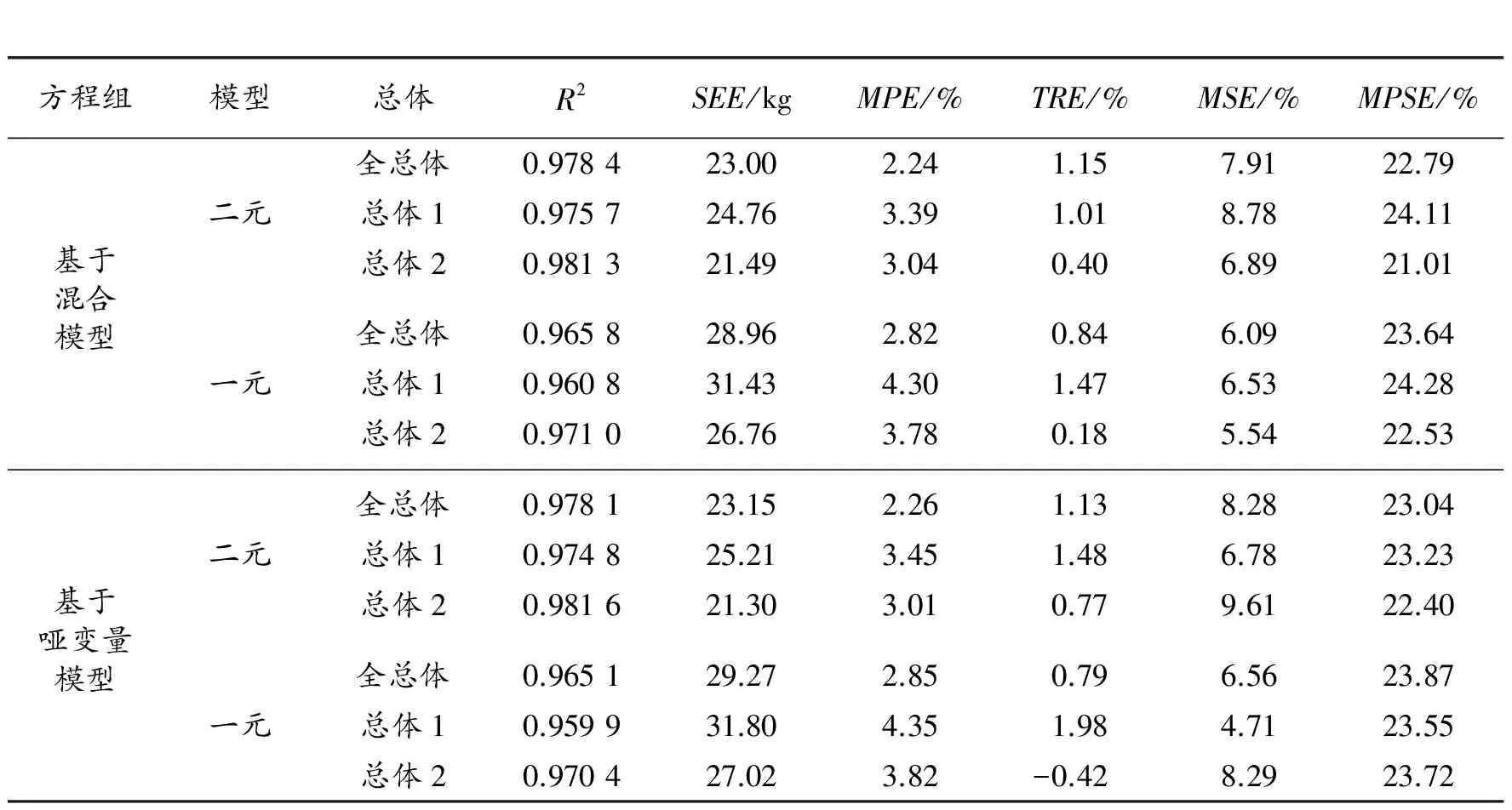
表5 相容性地上生物量模型的统计指标对比

从表4两个方程组的结果看，地上生物量方程完全类似，总体1和总体2仅参数a2相同，参数a0和a1不同，而基于混合模型的方程组参数估计值，总体之间的差异要小一些；立木材积方程则有所不同，基于混合模型的方程组，总体之间仅参数c0有差异，参数c1和c2均相同，而基于哑变量模型的方程组，总体之间仅二元方程的参数c1相同，其他参数均有差异；对于转换因子函数，两组模型的结果略有不同，其中基于混合模型的方程组参数估计值，总体之间的差异要小一些。从表5的6项统计指标看，基于混合模型的方程组要优于哑变量模型方程组。因此，地上生物量模型应该选用基于混合模型的联立方程组结果。

2.3 相容性地下生物量模型及其根茎比函数

利用杉木2个建模总体的102株样木的数据，采用ForStat软件中的“非线性误差变量联立方程组”方法[26]，分别拟合联立方程组(7)，其中地上生物量和地下生物量方程的通用性模型形式，分别采用2.1.2节中的混合模型和哑变量模型结果，见表6和表7。

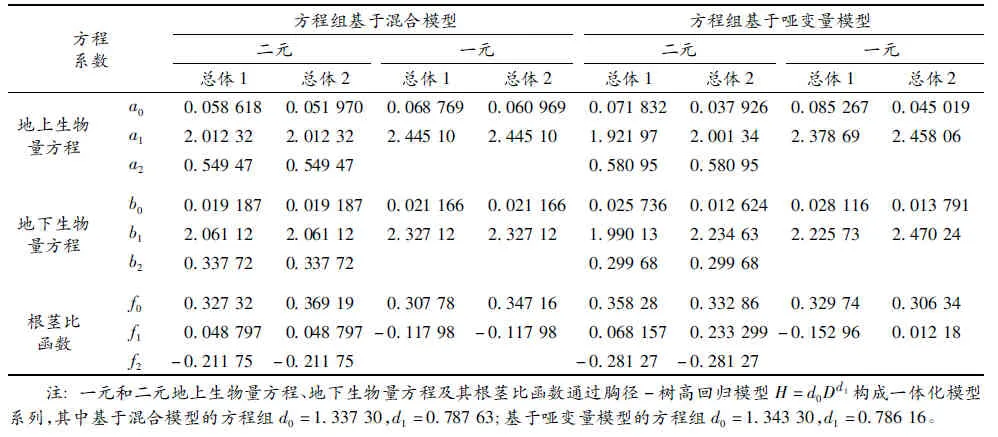
表6 相容性地下生物量模型及其根茎比函数的参数估计值对比

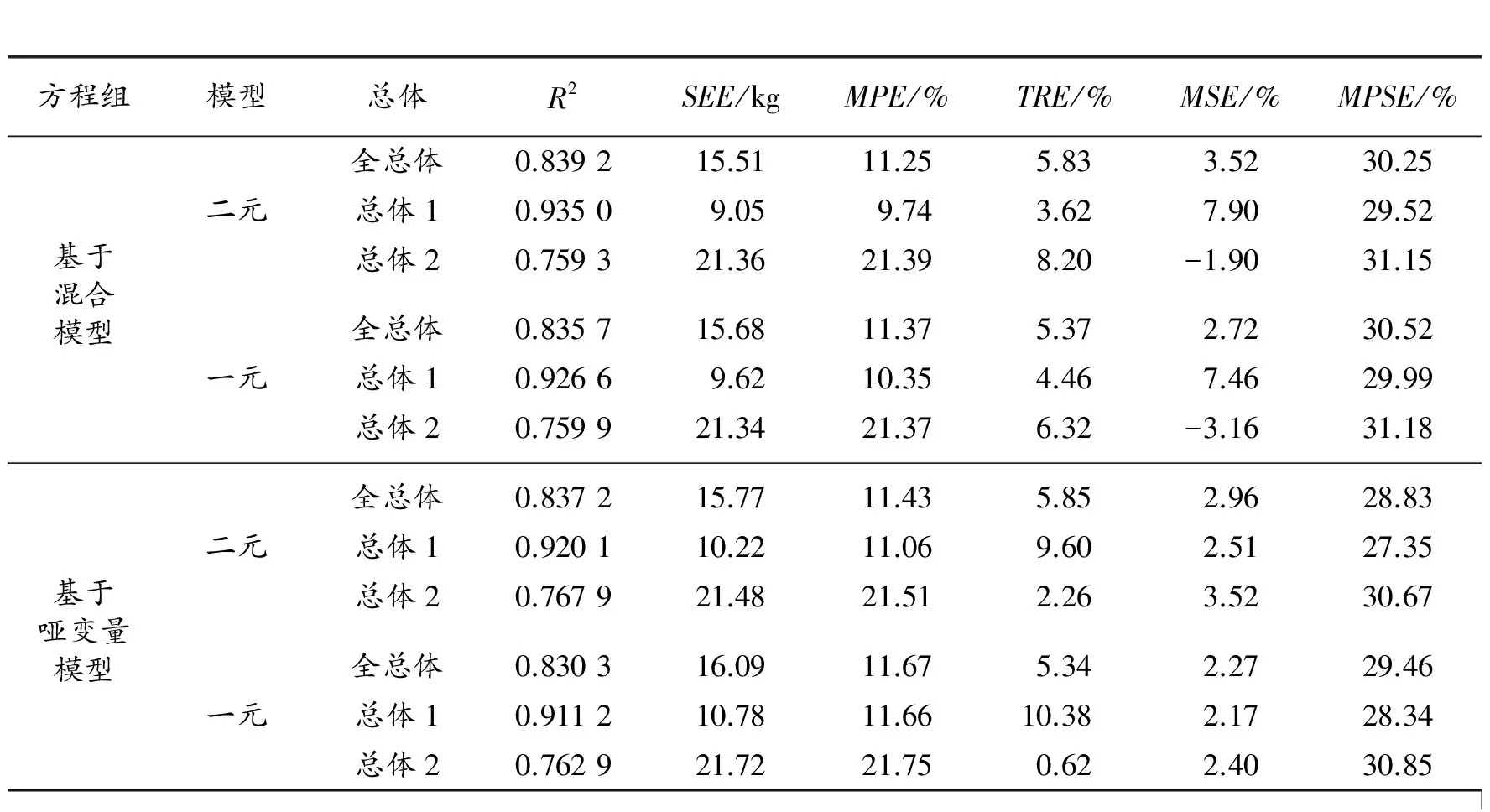
表7 相容性地下生物量模型的统计指标对比

从表6两个方程组的结果看，基于混合模型的方程组，地下生物量方程总体1和总体2没有差异，而根茎比函数总体1和总体2仅参数f0不同；基于哑变量模型的方程组，总体之间仅参数b2及f2相同，其他参数均有差异，而且这种差异导致根茎比函数的参数出现异常，如参数f1出现了总体1为负而总体2为正的情况。从表7的6项统计指标看，基于混合模型的方程组多数指标要优于哑变量模型方程组。因此，地下生物量模型也应该选用基于混合模型的联立方程组结果。

需要注意的一点是，由于表6中的地上生物量方程与表4的结果有所不同，尤其是不同总体模型的参数变化规律存在差异，会相应地影响到根茎比函数的变化规律。为此，对基于混合模型的地下生物量非线性误差变量联立方程组(7)重新进行拟合，其中地上生物量方程的通用性模型形式与表4相同，且树高曲线取相同参数值。重新拟合后的参数估计值见表8。通过与表6结果的对比，可近似将表8的结果看成是前述2个方程组的折中处理方案，也被认为是最佳结果。对应于表7中全总体二元模型的6项统计指标结果如下：R2=0.8369，SEE=15.62，MPE=11.33%，TRE=6.89 %，MSE=2.88 %，MPSE=29.98 %。

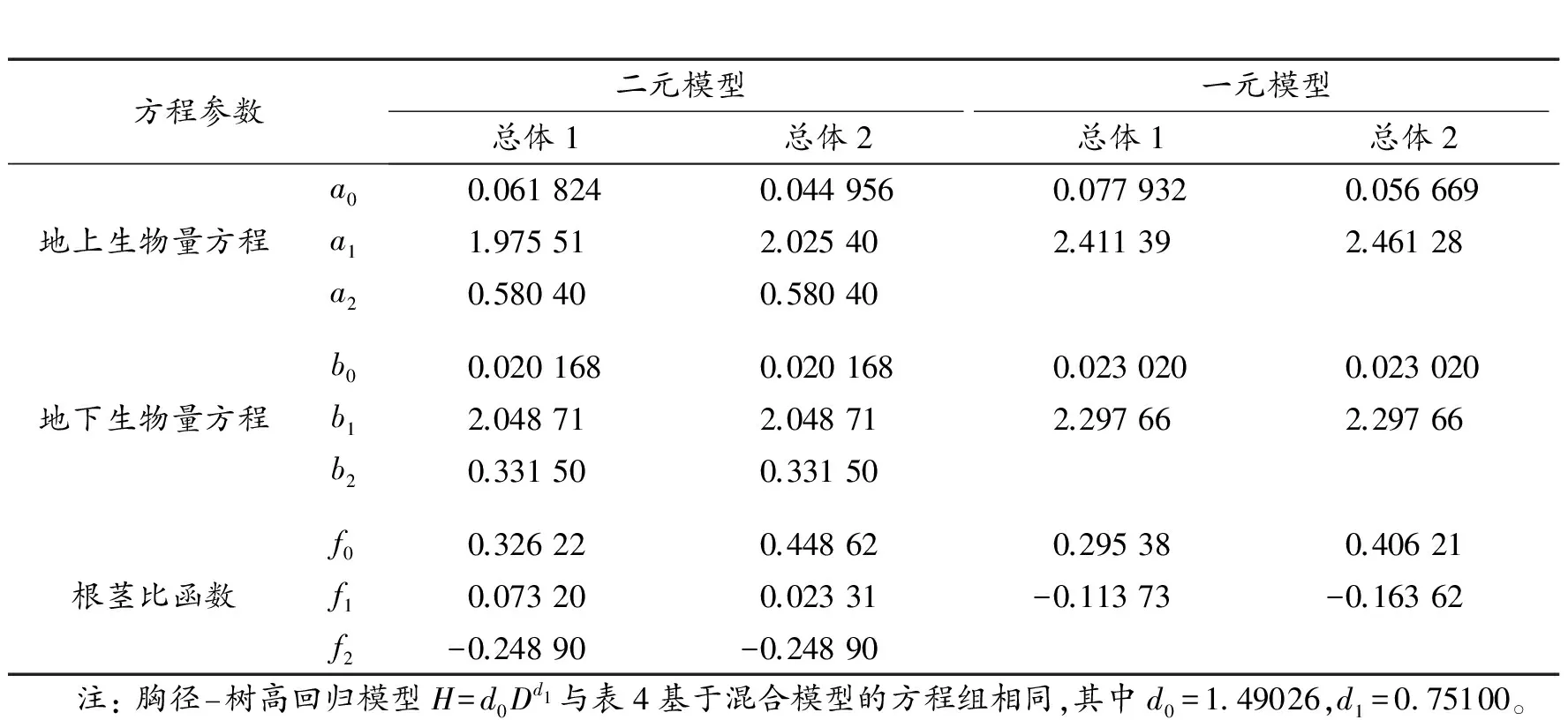
表8 相容性地下生物量模型及其根茎比函数的参数估计值

在实际应用时，采用表4中基于混合模型的联立方程组中的地上生物量方程及表8中的根茎比函数，分别计算杉木地上和地下生物量及总生物量。其中，地下生物量方程可由地上生物量方程与根茎比函数相乘得到：

总体1 二元模型：Mb=0.026 050D2.02002H0.25674

一元模型：Mb=0.028860D2.21283

总体2二元模型：Mb=0.022278D2.09176H0.25674

一元模型：Mb=0.024681D2.28457

由于地下生物量与地上生物量相关紧密，可以把建立表4中地上生物量模型的301株样木视为一重样本，把建立表8中地下生物量模型的102株样木视为二重样本，按(10)式计算最后综合的地下生物量模型的平均预估误差：

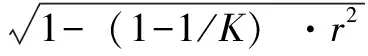
(10)

式中：K为一重样本与二重样本单元数之比，此处为2.95；r为二重样本地下生物量与地上生物量之间的相关系数，经计算r=0.9183；MPE2为利用二重样本建立的地下生物量模型估计值的平均预估误差，对全总体二元模型为11.33%；MPE1为综合一重样本后得到的地下生物量模型估计值的平均预估误差，对全总体二元模型经计算为7.54%。

立木总生物量的平均预估误差可根据地上生物量和地下生物量的误差，按和的误差传播公式计算。如对于全总体二元模型，按地上生物量平均预估误差2.24%、地下生物量平均预估误差7.54%，用和的误差传播公式进行计算，林木总生物量的平均预估误差约为2.00%。

3 讨论与结论

混合模型和哑变量模型在林业数表领域的应用都比较广。混合模型更多适用于同时具有确定性变量和不确定性变量(或随机变量)的情形，而哑变量模型是处理定性因子或分类变量的一种常用方法。对于解决不同总体之间的相容性问题，建立全总体范围的通用性模型，这两种方法都是有效的[18-20]。但是，混合模型与哑变量模型方法究竟哪种更合适，一直都少有定论。Wang等[28]认为，如果类型数量少(如10个以下)，则选择哑变量模型可能较好；如果类型数量多，而且每个类型包含的样本量又少，则一般推荐混合模型；如果每个类型的样本量都较大，则选择哪个模型都无关紧要。并以建立优势高模型为例进行了对比分析，认为两种方法都适用于建立带有特定参数或地方参数的模型，而且二者的效果基本相当；就拟合效果而言，哑变量方法可能略好；就预估效果而言，混合模型方法更合适。Fu等[29]以建立我国南方马尾松不同尺度立木生物量模型为例，对混合模型与哑变量模型方法进行了对比，认为当各个类型的样本单元数足够多时，采用哪种方法都是可行的；当各个类型的样本单元数较少时，采用混合模型较为合适；总体而言，混合模型方法具有较大的灵活性和适应性。本研究通过利用2种样本量的数据进行建模对比分析，也得到了类似的结论。采用301株样木建立通用性地上生物量方程，混合模型和哑变量模型差异不大；但建立通用性立木材积方程时，混合模型和哑变量模型之间存在显著差异；而采用102株样木来建立地上和地下生物量模型，则均具有明显不同的结果。根据分析，两种方法建模结果的差异除了受样本量的影响以外，还与各个类型之间研究对象本身的差异大小有关。如本例两个总体之间的立木材积、地上生物量和地下生物量，从数据反映的情况看，除地上生物量差异较大以外，立木材积和地下生物量之间差异较小，所以即使样本量达到300以上，两种方法的建模结果仍然存在显著差异。从建模结果分析来看，混合模型相当于把建模数据各类型之间的差异分解成为两部分：一部分是类型之间固有的差异，另一部分是随机误差引起的差异；而哑变量模型则把建模数据各类型之间的差异全部当成本身固有的差异，未考虑随机误差的影响。因此，混合模型方法是值得推荐应用的更有效方法。

本文在对混合模型和哑变量模型进行对比分析的基础上，确定了我国南方杉木地上生物量和地下生物量模型不同总体参数之间的差异，设计了适用于不同总体的通用性模型，并通过非线性误差变量联立方程组方法，构建了相容性地上生物量模型及其转换因子函数，以及相容性地下生物量模型及其根茎比函数，为杉木林的生物量估计提供了计量依据。不论是一元还是二元模型，地上生物量估计的平均预估误差均在5 %以内，地下生物量估计的平均预估误差也能达到10 %以内，完全可满足森林生物量估计的精度要求，可以应用于不同总体范围的杉木林生物量估计。

[1] Parresol B R. Assessing Tree and Stand Biomass: A Review with Examples and, Critical Comparisons[J].Forest Science，1999，45(4)：573-593.

[2] Jenkins J C, Chojnacky D C, Heath L S, et al. National-scale Biomass Estimators for United States Tree Species[J]. Forest Science，2003，49(1)：12-35.

[3] Bi H, Turner J, Lambert M J. Additive Biomass Equations for Native Eucalypt Forest Trees of Temperate Australia[J].Trees，2004，18(4)：467-479.

[5] Snorrason A, Einarsson S F. Single-tree Biomass and Stem Volume Functions for Eleven Tree Species Used in Icelandic Forestry[J].Icelandic Agric Sci，2006，19：15-24.

[6] Muukkonen P. Generalized Allometric Volume and Biomass Equations for Some Tree Species in Europe[J].Eur J Forest Res，2007，126：157-166.

[8] Návar J. Allometric Equations for Tree Species and Carbon Stocks for Forests of Northwestern Mexico[J].Forest Ecology and Management。2009，257：427-434.

[9] 骆期邦,曾伟生,贺东北,等.立木地上部分生物量模型的建立及其应用研究[J].自然资源学报,1999,14(3):271-277.

[10] 张会儒,赵有贤,王学力,等.应用线性联立方程组方法建立相容性生物量模型研究[J].林业资源管理, 1999 (6):63-67.

[11] 唐守正,张会儒,胥辉.相容性生物量模型的建立及其估计方法研究[J].林业科学,2000,36(专刊1):19-27.

[12] 胥辉,刘伟平.相容性生物量模型研究[J].福建林学院学报, 2001，21(1):18-23.

[13] 刑艳秋,王立海.基于森林调查数据的长白山天然林森林生物量相容性模型[J].应用生态学报, 2007， 18 (1)：1-8.

[14] 程堂仁,冯菁,马钦彦,等.小陇山油松林乔木层生物量相容性线性模型[J].生态学杂志，2008， 27(3):317-322.

[15] 曾伟生. 全国立木生物量方程建模方法研究[D].北京：中国林业科学研究院, 2011.

[16] 王为斌,党永峰,曾伟生.东北落叶松相容性立木材积和地上生物量方程研建[J].林业资源管理, 2012 (2): 69-73.

[17] Zeng W S, Tang S Z. Modeling compatible single-tree aboveground biomass equations for masson pine (Pinusmassoniana) in southern China[J].Journal of Forestry Research，2012，23(4)：593-598.

[18] 曾伟生,唐守正.利用混合模型方法建立全国和区域兼容性立木生物量方程[J].中南林业调查规划, 2010,29(4):1-6.

[19] Zeng W S, Zhang H R, Tang S Z.Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales—a case study for masson pine (Pinusmassoniana) in southern China[J].Can J For Res, 2011,41(7)：1547-1554.

[20] 曾伟生,唐守正,夏忠胜,等.利用线性混合模型和哑变量模型方法建立贵州省通用性生物量方程[J]. 林业科学研究, 2011，24(3): 285-291.

[21] Meng S X, Huang S, Lieffers V J,et al.Wind speed and crown class influence the height-diameter relationship of lodgepole pine:nonlinear mixed effects modeling[J]. Forest Ecology and Management, 2008，256：570-577.

[22] 符利勇, 张会儒, 唐守正. 基于非线性混合模型的杉木林优势木平均高[J].林业科学，2012，48(7): 66-71.

[23] 符利勇, 张会儒, 李春明,等. 非线性混合效应模型参数估计方法分析[J]. 林业科学, 2013，49(1): 114-119.

[24] 中华人民共和国农林部. LY208—77立木材积表[S].北京:技术标准出版社，1978.

[25] 曾伟生，唐守正.非线性模型对数回归的偏差校正及与加权回归的对比分析[J].林业科学研究，2011，24(2)：137-14 .

[26] 唐守正,郎奎建,李海奎.统计和生物数学模型计算：ForStat教程[M].北京:科学出版社，2008.

[27] 曾伟生,唐守正.立木生物量模型的优度评价和精度分析[J].林业科学，2011，47(11)：106-113.

[28] Wang M, Borders B E, Zhao D. An empirical comparison of two subject-specific approaches to dominant heights modeling the dummy variable method and the mixed model method[J].Forest Ecology and Management, 2008，255: 2659-2669.

[29] Fu L Y, Zeng W S, Tang S Z,et al. Using linear mixed model and dummy variable model approaches to construct compatible single-tree biomass equations at different scales-A case study for Masson pine in southern China[J].Journal of Forest Science, 2012, 58(3):101-115.

GeneralizedTreeBiomassEquationsofChineseFirinChina

ZENG Weisheng

(Academy of Forest Inventory and Planning, State Forestry Administration，Beijing 100714，China)

Taking the most important coniferous species of southern China, Chinese fir (Cunninghamialanceolata), as the study object, the integrated one-and two-variable aboveground biomass equations and root-to-shoot ratio functions suitable for generalized application in two regions (population areas) were constructed using nonlinear mixed model, dummy variable model and error-in-variable simultaneous equation approach. The results showed that aboveground biomass models of the two populations are significantly different, the projected estimates for population I being more than those for population II, while belowground biomass models are not; the mean prediction errors (MPE’s) of above-and below-ground biomass equations are less than 5% and 10% respectively, which means the biomass equations could be applied for estimation of Chinese fir forest biomass in the regions.

aboveground biomass；root-to-shoot ratio；nonlinear mixed model；dummy variable model；error-in-variable simultaneous equation；Cunninghamialanceolata

2013-08-20

曾伟生(1966-)， 男，博士，教授级高工，主要从事森林资源监测与林业数表编制工作。

S711

A

1003-6075(2013)04-0004-08