基于时频图像形态学的雷达信号IF估计

白 航，李传兵，李富军，徐 文

（中国人民解放军61906部队，河北 廊坊065001）

0 引言

雷达信号是一种非平稳信号，传统的Fourier频率不能对其进行有效描述，瞬时频率（IF）反映了信号频率随时间的变化规律，是表征非平稳信号的重要参数。因此IF估计是分析和研究雷达信号的一项基本任务。时频分析是目前IF 估计研究中较为普遍和有效的方法［1-7］，根据信号的时频聚集特性，信号的能量在时频面上将沿着IF的方向产生聚集，从而可以采用时频分布峰值检测法对信号进行IF 估计［3-4］。在信噪比较高的情况下，时频分布峰值法能准确估计出的信号IF，但随着信噪比的降低，时频分布不能准确地描述信号的能量分布，因而对于IF的估计性能也大大降低。文献［5］提出了自适应窗长WVD（Wigner-Ville Distribution）峰值检测法，在计算WVD 时选择一个最优窗长使得IF 估计的均方根误差最小。为了避免初始估计中出现大的偏差，一般采用较窄的窗长，然而随着信噪比的降低，较窄的数据窗长会使得时频分布的峰值不在信号自项区域的概率增大，从而导致IF估计出现较大的偏差。文献［6］综合利用Gabor变换WVD 的特点，提出一种自适应时频分布，然后采用时频分布一阶矩方法估计信号IF，该方法有效降低了运算量，但在低信噪比条件下信号IF估计效果也不是很理想。

将图像处理技术和信号处理相结合，为调频信号IF估计提供了新的视角。针对较低信噪比条件下以及多分量信号的IF估计，本文首先对信号进行时频变换，并将其转化为灰度图；然后检测信号的起止频率，剪切出信号时频分布的有效区域［8］；最后采用形态学图像处理方法估计出信号的IF。将信号转化为时频图像后，可以进一步利用图像处理中的降噪算法，增强信号的前景像素，降低噪声对IF估计的影响。具体流程如图1所示。

图1 本文IF估计方法流程图

1 MBD时频分布

雷达信号是一种典型的非平稳信号，传统的时域和频域分析方法只能获取有限的信号信息，时频分析反映了信号能量随时间和频率的分布，能在时频域更为精确地描述信号。本文应用时频分析方法估计信号的IF曲线，为了提升估计效果，需要时频分布具有较高的时频聚集性，使得信号时频能量聚集在IF曲线附近，同时又能尽可能消除交叉项的影响。Cohen类时频分布通过核函数对WVD 进行平滑，在抑制交叉项和保持高时频分辨率之间做一个折中，其定义为：

Hussainn和Boashash 于2002年提出一种改进的B分布（MBD）的时频分布方法［7］，其核函数为：

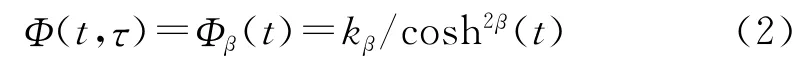
式中，kβ＝Γ（2β）／（22β-1Γ2（β）），Γ 为gamma函数，即：MBD 能满足时频分布的大多数特性要求，其核函数满足二维低通特性。从时频分布的时频聚集性、交叉项抑制能力、时频分辨率和噪声抑制能力等综合指标来看，相对其他的二次时频分布，MBD 分布性能最优。

2 形态学的时频图像处理

信号的时频分布可以看作是一幅二维图像，因而可以采用图像处理方法对时频图像做进一步处理。首先将时频图像转化为灰度图，图像中像素点的不同灰度值对应时频点的能量值。从时频图像中可以看出，信号的时频分布区域聚集在IF曲线周围，而噪声的时频点散布在整个时频面上。时频面上信号的自项可以看作是图像中的“对象”，而噪声和交叉项则构成了图像的“背景”。本文从图像处理角度对信号的时频表示结果进行处理，实际上就是在灰度图像中去除背景而保留对象的过程。

各个信号的时频图像灰度值的动态范围是不一样的，为了减少数据间的不平衡性，首先对时频图像灰度值进行归一化，然后使用自适应维纳滤波器去除时频图像的噪声点，对图像进行增强。从时频图中可以看出，并非所有区域都分布有信号，对此可以检测分析信号的起止频率，将没有信号分布的图像区域剪切掉［8］，减小冗余信息，更有利于下一步对时频图像的分析。接着本文对时频图像依次进行二值化、形态学处理和标注连接分量，最终得到信号的IF估计。

2.1 时频图像二值化

时频图像二值化实际上是对图像进行阈值处理，将图像上的灰度值置为0或1，将256个亮度等级的灰度图像通过适当的阈值选取转化为仍然可以反映图像整体和局部特征二值图像，同时也减少后期图像处理的计算量和存储空间，图像的二值化处理可以描述如下：

选择合理的阈值Thr是时频图像二值化的关键，对时频图像二值化时，应尽量保留信号在时频图中对应的像素点，并尽可能去除噪声。本文阈值选取参照文献［9］中方法。

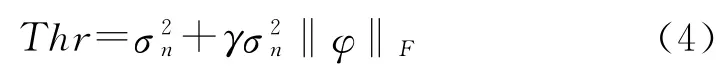
2.2 时频图像形态学处理

时频图像进行二值化后，信号分量被进一步展宽，本文进一步采用数学形态学方法消除时频面上的噪声，细化信号分量，最终估计出信号的IF。形态学处理是应用具有一定形态的结构元素对集合进行腐蚀和膨胀的操作，膨胀使时频图连通域扩张，腐蚀使时频图连通域收缩。开运算先腐蚀再膨胀，用于滤除图像中区域小于结构元素的时频独立点或明显区别于信号分量的斑点，而保留相应时频聚集面积大于结构元素的时频点，从而使信号在时频分布平面对应的自分量的轮廓变得光滑，消除时频分布平面上少量噪声对应的细的突出物，经形态学开操作处理后的二值图像可表示为：

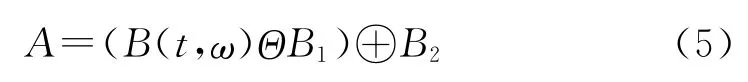
式中，B1和B2分别为腐蚀和膨胀的结构元素，Θ 表示腐蚀运算，⊕表示膨胀运算。本文中B1选择半径为5的圆盘型结构元素，B2择半径为3的菱型结构元素。

形态学骨骼化可以把二值图像区域缩成单像素的线条，以逼近区域的中心线，提取骨架的目的是减少图像成分，只留下时频图像最基本信息，要求最大限度地细化原图形，并且要求原图像中属于同一连通域的像素不出现断裂。本文通过对时频图像骨骼化，找出时频能量脊线，由于时频能量沿着IF 曲线方向聚集，因而时频能量脊线和IF曲线方向是一致的。图像A 的骨骼化表示如下：

式中，Sk（A）为骨骼子集，（AΘkB）表示对A 连续腐蚀k 次，。表示开运算。时频图像骨骼化后会出现许多毛刺，对此可以采用去毛刺算法［10］，平滑所得到的时频脊线。

2.3 IF估计

二值时频图像是由以前景像素为基本单位组成的若干个连接分量构成的，因此找出信号项对应的时频图像上的连接分量，即可确定信号的IF。而对于像素点元素比较少的连接分量可以认为是噪声，可以通过统计各连接分量像素点的个数，剔除噪声分量。对此文中采用标注连接分量方法［11］得到信号的连接分量，统计连接分量前景像素点的行索引和列索引，即可估计出信号的IF。当信号中存在多个分量时，采用连接分量标记算法同样可以区分出各个信号分量。图2中以LFM 信号（SNR＝-3dB）为例，说明了本文中时频图像的处理流程，由左至右分别是信号的时频图、经剪切后时频灰度图、二值化时频图、开运算后的时频图、骨骼化后时频图以及去毛刺后的时频图。

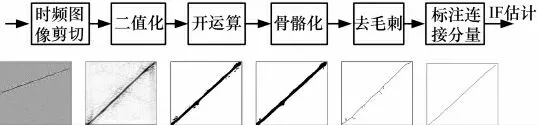
图2 时频图像处理流程

3 仿真实验

本节通过Matlab仿真对本文IF估计方法性能进行验证。实验中分别生成LFM（线性调频）、SFM（正弦频率调制）、BFSK（二进制频移键控）和EQFM（偶二次调频）四种信号。其中LFM 信号载频设为25MHz，SFM 载 频 设 为15MHz，BFSK 上 边 频 为10MHz、下边频为20MHz，EQFM 载频设为10MHz，采样频率均为200MHz，脉冲宽度为11μs，为了简化分析和计算，信号幅度设为1，仿真时噪声采用高斯白噪声。时频分布窗函数采用改进的B 分布函数，核函数参数β取为0.05，时频窗长设为161。

首先采用所提出方法分别对LFM、BFSK 和EQFM 信号的IF进行估计，信噪比为-3dB。图3（a）为LFM 信号的IF估计曲线，可以看出IF估计曲线比较平滑，较为准确地描述了信号真实的IF 变化规律；图3（b）为FSK 信号的IF 估计曲线，同样得到了该信号的有效估计，表明本文IF估计方法适用于频率突变信号；图3（c）为EQFM 信号的估计曲线，由于该信号的时频能量主要聚集在IF曲线波谷处，信号两端能量分布较少，因而在信号两端的IF 估计会出现偏差，但总体上来看其IF估计值是较为准确的。

图3 本文方法的IF估计曲线（SNR＝-3dB）

进一步将所提出方法同WVD 峰值检测法［4］以及时频分布一阶矩法［6］的IF估计效果进行比较。信噪比变化范围为-9～15dB，分别对三种IF 估计方法做500次Monte-Carlo实验。CRLB为正弦频率调制信号IF估计的克拉美罗界。表1对SFM 信号IF估计的MSE 随信噪比变化情况进行了统计。总的来说，时频分布一阶矩法的估计性能最差，在无噪声的信号环境下，采用时频分布一阶矩可得到无偏估计，但当信号中有噪声干扰时，该方法的估计性能急剧下降；当SNR≥6dB时，WVD 峰值检测法和本文方法的MSE 都接近克拉美罗界，而当SNR≤3dB 时，本文方法明显优于WVD 峰值检测法，表明本文方法在较低信噪比的IF估计性能要优于其它两种方法。从统计特性上来看，本文方法的估计性能有一定程度的提升。

表1 瞬时频率估计性能统计 （dB）

图5 多分量信号的IF估计方法比较（SNR＝-3dB）

图4为SNR＝-3dB时单分量信号的IF 估计效果图，由图中可以看出，时频分布一阶矩法得到的IF估计和真实IF曲线明显差别最大；WVD 峰值检测法得到的IF估计曲线也不是很理想，受噪声的影响，许多信号时频分布的峰值点远离IF曲线，产生了许多突变点；本文方法得到的IF曲线与真实的IF比较接近，表明采用图像处理方法能有效降低噪声对信号IF 估计的影响。图5为SNR＝-3dB 时多分量信号的IF估计效果图，由图中可以看出，传统的时频分布一阶矩和WVD 峰值法将会失效，而本文方法仍能得到有效的IF估计，主要是因为采用图像处理中的标注连接分量方法可以有效区分出时频面上的各个信号分量，所以本文方法也适用于多分量信号的IF 估计。实验结果验证了本文方法的有效性。

4 结束语

本文提出了一种将时频分析和图像处理相结合的雷达信号IF 估计方法，将时频分布转化为二值图像后，采用图像处理中的形态学方法估计出信号的IF，实验结果表明该方法在较低信噪比条件下能够获得质量较好的瞬时频率曲线，适用于多分量调频信号的IF估计。随着信噪比的降低，许多信号处理中的IF估计方法效果会变得很差，而采用图像处理方法能有效降低噪声对估计性能的影响。IF包含了丰富的信号调制信息，因此本文的研究内容对于雷达信号参数估计和调制方式识别具有较为重要的参考价值。■

［1］刘潮，李政杰，童宁宁.改进的相位建模法在瞬时频率估计中的应用［J］.航天电子对抗，2011，27（3）：23-25.

［2］Orovic′I，Stankovic′S，Thayaparan T，et al.Multiwindow S-method for instantaneous frequency estimation and its application in radar signal analysis［J］.IET Signal Processing，2010，4（4）：363-370.

［3］Khan NA，Taj IA，Jaffri M.Instantaneous frequency estimation using fractional Fourier transform and Wigner distribution［C］∥Bangalore：ICSAP’10 International Conference on Signal Acquisition and Processing，2010：319-321.

［4］Chen Guanghua，Ma Shiwei，Liu Ming，et al.Wigner-Ville distribution and cross Wigner-Ville distribution of noisy signals［J］.Journal of Systems Engineering and Electronics，2008，19（5）：1053-1057.

［5］Lerga J，Sucic V.Nonlinear IF estimation based on the pseudo WVD adapted using the improved sliding pairwise ICI rule［J］.IEEE Signal Processing Letters，2009，16（11）：953-956.

［6］Baraniuk RG，Coates M，Steeghs P.Hybrid linear／quadratic time–frequency attributes［J］.IEEE Trans.Signal Processing，2001，49（4）：760-766.

［7］Hussain Z，Boashash B.Adaptive instantaneous frequency estimation of multi-component FM signals using quadratic time frequency distributions［J］.IEEE Trans.Signal Processing，2002，50（8）：1866-1876.

［8］Zilberman ER，Pace PE.Autonomous time-frequency morphological feature extraction algorithm for LPI radar modulation classification［C］∥Atlanta，GA：Proc.of the IEEE International Conference on Image Processing，2006：2321-2324.

［9］尚海燕，水鹏朗，张守宏，等.基于时频形态学滤波的能量积累 检 测［J］.电 子 与 信 息 学 报，2007，29（6）：1416-1420.

［10］Gonzalez RC，Woods RE，Eddins SL.Digital image processing using MATLAB［M］.2nd ed.Gatemark Publishing，Inc.，2009.

［11］Lagrange M，Marchand S.Estimating the instantaneous frequency of sinusoidal components using phase-based methods［J］.Journal of the Audio Engineering Society，2007，1（55）：385-399.