基于线性阵列的纱线直径与毛羽测量方法
袁汝旺,蒋秀明,周国庆,杜玉红
(天津工业大学天津市现代机电装备技术重点实验室,天津 300387)
纱线的外观质量直接影响纺织品的质量,可利用视觉检测技术测量纱线直径、毛羽等工艺参数,以提高产品质量和生产效率[1-3]。Guha A、Ohta K、Cybulska M和Ozkaya Y A等利用数字图像处理技术,研究纱线直径、毛羽和捻度等特征的自动识别、提取和参数估计方法[4-6],分析不同实验条件和图像处理方法对测量结果的影响[7];Carvalho V H等采用光电二极管和相干光信号处理技术开发纱线毛羽和基于平均直径的纱疵评价系统[8-10],运用快速傅里叶交换(FFT)和快速小波直方图技术(FWHT)对数字信号进行处理和频谱分析,获取纱线直径、线密度和不规则参数[11-13]。随着新型半导体集成光器件的发展,线性阵列测量技术可用于检测纱线外观直径和毛羽等工艺参数[3,14]。本文依据线性阵列测径原理,开发一种新的非接触式纱线外观质量监测系统,研究纱线直径测量和毛羽估计的方法,提出了纱线直径测量的提取算法,分析浮动阈值变化对测量结果的影响,达到纱线直径和毛羽评价目的,可为纱线生产过程监测提供一定的理论和实验参考,并有助于提高产品质量和生产效率。
1 纱线直径与毛羽测量原理
1.1 线性阵列测径原理
线性阵列是指将多个具备敏感可读区域(像素)光敏原件感测器排列在1条独立的直线上,其光敏原件感测器主要包括电荷耦合器件(CCD)和互补金属氧化物半导体晶体管(CMOS)2种形式。Koganeya K、Millman M P和Carvalho V H等利用线性阵列CCD/CMOS视觉检测技术开发纱线外观质量检测及评级系统,研究纱线直径、毛羽、棉结等工艺参数的测量原理及方法,提出了纱线核直径的概念和提取算法,实现工艺参数自动准确测量;但是系统复杂,数据处理计算工作量大,实时测量存在欠缺[14-16]。线性阵列测径的工作原理如图1所示。
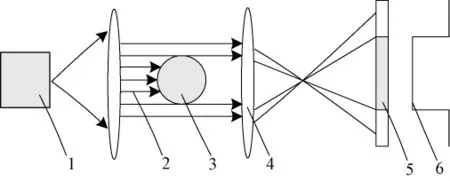
图1 线性阵列测量原理Fig.1 Measuring principle of linear array
通过光学系统将纱线直径尺寸以一定的、准确的倍率成像于线性阵列光敏面上,对线性阵列输出信号进行A/D转换,送往计算机,实现相应的测量,式(1)给出了纱线直径测量的基本模型[17]。

式中:d为纱线径值,mm;h为线性阵列像素宽度,mm;△P为纱线直径所遮挡的线阵像素个数;β为光学系统放大倍数。
1.2 纱线毛羽估计
图2示出纱线外观结构。沿纱线轴向任意位置做垂直线ab,线性阵列测量所获得的纱线直径主要由纱线核直径(ab部分)和毛羽(ab外侧突出部分)构成,采用线性阵列测量纱线直径时,纱线直径的大小与线阵元件的输出电压成比例关系,毛羽影响线性阵列的电压输出信号,而纱线核直径取决于ab之间的线阵像素个数,因此,纱线毛羽率的估计原理如式(2)所示。
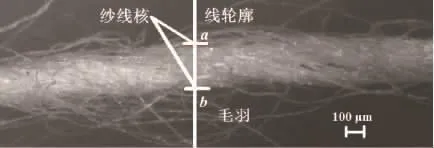
图2 纱线外观结构Fig.2 Structure of yarn appearance
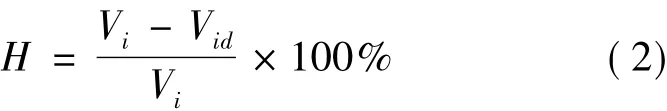
式中:H为纱线核之外的毛羽投影和纱线投影的比值,即毛羽率,%;Vi为纱线直径输出电压,V;Vid为纱线核直径计算输出电压,V。
2 纱线核直径提取算法
2.1 线轮廓特征信号递归平均滤波原理
图3描述了纱线在直线ab位置线轮廓特征像素与密度的关系,纱线核直径为线轮廓特征的最深轮廓线与浮动阈值交叉点a、b之间的宽度,其中D表示接收光线的明暗程度。
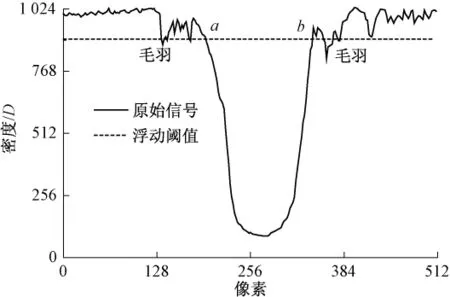
图3 纱线直径线轮廓特征曲线Fig.3 Characteristic curve of line profile on yarn diameter
从图3中可知浮动阈值变化影响纱线直径的测量结果,因此,本文提出一种递归平均滤波的方法对线轮廓特征信号进行平滑处理,其基本思想是判断测量范围内任意像素所对应的线轮廓特征信号瞬时密度值与平均密度值的大小,确定其保持不变或用饱和阈值替代,式(3)、(4)给出了基本原理。
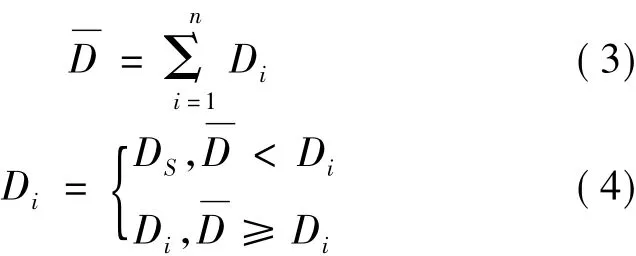
式中:Di为瞬时密度值;为平均密度测值;DS为饱和阈值,n为采样个数。
2.2 纱线核直径像素坐标提取
假定线轮廓特征曲线的最深轮廓线与浮动阈值交叉点a和b,且所对应的像素坐标分别为PL和PR。因为最深轮廓线两侧均具有单调性,且像素坐标PL(或PR)∈[Pi,Pi+1],i=0,1,…,N- 1,所以当(DF-Di)(DF-Di+1)≤0时,采用线性插值自动获取像素坐标PL和PR,式(5)给出了像素坐标的提取算法。
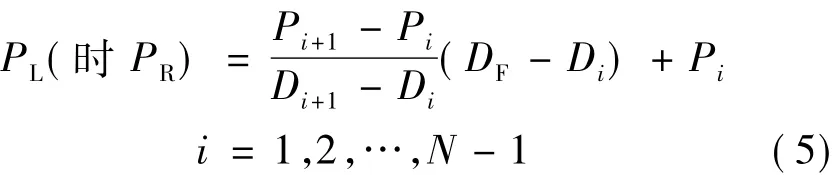
式中:DF为浮动阈值;Pi为像素坐标。
首先是用典修辞格的使用。“水向东流”是李煜“问君能有几多愁,恰似一江春水向东流”典故的使用,表现了主任公内心无限的愁苦。
2.3 算法的实现
利用递归平均滤波和线性插值像素坐标提取实现纱线直径测量的具体步骤如下:
1)设定饱和阈值DS、浮动阈值DF和线阵最大像素值n;
2)获取没有纱线通过时的噪声干扰信号Dc和纱线直径测量信号Di,并计算Di=Di-Dc
3)利用式(3)、(4)对直径信号进行滤波处理,计算纱线直径测量信号的平均值,将瞬时密度值大于平均密度的信号用饱和阈值DS代替;
4)利用步骤3的结果,重复步骤3的流程,对非饱和阈值信号处理;
5)判断所在像素区间,确定最深轮廓线和饱和阈值交叉点的像素坐标,利用式(5)计算所对应的像素值PL、PR;
6)利用步骤5的结果,确定最深轮廓线和饱和阈值交叉点之间的像素个数△P=PR-PL,并根据式(1)计算纱线直径d。
3 实验结果与分析
3.1 实验条件
纱线直径测量系统主要由智能激光传感器(激光光源、光学系统、线阵接收单元)、测量流程控制与数据分析系统、样本喂入速度控制系统和张力控制系统组成,表1给出了测量系统的主要技术参数指标。
实验研究的样本选用36.9 tex棉纱线,光学系统放大倍数β=1系统硬件的对测量信号的采样周期为1 ms,采样时间间隔为10 ms,张力T=50 mN,喂入速度v=12 m/min。
为了验证测量系统的稳定性和测量结果再现性选,用直径为2、1、0.5、0.1 mm 4种不同规格的铜丝对测量系统进行校准,确定纱线直径信号与输出电压的物理关系,图4示出测量系统的线性关系。校准结果表明,测量系统具有良好的线性关系[18]。

表1 线阵激光传感器参数Tab.1 Param eters of linear array laser sensor
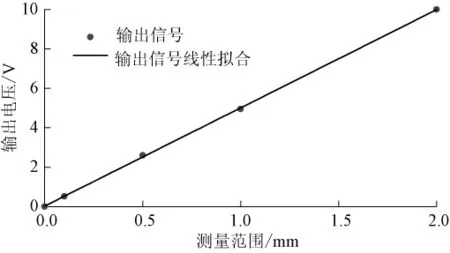
图4 测量系统的线性关系Fig.4 Linear relationship ofmeasuring system
3.2 实验结果与讨论
3.2.1 递归平均滤波算法仿真与分析
设定信号处理的饱和阈值为1 024,浮动阈值为768。图5示出纱线直径线轮廓特征信号递归平均滤波过程。图5(a)示出线轮廓特征的原始测量信号,其非饱和阈值信号平均密度值=901.53,最深轮廓线说明了纱线核直径的轮廓边界,在最深轮廓线两侧主要为纱线毛羽,浮动阈值与线轮廓特征信号曲线的交点为C、D、E、F,其中纱线核直径为交叉点C、D之间的宽度,交叉点E、F之间的宽度为毛羽信号;图5(b)给出第1次递归平均滤波后的结果,其非饱和阈值信号平均密度值=484.06,部分噪声信号和毛羽信号被滤除,浮动阈值与信号曲线的交点不变,影响核直径的毛羽信号仍然存在;图5(c)给出第2次递归平均滤波后的结果,其非饱和阈值信号平均密度值=166.49,噪声和毛羽信号被全部滤除,交叉点C、D之间的宽度为有效的纱线核直径。结果表明经过2次递归平均滤波处理后,影响纱线直径测量的毛羽和噪声信号被全部滤除,能够有效测量纱线直径。
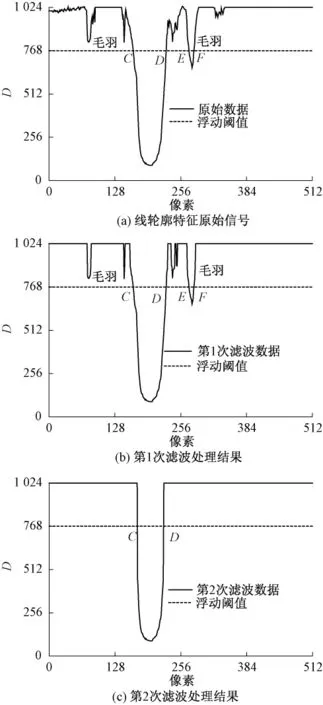
图5 递归平均滤波处理算法Fig.5 Algorithm of filtering process on recursive averaging.(a)Initial signal of line profile characteristic;(b)Results of first filtering processing;(c)Results of second filtering processing
为分析在递归平均滤波处理过程中阈值变化对测量结果的影响,选取3种不同的浮动阈值分别为512、768和1 000,表2示出滤波处理过程中浮动阈值与最深轮廓线交叉点C、D所对应的像素坐标和直径像素变化情况。从表中可看出,在递归平均滤波处理过程中,浮动阈值变化对原始信号确定的纱线直径影响最大,直径像素误差为53,而对第2次滤波处理后确定的纱线直径影响最小,直径像素误差为2。在信号处理过程中,当选取浮动阈值为512,直径像素变化最小,误差为2;当选取浮动阈值为1 000,直径像素变化最大,误差为53。结果表明当浮动阈值接近于饱和阈值时,受噪声、毛羽等高频信号的影响,直径测量结果误差大;当浮动阈值为饱和阈值的50%时,测量结果变化小。
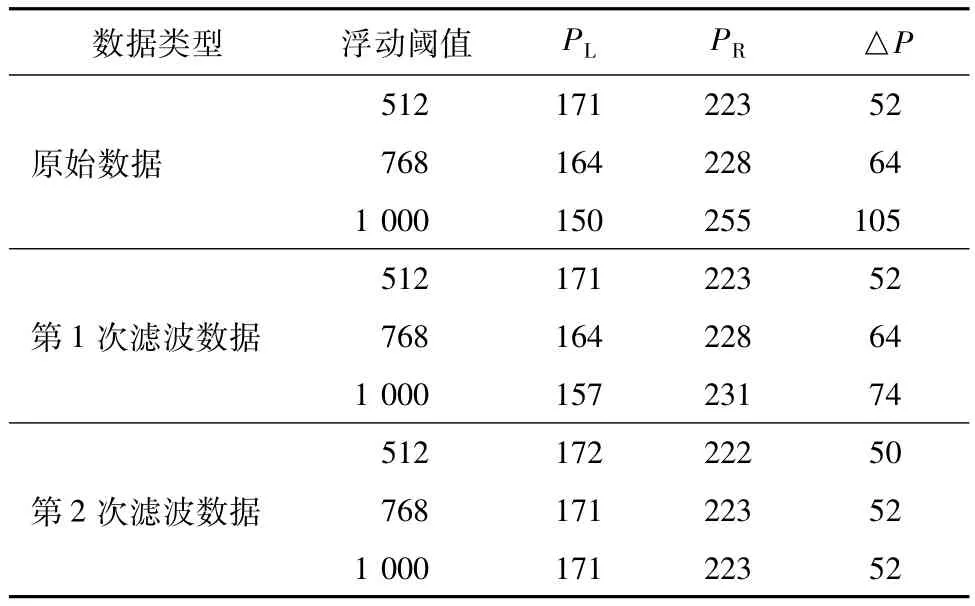
表2 不同阈值的直径像素Tab.2 Pixels of diameter w ith different thresholds
3.2.2 纱线直径测量和毛羽率估计结果与讨论
测量系统输出结果不失真的条件是纱线样本不规则的最小波长为线阵接收单元宽度的10倍[18],因此,利用测量系统获取100个采样点作为样本片段,其中每10个采样点为1个子片段,共10个子片段。图6示出采样过程中直径像素变化情况。样本片段的直径像素平均值为 53.2,变异系数为12.8%。
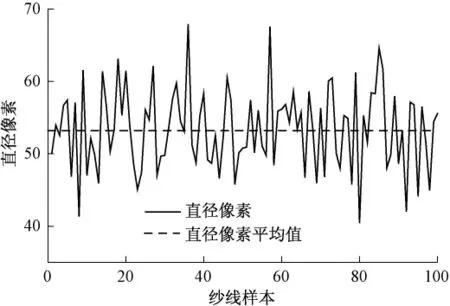
图6 纱线直径测量信号Fig.6 Measured signal of yarn diameter
表3示出利用递归平均算法滤波处理后获得的样本子片段纱线直径测量与毛羽率估计的结果。纱线样本的平均直径为0.213 mm,毛羽率估计平均值为6.50%。
图7示出子片段直径与毛羽率变化情况,从中可看出子片段纱线直径和毛羽率估计值的变化情况。纱线平均直径变化范围是[-4.23%,5.16%],标准差为3.40%。纱线样本子片段直径条干均匀,对片段不规则影响小。纱线平均毛羽率变化范围是[-33.38%,30.25%],标准差为23.56%。纱线样本子片段毛羽率变化大,加剧片段不规则。
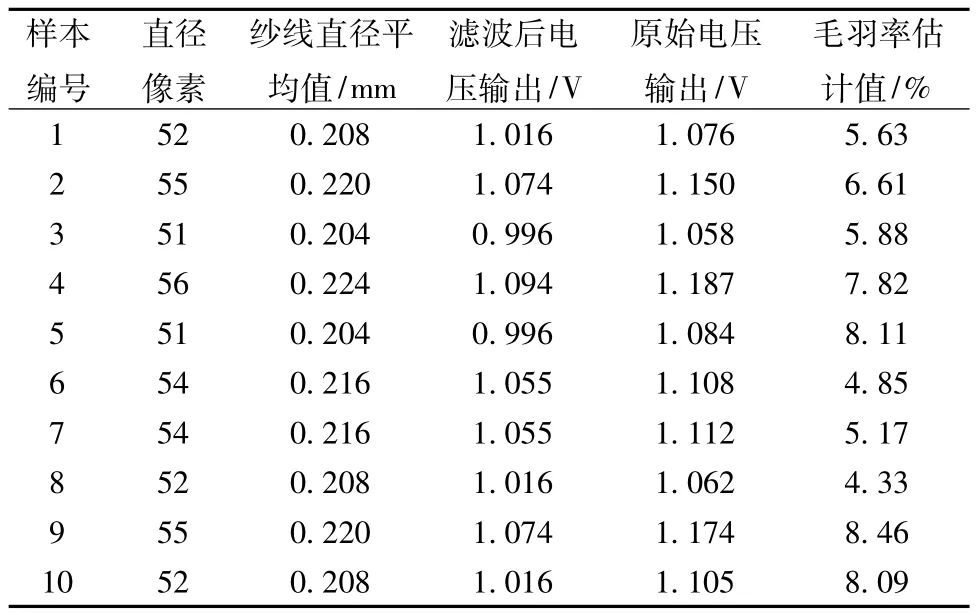
表3 样本子片段直径测量与毛羽率估计结果Tab.3 Results on measurement of diameter and estimation of hairiness rate for sam p le sub-segment
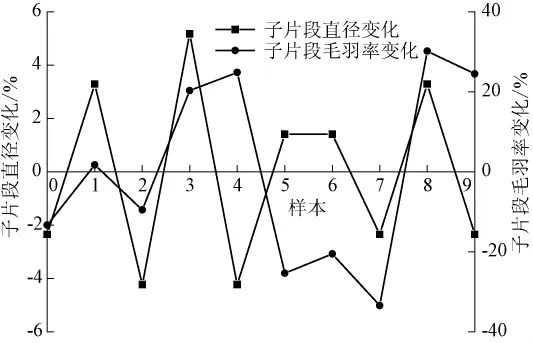
图7 子片段直径与毛羽变化Fig.7 Variation on diameter and hairiness of subsegment
4 结论
1)基于线性阵列测量技术,利用线阵CCD激光传感器开发的非接触式测量系统能够实时测量纱线直径和毛羽,且测量系统精度和灵敏度高,数据结果可靠。
2)针对高频噪声和毛羽信号,对纱线直径线轮廓特征信号进行2次递归平均滤波处理后,可获得精确地纱线直径像素,准确测量纱线直径和估计纱线毛羽率。
3)利用线性插值方法自动获得浮动阈值与线轮廓特征信号交叉点的像素坐标,且不同浮动阈值影响递归平均滤波处理过程中的直径像素,浮动阈值越接近饱和阈值,对直径像素影响越大,测量结果准确性就越差。characterizati on system:design of a prototype[J].Sensors Journal,IEEE,2009,9(8):987-993.
[1] CARVALHO Vitor H, BELSLEY Michael S,VASCONCELOS Rosa M,et al.Automatic yarn
[2] CARVALHO V,CARDOSO P,BELSLEY M,et al.Development of a yarn evenness measurement and hairiness analysis system[C]//CAPOLINO Gerard Andre. 32nd Annual Conference on Industrial Electronics.Paris:Industrial Electronics Society of IEEE,2006:3621 -3626.
[3] TRESANCHEZM,PALLEJÀ T,TEIXIDÓ M,et al.Measuring yarn diameter using inexpensive optical sensors[J].Procedia Engineering,2010,5:236 -239.
[4] GUHA Anirban,AMARNATH C,PATERIA S,et al.Measurement of yarn hairiness by digital image processing[J].Journal of the Textile Institute,2009,101(3):214-222.
[5] OHTA Ken'ichi,HATA Yutaka,OHTA Chikako,etal.Measuring the appearance diameter of yarns using visual information[J].Sen'i Gakkaishi,2000,56(11):518-523.
[6] OZKAYA Y A,ACAR M,JACKSON M R.Yarn twist measurement using digital imaging[J].Journal of the Textile Institute,2008,101(2):91-100.
[7] CYBULSKA Maria.Assessing yarn structure with image analysismethods1[J].Textile Research Journal,1999,69(5):369-373.
[8] CARVALHO Vítor H, CARDOSO Paulo J,VASCONCELOSRosa M,et al.Optical Yarn hairiness measurement system [C]//DIETRICH Dietmar,HANCKE Gerhard.5th International Conference on Industrial Informatics.Vienna:Industrial Electronics Society of IEEE,2007:359-364.
[9] CARVALHO Vítor H,CARDOSO Paulo J,BELSLEY Michael S,et al.Yarn hairiness characterization using two orthogonal directions [J].Instrumentation and Measurement,2009,58(3):594 -601.
[10] CARVALHO Vítor H,CARDOSO Paulo J,BELSLEY Michael S,et al.Yarn diameter measurements using coherent optical signal processing[J].Sensors Journal,IEEE,2008,8(11):1785-1793.
[11] CARVALHO Vítor, MONTEIRO Joāo L, SOARES Filomena O,et al. Yarn evenness parameters evaluation:a new approach[J].Textile Research Journal,2008,78(2):119 -127.
[12] CARVALHO V,SOARES F,BELSLEY M,et al.Automatic yarn characterization system [C]//BONFIGLIO Silvio,BEKIARIS Angelos ROLLER Dagmar.IEEE Sensors 2008.Lecce,IEEE Sensors,2008:780-783.
[13] TÀPIASMontserrat,RALLÓ Miquel,ESCOFET Jaume.Automatic measurements of partial cover factors and yarn diameters in fabrics using image processing[J].Textile Research Journal,2011,81(2):173 -186.
[14] CARVALHO Vítor, BELSLEY Michael,VASCONCELOS Rosa M,et al.Yarn hairiness and diameter characterization using a CMOS line array[J].Measurement,2008,41(10):1077 -1092.
[15] MILLMAN M P,ACAR M,JACKSON M R.Computer vision for textured yarn interlace(nip)measurements at high speeds[J].Mechatronics,2001,11(8):1025 -1038.
[16] KOGANEYA Keizo,YUKISHITA Youichi,FUJISAKI Hirotaka,et al. Instrument for measuring the appearance width of running double ply staple yarn using lightness threshold for yarn image[J].Sen-IGakkaishi,2012,68(4):98-105.
[17] 苏波,王纪龙,王云才.CCD高精度测径系统的研究[J].太原理工大学学报,2002,33(5):506-509.SU Bo,WANG Jilong,WANG Yuncai.Research on high accuracy diametermeasur ement system with CCD[J].Journal of Taiyuan University of Technology,2002,33(5):506-509.
[18] 袁汝旺,蒋秀明,杨公源.纤维束条干外观不匀的激光测量方法[J].中国激光,2012,39(7):176-180.YUAN Ruwang,JIANG Xiuming,YANG Gongyuan.Measuring method for appearance unevenness of fiber bundles[J].Chinese Journal of Lasers,2012,39(7):176-180.

