可视化教学与团队研讨式学习模式探索
胡金杰 陈志祥
(绍兴文理学院 数学系,浙江 绍兴312000)
0 引言
理论教学是大学生数学课程的主要教学方式,大量引理和定理的抽象推导与证明过程是大学数学的主流教学模式.由于近些年来的扩招等因素,普通大学的大学生对学习数学的畏惧心逐渐加重,学习数学的兴趣普遍下降.然而,数学被广泛而深入地应用于不同的领域,包括科学、工程、医学和经济学等,特别是以解决复杂实际问题著称的应用数学,越来越被重视.在新的形势下,高等学校提出了大力加强学生实践能力培养的总体方向,给数学教学提出了新的挑战,同时也是一个难得的机遇.如何切实提高数学教学的实践性、创新性就显得格外重要.
数学模型课程是一门综合性强、实践要求高、与社会实际问题紧密联系的应用型课程.改革的目标是以“用数学”为宗旨,以可视化教学为主要教学途径,实施“问题驱动”的研讨式学习模式.整体过程大致可描述为:把每套案例看成一个具体的实际问题,作为一个学习单元,学生团队协作,边学边查边用,从基础理论学习到结果输出及应用推广,并形成一个小系统,最后撰写出一篇小论文.本教学改革大力度地改变了传统的教师讲授为主、学生单独被动接受知识的局面,在多方面体现出改革的显著成效.
1 可视化的概念
要把复杂而抽象的数学问题阐述清楚,便于数学专业学生和非数学专业学生的理解,引入图形、图像和序列图形是一种不错的选择.可视化教学是系统化利用图形图像辅助教学的新型教学手段,在国外已有较系统研究,在国内,可视化教学虽然还有待完善,但在数学模型建立过程中,特别是数据处理、求解过程及结果分析中,化抽象为形象的可视化技术能起到显著的教学效果.
可视化(Visualization)是利用计算机图形学和图像处理技术,将数据转换成图形或图像在屏幕上显示出来,并进行交互处理的理论、方法和技术[1].可视化应用领域广泛,在数学领域上的应用较多的是科学计算可视化,最常见的是用多幅图形来表现二维或三维复杂曲线曲面的特征,把计算的结果用图形直观地表现出来[2].另一方面的重要用途是把离散的杂乱数据用散点图等方式描述出来,让研究者可以更直观地寻找数据内部可能存在的规律性.可视化技术已成为研究数据表示、数据处理、决策分析和结果分析等一系列问题的综合技术[3],本文引入的可视化技术主要是其中的科学计算可视化.
科学计算可视化[1,4]是美国国家科学基金会在1987年的一份报告中正式提出的,科学计算可视化的基本含义是运用计算机图形学或者一般图形学的原理和方法,将科学与工程计算等产生的大规模数据转换为图形、图像,以直观的形式表示出来.科学计算可视化在教学中的应用,已有些学者作了探索和实践[5-10],本文把科学计算可视化引入到教学中,主要在数据分析和处理过程、数学模型的数值求解过程、模型结果的分析检验过程中得到体现.具体做法:
(1)做详细的数据分析处理,在多媒体课堂上从多角度展现数据的离散特征.从数据特征结合机理分析,推演模型的建立过程.
(2)对优化过程、微分方程数值求解过程、网络学习过程等复杂的过程,给出中间过程的序列图形,弥补理论教学中无法直接展现的弊病.
(3)对优化结果、方程的数值解和网络学习的泛化效果等进行图表分析,进一步分析模型与实际问题的吻合程度.
2 教学模式框架的构建
2.1 理论教学环节
对于每一套案例,理论教学环节是教学的基础和先导,为了培养学生理解、分析和解决实际问题的能力,在讲授时,需要详细引入问题的背景,穿插该问题的更一般性、往往也是更复杂化的“一类”社会实际问题.这个环节主要分为以下三个部分.
2.1.1 案例的选取
由于整个教学课时有限,数学模型课程一般选取8到10个主讲案例[11],每个主案例都配上一个指定的辅助案例,由学生自学完成.案例的选择依据主要是数学模型各知识点中的典型实例,并充分考虑知识点覆盖面和模型的复杂程度.
2.1.2 可视化辅助问题分析和数据处理
从教材中遴选的大部分案例,是源自社会实际问题,教材对这些问题往往作了简化,特别是其数据,不但量少,且往往已被处理成理想化的数据.在进行问题分析时,要一定程度的回归实际问题的原型,适当扩大样本数据的规模和复杂性.同时,源于实际问题的数据内往往蕴含着某些规律性,数据处理的一个重要任务是刻画出这些潜在的规律性.在理论课堂上需要做好两方面教学工作:
(1)在合适的假设下,进行严格的理论推演,也即机理分析.抓住问题的内在联系,进行深入的机理分析.因为机理分析具有较强的理论推演,对于非数学专业的学生来说,课堂理解上存在较大困难,需要运用可视化手段来辅助教学.
(2)绘制样本数据的散点图.为了探究样本数据可能表现出来的特征,基于合理的假设,选取若干量之间的关系,绘制散点图.对于大部分案例,绘制散点图是非常有必要的.比如,在讲授“牙膏的销售”案例[11]中,为了了解销售量与售价、差价、广告费等究竟是什么样的关系,可以把销售量作为因变量,选其他一种或两种量作为自变量,绘制多幅静态的散点图,来研究数据内在可能存在的大致函数关系.本环节利用Matlab软件实现图形展示并作深入分析.
2.1.3 模型的建立过程
本环节是理论课主讲的中心内容.与教学模式改革前相比,模型建立过程的讲授得到了明显加强,其他诸如知识点的理论证明、模型求解的各种方法介绍等,由于理论要求过高,适当降低了要求,在实践环节中则充分强调怎么编程实现.为了把较抽象的模型建立过程讲透,一方面需要引导学生查找学术文献,并要在小论文中得到充分体现,另一方面要求学生在合理的分析过程中,借助已学的各种知识和参考相关专业知识一步步地进行推演,每个公式都要有根有据.我们在强调“用数学”的同时,不能丢掉数学的严密的逻辑性.
2.2 实践教学环节
学生以3人一组形式进行上机实践,实验教学环节要解决下列问题:
(1)每组至少1位学生负责搜索文献、阅读文献,以寻求更好的模型参考.
(2)另两位学生编程以求解模型,编程绘制序列图以展示模型求解的中间过程.
(3)用图形、表格和相应文字来展示模型求解的结果,作比较、检验及参数灵敏性分析等,并作撰写小论文的准备.
实践环节中,教师的示范操作非常关键,示范操作的重点在于编程、中间过程图形展示和结果分析等方面.教师要引导学生完成文献查阅和编程,解决学生在上机实践中遇到的各种问题,使学生能在实践课堂内完成主体程序,构建整个小论文的框架,并在课外完成模型的具体求解.实践教学环节是教学模式改革的一个重要环节,重点强化图形化过程,把科学计算可视化充分运用到实践环节中.
2.3 学习团队研讨环节
关于团队学习的概念及其重要性,最先提出的学者是国际组织学习协会的创始人彼得圣吉(Peter M.Senge),在他的《第五项修炼:学习型组织的艺术和实践》中阐述了团队学习的概念[12-13],即团队学习是发展团队成员整体搭配与实现共同目标的能力的过程,它建立在发展共同意愿和自我超越的基础之上.我们也可理解为,团队学习是个体学习和协作学习的整合与升华,它可以发挥团队成员的集体智慧,使学习转换为现实的创造力[14].
陈国权[13]提出了组织团队学习的九种行为和相应的组织学习的九种能力:发现能力、发明能力、选择能力、执行能力、推广能力、反思能力、获取知识能力、输出知识能力和建立知识库能力.在本课程提倡的学生学习团队研讨过程中,这九种能力都在一定程度上得到锻炼,特别是选择能力、执行能力、推广能力、反思能力、知识的获取和输出能力得到显著锻炼.
学习团队建设[15]是本课程教改的关键点.由教师指定好要进行研讨的案例,规定好每次研讨的重点和拓展点,并选好团队的队长.实际执行时,共研讨了5套案例的小论文.
2.3.1 学习团队研讨的具体实施方案
(1)全班以3人为一个小组,4个小组为一个大组组成3个大组.每小组设一个小组长,每个大组由一个班委来当大组长.
(2)研讨时,每个大组在不同教室独立开讨论课,由大组长主持,每组由小组长安排该组同学上讲台陈述本组的论文主要内容、模型结果和图形展示.下面各组至少提出一个问题,由陈述者回答.大组长还负责在讨论情况记录纸上记录各组陈述情况和回答问题情况.
(3)教师随机旁听,并就研讨中出现的问题进行适当干预,及时纠正,同时作好讨论情况的记录工作.
2.3.2 学习团队研讨所取得的效果分析
在研讨活动准备阶段,学生先查阅相当数量的文献,理解、吸收并进行适当转化后,运用到自己的案例学习中来.在汲取他人相关知识的过程中,慢慢形成自己的新想法新观点,这使得提出有创新意义的新模型成为可能.此过程有利于学生获取并积累新知识,逐步形成知识链,成为更好解决问题的理论基础.
在学生上讲台陈述自己的解题思路、观点、方法和结果的过程中,非常高效地锻炼了学生的表达能力和知识输出能力,也锻炼了其胆魄.在实践中,学生经历了从开始时不愿上讲台,到跃跃欲试,到最后争着上讲台的蜕变过程.在第三次研讨活动时,教师修改了研讨规则,由原来每组至少讲述8分钟,改为每组至多讲述20分钟.
虽然学习团队研讨活动是放在课堂外进行,不占用正常上课时间,学生们依然非常自觉,没有抵触情绪.在整个过程中,只有3人次请假,无旷课记录.这是非常难得的,说明学生确实是自己有了兴趣,有了主动意识.
2.4 交叉评阅和考核环节
由于三人合作完成各个环节,难免出现个别学生不够努力,指望本组其他成员来完成小论文和讨论过程的现象.这种现象我们称其为“搭便车”现象.为有效杜绝或减少学生搭便车现象,一方面实行两组配对,结成互评小组,实行交叉评阅,并对评阅要求和评阅规范作了详细规定,在对比中找差距、找新思路,同时也起到互相监督作用;另一方面考核中实行“差异性”考核,即根据整组的各项表现情况,教师给出整组的总分,由小组长来分配给组内的三人,要求尽量体现分数差异.该措施把一部分权力下放给小组长,有利于激发团队协作性能,并收到良好效果.
本课程的整体考核为:小论文成绩占30%,学习团队研讨成绩占30%,交叉评阅成绩占10%,期末理论考试成绩占30%.
3 课改效果
相比于改革前,学生主动参与的程度大大提高.学生在完成理论课和实践课的课堂学习外,还要在课外完成撰写八篇以上符合要求的小论文,并在课外时间进行六次以上讨论课.同时,教师的压力也大大提升.教师要准备好每套案例的各个环节,及时记录讨论课情况和书写教改日志,还要批阅大量的小论文、引导学生寻求建立更好的数学模型,并建立可视化图形库.
在临近教改项目结题时,教师设计了《数学模型课程学习团队学生问卷调查表》,调查结果较好地反映出学生学习和讨论情况.简要总结如下:
(1)92%以上的学生认为,此项目对培养学生能力、提高创新意识和对学生能力要求上是有利的、积极的.82%以上的学生感觉题目偏难,小论文数量和质量要求偏高,但还能接受.
(2)28%左右的学生常常课外讨论,36%的学生小论文是组内轮流撰写完成的,47%的学生由组长分配任务写论文,50%的学生是通过上网找资料来整合论文的.
(3)11%的学生查阅大量文献,51%的学生查阅3篇以上文献,30%基本没找文献,而只有8%以复制为主.
(4)72%的学生每套案例需要花费7小时以上的时间,22%学生每套案例花费3小时左右.只有5%的学生不怎么花时间.
(5)在交叉评阅环节,约1/3的组由单人看论文进行评阅,1/3的组3人全看论文.52%的学生觉得交叉评阅有意义,而39%的学生觉得交叉评阅是种形式,9%的学生觉得交叉评阅没有用.
(6)61%的学生对上台讨论作了较好的准备,13.8%的学生基本不准备,95%的学生比较关注同学的台上讲评,但基本提不出问题或不大去想提问题.
(7)组队方面,17%感觉组队良好,58%的学生组队问题不大,25%的组队有些问题,但也还能勉强维持.
这份调查问卷比较真实地反映出了教改情况,绝大多数学生在相对高的要求下,比较认真地学习,也对此次学习团队项目给予较大的支持,极少数学生学习态度有待提高.从调查结果分析看,此项目的可行性得到了证实,效果应该比较好,学生的自主学习意识也得到较大的提高.
在新的培养方案下,因为该课程只有一个专业开设,所以未实施对比式问卷调查,以后条件允许可以先进行对比性试验,由此得到的问卷调查数据,将会更令人信服.尽管如此,但从笔者近几年授课经历看,在新的教学模式下,学生的自主学习能力、团队协作学习能力和查阅文献能力都得到显著锻炼和提高.
4 案例中科学计算可视化展示
4.1 相关性可视化
许多实际问题,都要用统计的方法来分析两个因素之间的相关性.相关性是刻画两个因素之间存在相互联系的程度,其数值称为相关度.一个简单的理解就是一个变量在多大程度上随着另一个变量的变化而变化.相关性是一个基本概念,学生一学就懂,但却很难深入理解.
利用可视化技术,可以很直观地表现两个因素之间的关联程度.图1给出了解释“相关性”概念的一系列对比图.
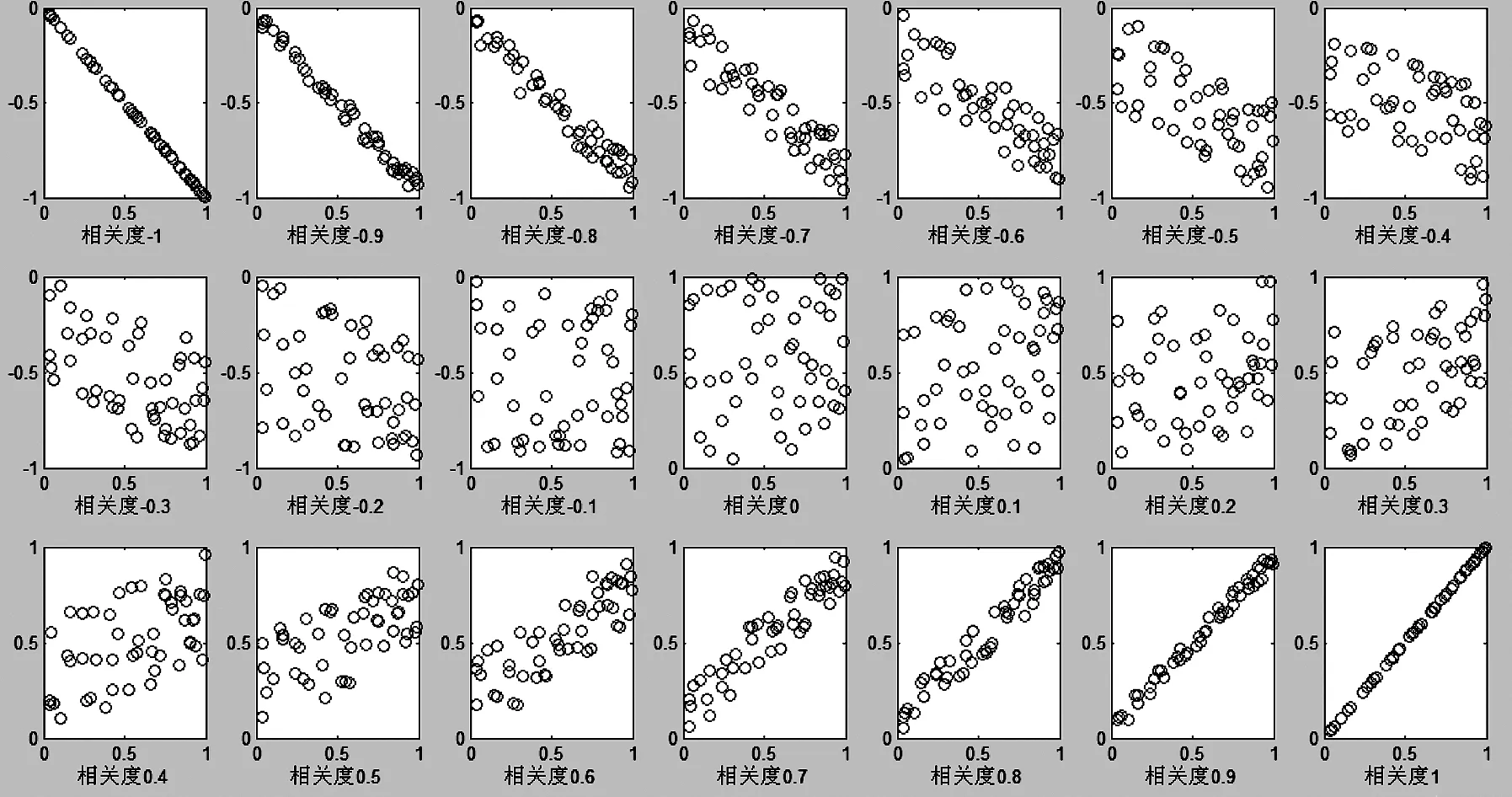
图1 解释两个因素相关度为-1到1的散点图
图1中,每个子图的两组属性X,Y都具有50个属性值,这些属性值服从均匀分布并随机产生,使得X和Y的相关度从-1到1,相邻子图的相关度相差0.1.图1中每个小圆圈代表50对属性中的一对,其x坐标是属性X的一个属性的值,y坐标是属性Y的对应属性的值.
子图下面的相关度的值用来刻画本子图中属性X与属性Y的相关性.以图1第一行最右边的“相关度-0.4”的子图为例,纵坐标(因为图较小,不宜作坐标轴标记)总体上随着横坐标的增大而变小,它们是负相关的,但关联性不是很强.相关度为-1或1的,表示两者关联性最强.第二行正中间的“关联度0”的子图,两属性呈现出完全不相关的状态.
通过类似的例子,使学生从定性理解转换为定量分析上来,从字面理解转化为具体生动的图形表现来辅助理解,大大提高学生学习数学的兴趣,加深对抽象概念的理解.
4.2 优化过程的可视化
下面再以一个非线性最优化模型为例,来看看模型求解过程的可视化.
建立的非线性整数规划模型如下:
在不考虑整数条件下,其求解结果为:x1=6.08,x2=0.41,zmin=215.50.这个结果是在不考虑整数条件下的最优解,并且可能与求解时所给的初始值有关.对于非线性规划,所得到的解有可能只是局部最优解,并且要通过严格的理论证明一个解是全局最优解是很难实现的,这是模型求解过程中经常遇到的难题.怎么才能避开严格理论证明又能准确判断一个解是否为局部最优解呢?运用可视化技术远比用文字表述来得有说服力.我们可以放宽约束来绘制曲面图,见图2.

图2 目标函数在决策变量上下界内的曲面图
从图2可以看出,在决策变量的上下界[-10,20]内,曲面的极小值点只会落在一个凹形区域内,可以直观、不严格地得出结论:上面的最优解是全局最优解.
下面我们来解决整数约束问题.观察图2,并根据目标函数的性状,可以得出,整数下的最优解应该在点(6.08,0.41)附近.显然,与此点相邻的整数点有四个点:(6,0),(6,1),(7,0),(7,1),见图3.
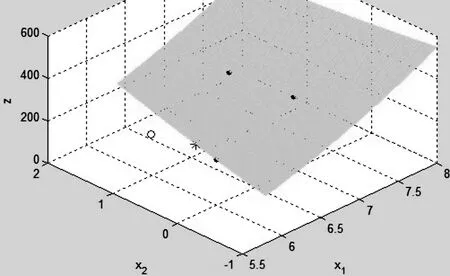
图3 整数最优解落在连续最优解的四周:视角为(-45,45)
图3是从视角(-45,45)方向看这5个点的结果.“*”标记的点为无整数条件下的连续最优解(6.08,0.41,215.50).“·”标记的3个点,为符合约束条件的3个点,分别为:(6,0,216),(7,0,343),(7,1,318),“o”标记的点为不符合约束条件的点(6,1,195).从图3中可以清楚看到,(6,0,216)恰好落在可行域的边缘.
为了让学生看得更清楚,我们可以对图形进行旋转,即调整视角,来选择较佳的观察角度,见图4.
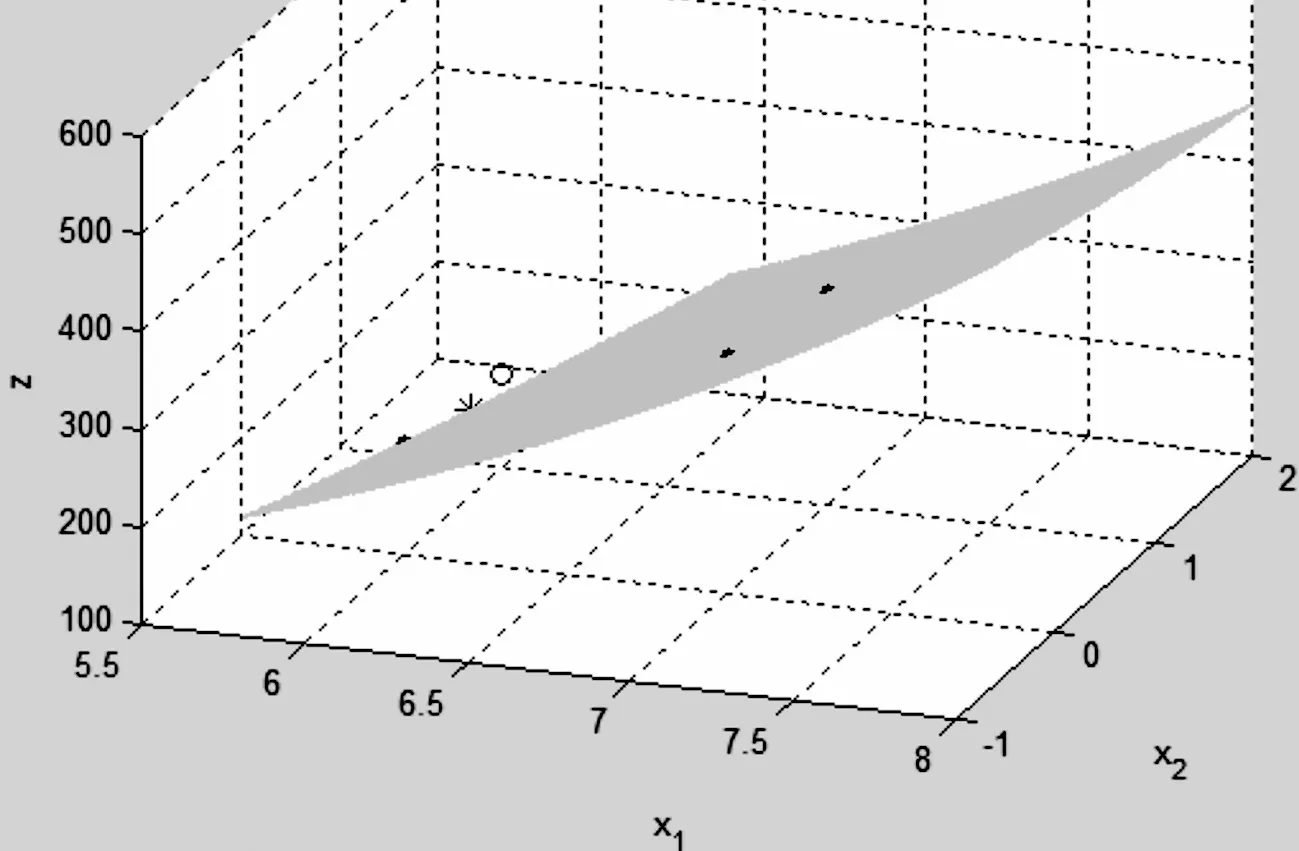
图4 整数最优解落在连续最优解的四周:视角为(20,30)
图4是从视角(20,30)方向看这5个点的结果.可以清晰地看到点(6,1,195)落在可行区域外,其z值比其他点都小,但不是最优值.
综上可得,在课堂上,利用数学软件把寻找最优解的过程动态形象的展现出来,配以较为抽象的数学理论解说,大部分学生容易当场接受.实践表明,课堂气氛活跃,学生兴趣大大提高.
5 结论
此次数学模型课程改革中,把科学计算可视化引入到教学中来,并进行了大胆而深入的课堂实践,取得较理想的效果,其可行性在于本课程的案例往往都是较复杂的实际问题,数据处理、求解过程和结果的图形展示都是极为必要的环节,而相关软件能较为方便地提供这些展示功能.在改革实践中,教师并没有遇到难以解决的技术问题,授课情况良好,而学生更形象深入地接受了知识并运用到实践中去.学生团队研讨式学习是一个新的尝试,可以清楚看到,学生能动起来,确实也动了起来.学生的自主学习意识和团队协作学习能力都得到实践锻炼.
参考文献:
[1]百度百科.可视化[EB/OL].http://baike.baidu.com/view/69230.htm,2012,11.
[2]邓飞,周亚同.基于曲面插值的剖面三维块状地质建模[J].微电子学与计算机,2009,26(9):173-176.
[3]赵改善.科学可视化研究现状[J].石油物探译丛,1996(1):1-9.
[4]唐伏良,张向明.科学计算可视化的研究现状和发展趋势[J].计算机应用,1997(3):8-10.
[5]郑秀琴,杨晓春.Matlab在数学教学中的可视化研究[J].高师理科学刊,2006,26(3):102-104.
[6]高翠云,汪莉丽.利用Matlab进行电磁学计算及可视化教学[J].电气电子教学学报,2006,2:92-94.
[7]任宪臻,莫修明.Matlab数据可视化在高等数学教学中的应用[J].数字技术与应用,2012(2):172-173.
[8]邹江涛,许传炬.可视化的科学计算[J].厦门科技,1999(1):10-11.
[9]张仁津,邓静.可视化计算机教学的研究[J].贵州师范大学学报(自然科学版),2004,22(1):118-122.
[10]师钦贤,郝金粮,夏峰俊.基于Matlab的高等数学可视化的应用研究[J].科技创新导报,2012(3):2-3.
[11]姜启源,谢金星,叶俊.《数学模型(第四版)》[M].北京:高等教育出版社,2011.
[12]Peter M.Senge.The Fifth Discipline:The Art and Practice of the Learning Organization[M].New York: Doubleday Currency,1990.
[13]陈国权.团队学习和学习型团队:概念、能力模型、测量及对团队绩效的影响[J].管理学报,2007(5):602-609.
[14]胡越,宋青青.大学生团队学习模式[J].中国证券期货,2012,7:251-253.
[15]陈一星.团队在学生学习中的作用探析[J].江苏教育研究,2006,11:12-14.

