城市污染扩散规律数学模型研究
胡恺峥 袁海明 陈达宝 伊晓颖 周燕微
(绍兴文理学院 数学系,浙江 绍兴3312000)
随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出.如何找到城市大气和土壤环境污染的污染源并予以治理,成为人们日益关注的焦点.
对于城市污染问题的研究,一般是通过对城市中污染元素含量的测定,并根据一定的标准来判断此城市的污染状况.本文的研究方法是:在一定范围内的具体位置进行数据测量,测定其污染元素及其含量,通过这些观测点的污染元素含量来研究整个城市的污染状况.本文以大气和土壤污染为例,利用质量守恒定律来建立模型,解出污染物的浓度函数,从而确定污染源,以加快污染问题的治理进程.
1 大气污染扩散模型
大气中的污染气体主要来源于工业废气、汽车尾气的排放,而这些污染气体主要是通过扩散进行传播.所以,我们将根据流体动力学中的质量守恒定律来研究大气扩散模型[1-2].
1.1 大气污染扩散模型的建立
我们以污染源为原点建立坐标系,定义距离污染源l处的污染元素浓度为ρ(x,y,z,l),因此,污染源处污染元素浓度为ρ(x,y,z,0).

图1 空间域示意图

空间域Ω内污染元素的增量为
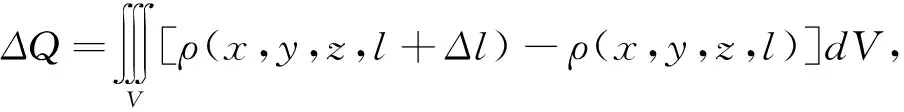
从污染源释放污染元素的总量为

其中p0为各个污染物浓度的平均值.
根据质量守恒定律和气体泄漏的连续性原理[3],即单位距离内通过所选球面S1向外扩散污染元素的质量与球面S1内污染元素增量之和,等于污染源在单位距离内向外释放污染元素的质量,即Q0=Q+ΔQ,所以

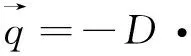
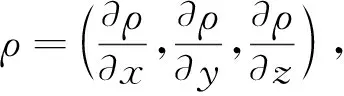
又根据曲面积分的Gauss公式

所以

即

由此可得

这样我们就得到了气体扩散的模型为
1.2 模型的求解及污染源的确定方法
求解上述气体扩散模型可得[5],任意污染处P(x,y,z,l)的污染元素浓度为
(1)
其中k为常数.
通过样本数据处理,污染物浓度的平均值为p0=176.4125ug/g.由于k和D只影响模型的峰度,不影响模型中心位置的坐标.经实验说明k的取值范围在[0.05,0.25]之间比较符合客观事实,其中扩散系数D的取值范围为[0,1].因此,在(1)式中,不妨令系数k=0.1,扩散系数D=0.1,距离l=1 000 000m.

图2 气体扩散机制图
下面求污染源的坐标.先对大量测量数据进行筛选,将浓度偏差较大的异常点删除,再把处理后的污染元素浓度值ρ(x,y,z,l)代入公式(1),利用程序可得到该浓度下的一组解.如图2所示,根据气体扩散机制[5],即污染源以球面的形式向外扩散,距污染源越远污染元素的浓度越低,且离污染源相同距离处污染物元素的浓度相同,便可寻找到该组坐标下的圆心,由此可得该浓度下的污染源坐标.把测得的浓度代入(1)式,将计算得到的该浓度下的坐标和现实中污染元素的坐标进行比较,再对求得的污染源坐标进行坐标变换,可得现实坐标系下的污染源坐标.在上述的各系数的取值下,通过程序计算得到,其污染源位置为x=5515.6,y=10722.
我们将理论结果与实际情况进行对比,发现此气体传播模型能较好地确定污染源的位置,所以本模型能较好模拟出气体扩散的规律,并找出污染源.这也为各种气体泄漏、瓦斯爆炸等突发事件有效快速的解决提供了可能,从而节约了一定的社会成本.此外,也为治理城市污染提供了有效途径.
2 土壤重金属传播模型
2.1 土壤重金属传播模型的建立
地表径流冲刷是表层土壤中重金属的主要传播途径[6],因而对流是最主要的传播特征,而扩散所起的作用相对来说较小.
记ρ=ρ(x,y,t)为t时刻位于点M(x,y)处重金属元素的浓度.利用微元法,任取一小段时间[t,t+Δt]及任意区域ω,为方便起见,记x=(x,y)T,则在微小时间段[t,t+Δt]内,污染物通过区域ω的边界∂ω进入该区域,由流体的质量守恒定律可得
其中v为污染元素的流速,即污染物在单位时间内通过的距离.
由Green公式,上式可写为

由t和ω的任意性,可得对流方程[7]
(2)
假设污染物在土壤中的流速较小,则由达西定律[8]可得

(3)
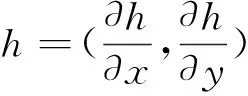
将(3)代入(2),得到

即

给定初始时刻t=t0时污染元素的浓度
ρ(x,t0)=ρ0(x),
由此得到重金属的传播模型为
(4)
2.2 模型的求解及污染源的确定方法
由于在模型的求解过程中需要用到高度函数h,因此需要先根据测得数据的高度信息确定高度函数h.又考虑到我们测量到的数据分布呈散乱状况,因而采用散乱数据插值方法得到高度函数.利用Matlab软件,运用“V4”插值法[9]得到高度地形分布图,如图3.
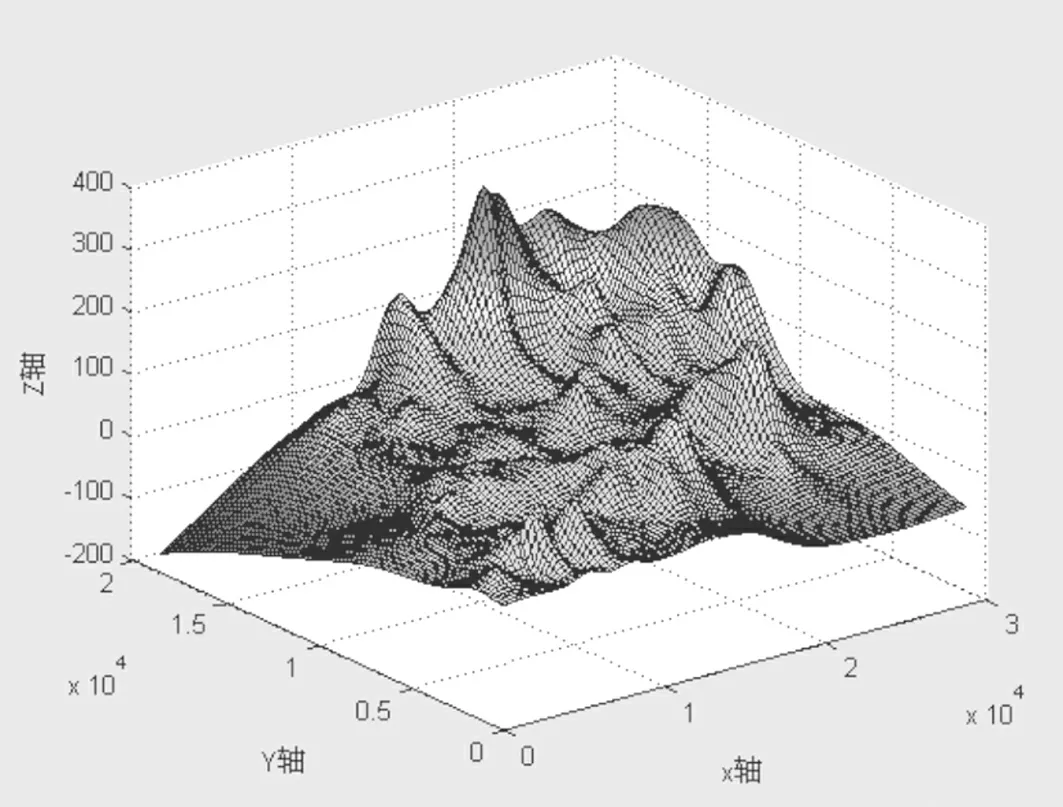
图3 “V4”插值地形分布图
由于模型(4)是一个一阶双曲型方程,可以利用特征法[10]求解.(4)的特征线满足

(5)
记过(t0,x0)的特征线为x(t,x0),重金属元素浓度ρ满足

(6)
从而沿特征线的解为

(7)
假设T时刻测量点处污染元素的浓度为ui(i=1,2,…,n),则初始条件可写为
ρ(xi,yi,T)=ρi,(i=1,2,...,n).
由于只有一个时间点上的截面数据,无法确定系数k的值,因此对时间t作伸缩变换,即令
t′=kt,
则方程(6)可改写为(为方便起见,仍记t'为t)

由特征线法可得,沿特征线(7)污染元素的浓度为

(8)
其中ρT为T时刻xT处测得的污染元素的浓度.
对(5)和(8)分别作离散化,得到迭代格式
xm+1=xm+▽h(xm)Δt,
(9)

(10)
其中ρ0为T时刻污染元素的初始浓度.
若在某一给定点x0处的浓度为ρ0,则由(9)及(10)可以求出各时刻t(t≤T)沿着经过点xo处的特征线上的浓度值ρ(x,t;x0).这样,当给定污染浓度的阈值U时,对给定时刻t1(t1≤T),浓度超过阈值U的区域为
Bi={x(t1)|ρ(x(t1),t1;x0)≥U},
此区域即为可能的污染源所在的区域.
根据特征线法我们画出了污染元素浓度图,如图4;根据测得的污染物数据,我们画出了污染元素浓度的测量值,如图5.从图中看,我们发现用特征线法求得的污染元素浓度与测量得到的浓度非常接近.同时,我们将坐标M(x,y)的值代入(7)式计算得到的浓度与测量得的浓度进行比较,发现两值也非常接近.

图4 用特征线法得到的污染元素的浓度 图5 污染元素浓度的测量值
本模型适用于各种由于对流造成污染的重金属,包括河流中的污染等,不仅可以根据测量的污染物浓度确定污染源,为治理污染省去大量的人力物力,加快治理污染的过程,而且可以根据污染源计算出距离污染源多少远处污染物的浓度,为合理建造化工厂等提供相应的对策.
3 结论
我们利用流体力学中的质量守恒定律来建立城市大气污染扩散模型和土壤污染扩散规律,得到污染物的浓度函数,由此得出污染源.这为城市气体泄漏、瓦斯爆炸、土壤重金属污染等突发事件提供了有效快速的解决途径,有利于快速找到泄漏地点,解决突发事件,且省去了大量的人力、物力,节约了大量的社会成本.
致谢
本文是在陈志祥和胡金杰老师的指导下完成的,在此表示谢意.
参考文献:
[1]姜启源,谢金星,叶俊.数学模型[M].北京:高等出版社,2003.
[2]王冬琳.数学建模及实验[M].北京:国防工业出版社,2004.
[3]刘振翼,周轶,黄平等.CO2管线泄漏扩散小尺度实验研究[J].化工学报,2012年,63卷(5):1655-1657.
[4]何龙庆,林继成,石冰.菲克定律与扩散的热力学理论[J].安庆师范学院学报,2006,12(4):38-39.
[5]石东伟,陈冬娜.高斯扩散模型在确定污染源位置中的应用[J].河南科技学院学报,2012年,40卷(2):57-58.
[6]高存昌.沼气在农业面源污染治理中的作用[J].河南农业,2012(5):6-7.
[7]Ockendon J,Howison S,Lacey A,et al.应用偏微分方程[M].北京:科学出版社,2008.
[8]蒋玄苇,张野,王嘉舜.地下水在平面渗流状态下的流速测定[J].科技资讯,2012(8):100-101.
[9]马莉.Matlab数学实验与建模[M].北京:清华大学出版社,2010.
[10]Lin Changrong1,Wang Shangxu,Zhang Yong.Predicting the distribution of reservoirs by applying themethod of seismic data structure characteristics: Examplefrom the eighth zone in Tahe Oilfield[J].Applied Geophysics,2006(4):234-240.

