预应力风电机组基础与风电机组塔架连接分析
孙羽,李昂
(新疆水利水电勘察设计研究院,乌鲁木齐 830000)
0 引言
法兰连接是目前所有筒形件连接最常见的连接形式,具有整体刚度好、可靠性高、安装方便等优点[1]。
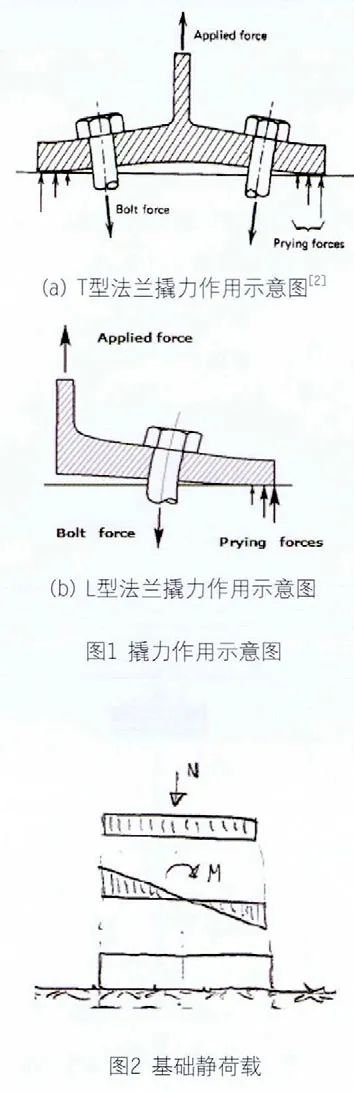
法兰按照有无加强筋可分为刚性法兰和柔性法兰。 柔性法兰在受力过程中会产生变形,但是由于连接的阻挠刚度,在接近翼缘边外会产生额外的力,这种现象叫做撬开作用(见图1)[2]。撬开作用增加紧固件的力并且对紧固件的强度和性能不利。撬开力的大小主要取决于连接件的刚度。
Douty和Mc Guire[3]采用数学模型分析了撬开作用机理,并提出了根据弹性分析的半经验公式。但是这个公式过高估计了撬开力而得到保守的设计结果,并且该经验公式只适用于他们研究的特殊的螺栓和板材的组合,不同螺栓-板材的组合需要不同的公式。Struik J. H. A.和 Back J. de[4]在Douty和Mc Guire的半经验公式基础上做了改进,获得一个撬开力近似计算公式,但是这个公式得到的结果也是相对保守的。之后,Fisher J W和Struik J. H. A.[2]又做了修正,得到了静荷载条件下的法兰连接设计撬力计算公式。然而迄今为止,所有关于撬开力的研究都是假定法兰连接在刚性底面上。
法兰按结构形式可分为L型法兰和T型法兰。其主要应用在压力管道的连接、风电机组塔筒的连接等一些多筒段结构的连接中。L型法兰在风电机组中主要用于塔筒段之间的连接,而在塔筒与地基浆料或者混凝土的连接中却并没有采用L型法兰,而是采用T型法兰。
风电机组塔筒与高灌浆料之间连接的相关分析却少之又少,而且对于 L型法兰是否适合于直接应用在与地基高灌浆料的连接中,没有相关文献或规范给出说明。若是将L型法兰用在与混凝土连接中,由于混凝土的支撑面并不是刚性的,在这种情况下撬开力的大小和位置是由法兰连接的翼缘和底面的相对刚度决定的。在这种连接中所得到的荷载情况是高度负载的,而且还没有充分研究过。因此,前人给出的设计公式已不再适用。
本文将针对风电机组塔筒与地基的连接系统中采用标准的L型柔性法兰进行分析,并根据分析结果给出L型法兰是否适用于风电机组塔基与地基高混凝土之间的连接的理论依据以及判定结果。
1 L型法兰与地基混凝土连接理论分析
1.1 荷载分析
由于基础是一个系统,应该考虑基础的不同部分。因此,在分析其受力时的荷载需考虑周全。相关基础荷载由下列各项组成:a.从锚件转移到塔架法兰的反作用;b.基础与回填土的静荷载。
当考虑嵌入件的细部时(例如混凝土与嵌入法兰件的接触压力,防止向下和向上冲压的钢筋),采用塔架反作用。塔架反作用应添加在塔底座法兰层面上。
1.1.1 基础静荷载
法兰嵌入基础层面处,来自塔架的反作用由以下部分组成:沿着塔架静荷载圆周线的线荷载和嵌入法兰层面处的弯矩。
塔架静荷载:

嵌入法兰层面处弯矩:

式中:Fz——塔架竖向力;
γG——Fz分项系数,取决于是有利荷载(迎风面)还是不利荷载(背风面);
Mres,Fres——塔架弯矩;
eF——Fres的偏心率,等于从塔底座法兰到基础底面的距离。
1.1.2 隔离体荷载
锚件沿塔架壳体直径圆周均匀分布,锚件上荷载的计算通过提取出一个锚件的小段以及带有塔架壳体与法兰塔架段的隔离体来进行分析。
已知每段塔架壳体内的极限荷载(每小段):

式中:Na,D——分别为隔离体数目和分布直径。
由于弯矩作用,塔架法兰在迎风侧受拉而在背风面受压,所以每个小段上的总荷载为(此处为向上为正):
迎风侧:


背风侧:锚件为后张。在已知锚件与混凝土的弹簧刚度时,可计算由锚件承受的部分外荷载。在Stahlbau第23.2.10.4章中给出了一种普遍的计算方法[5],但是对于T型法兰和L型法兰要分别进行对待。因为T型法兰由于自平衡性不必考虑法兰弯矩的作用,而L型法兰受弯矩的影响要考虑更多的因素。
1.2 L型法兰隔离体荷载分析
L型法兰与T型法兰的不同之处在于:L型法兰采取的是锚栓一侧固定,这样在受到外荷载时就会引起弯矩的作用,弯矩又会压迫下方灌浆和混凝土向一边倾斜。所以对于L型法兰不仅要计算不考虑弯矩时混凝土的弹簧刚度,还要考虑混凝土截面的抗弯抵抗矩。
1.2.1 不考虑弯矩对L型法兰连接的影响
此时,即将隔离体的外荷载移至锚杆的中心,使作用力都在一条直线上,此时受力简化图如图3所示。
在不考虑弯矩的情况下,L型法兰与混凝土连接结构中锚件的受力情况与T型法兰是相似的,由于锚件是后张锚,所以在施加外荷载Ptd后,锚件的预张拉力会有一定损失,假设损失系数为p,则可得到如下等式:


横截面为Aa且长度为La的钢锚杆将具有弹性弹簧刚度:


L型法兰压制混凝土的体积也被假定为梯形并以中间锚杆为轴对称,这样,L型法兰下混凝土的弹簧刚度就与T型法兰下混凝土的弹簧刚度计算方法一样,通过推导可以得出:

p的典型值为8%~10%,由于压制混凝土部分的减载,该典型值表明了大约10%的外荷载影响着锚件的预张拉力。
在不开裂的情况下,即法兰与灌浆刚好完全接触,此时锚件内的受力为:

1.2.2 弯矩对L型法兰连接的影响
在弯矩的作用下,迫使法兰产生转动,一边脱开与灌浆的接触,另一边紧紧压入混凝土中。由于钢筋跟混凝土的弹性模量相差较大,因此可以将法兰近似看作刚体,这样就可以将问题大大简化。
在刚好不脱开的情况下,弯矩作用使法兰产生绕锚点的转动弧度刚好等于在不考虑弯矩时混凝土的被压缩量,如图4所示。由此可求出弯矩对L型法兰连接结构受力的影响。

式中:R——为法兰对混凝土的压力;
M——为与Pa不在一条直线上的Ptd引起的绕锚点的弯矩,
W——为法兰下受压混凝土的有效截面地抗矩。
由图3可知,法兰下面受压混凝土截面为两个等腰梯形,为了计算它的截面抵抗矩,通过将其等效为一矩形柱体,如图5所示。
则此等效受压混凝土的有效截面抵抗矩为:

将式(13)代入式(12)中,便可以推导出在弯矩作用下混凝土对法兰的作用力:
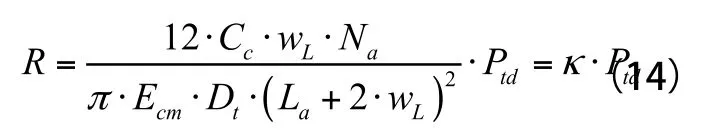


1.2.3 L型法兰连接中锚件的预张拉力
综合考虑1.2.1和1.2.2节的内容,可以获得此时锚件受到的拉力为:


1.2.4 法兰下方的应力
(1)受拉侧法兰下方应力
计算塔架L型法兰下的灌浆应力和其正下方的混凝土内的应力时,需要单独考虑弯矩作用产生的应力,其简易方法将使用以下公式:

灌浆:

混凝土:

(2)受压侧法兰下方应力
L型法兰受压侧下方的灌浆及其混凝土的应力计算时与受拉侧不同,由于外荷载的方向与锚杆力的方向相同,因此要考虑外荷载对锚杆应力的损失的影响。

式中

2 L型法兰有限元分析验证
2.1 坐标系及极限荷载
为了进一步验证理论分析结果,现采用金风科技70/1500风电机组进行有限元模拟。基础荷载的计算数据采用极限荷载工况下塔基法兰处的荷载数据(不含放大倍数),见表1。
坐标系采用GL规范坐标系,如图6所示。

表1 极限荷载工况下塔基法兰处荷载
2.2 法兰及基础尺寸数据
基础为半径为2.5m,高度为2.85m的混凝土圆柱体。上下法兰之间锚杆的长度为2.597m。其各部分之间的尺寸数据详见图7。
2.3 理论计算结果
根据以上输入数据,可以求得理论分析结果,现汇总于表2中。
从表2中可以清楚看出,L型法兰与混凝土连接结构需要很大的锚杆初始张拉力,此时锚杆在极限荷载作用下并未达到屈服。在极限荷载工况下,由于弯矩的作用迫使L型法兰下方受压侧灌浆受到的应力也相当大,在受压侧最大应力达到95.54MPa,超过了灌浆的屈服强度,故灌浆料将会被破坏,风电机组会倾斜,产生安全隐患。
2.4 有限元分析结果

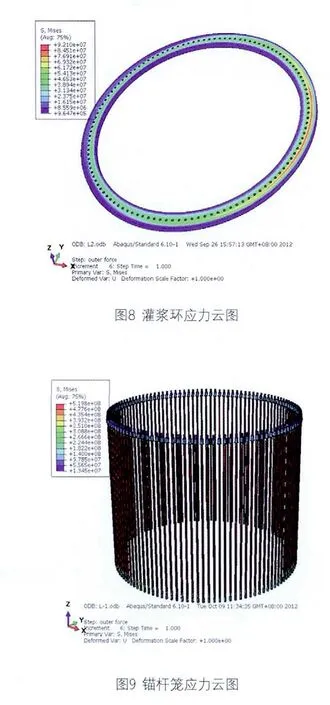

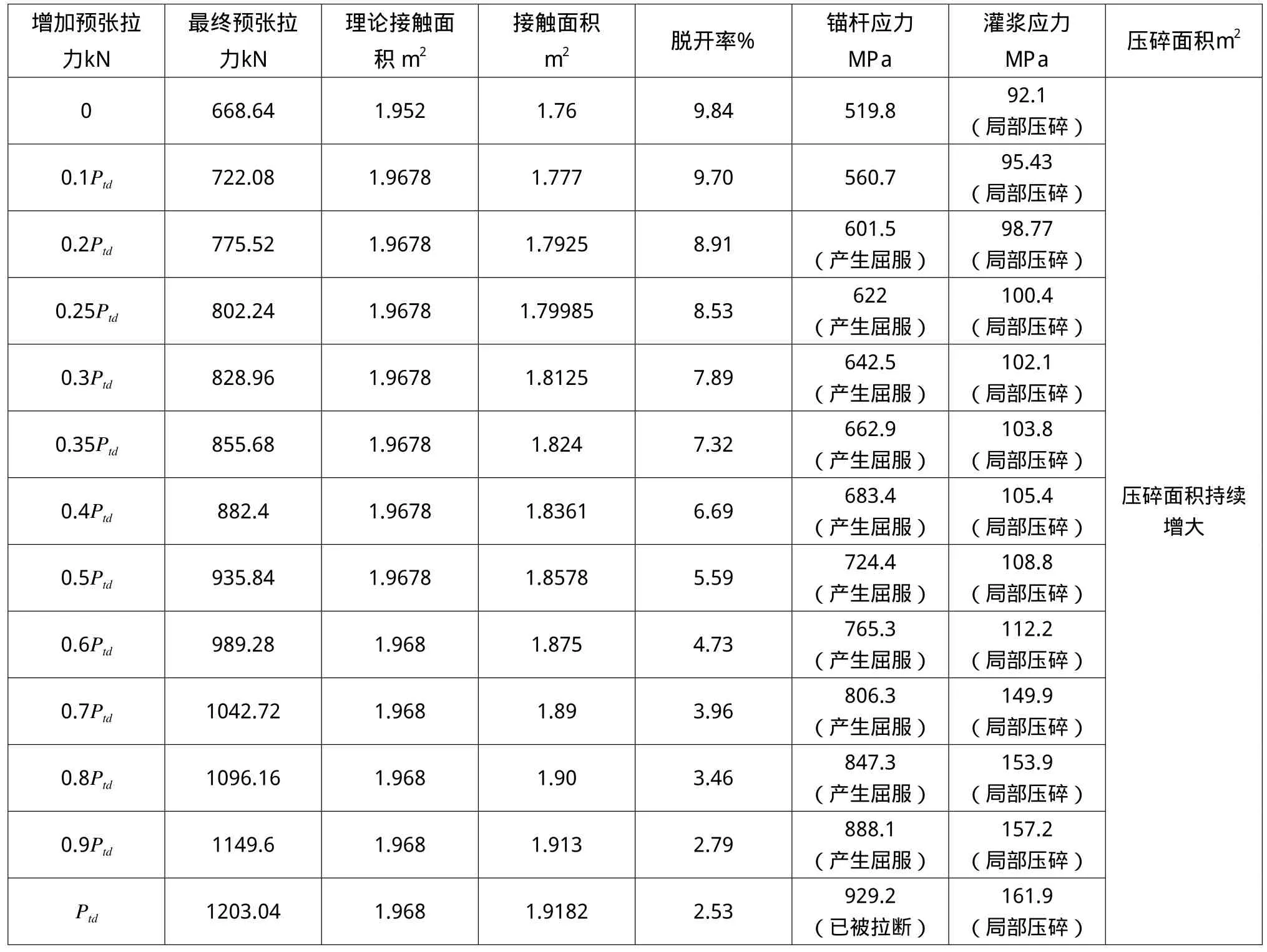
表3 各预张拉力下有限元结果]
通过ABAQUS有限元软件对极限荷载工况下L型法兰与地基连接系统进行模拟仿真,有限元分析结果见图8和图9。并提取出法兰与灌浆接触面在荷载作用下的接触面积以及沿灌浆接触面上最大最小应力路径上的应力曲线,如图10所示。
从图8、图9以及图10(b)中可以看出,有限元模拟结果与理论分析结果十分接近,证明了理论公式的正确性。但是从图10(a)中同时可以看出,法兰与灌浆料圆环之间的接触并非完全紧紧闭合在一起。法兰若是与灌浆完全接触的面积应为L型法兰的底面积:
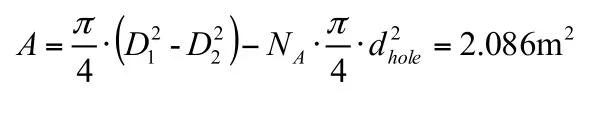
但是在极限荷载工况下,由有限元分析结果可以看出,在施加螺栓预张拉力后,L型法兰与高灌浆料的接触面积减小为1.952m2,说明在施加预张拉力后,法兰发生翘曲使接触面积开始就减小,在极限荷载作用下,法兰与灌浆的接触面积减小至1.76m2,接触面积又减小了9.84%。究其原因,法兰的刚度虽然比灌浆的刚度要大很多,但仍不是刚性法兰,在极限荷载作用下自身仍会产生翘曲变形,即撬力作用,但这种情况下的撬力计算相当复杂。
由于L型法兰与灌浆之间并没有完全接触,而且目前世界上对于法兰连接之间的脱开面积占总面积的百分之几时连接仍然有效没有给出过说明,所以在现有预张拉力基础上继续增大,直到法兰与灌浆料之间的完全接触,各预张拉力下结果汇于表3。
从表3中可以看出随着锚杆中施加预张拉力的增大,脱开面积逐渐减小(不考虑灌浆被压碎面积,实际灌浆料已经开始被压碎),但是随着预张拉力的增大,锚杆内的应力也随之增加,锚杆开始产生屈服,当预张拉力增加到一定值的时候锚杆已经被拉断,此时法兰与灌浆之间的脱开率已经降到了2.53%,仍然没有完全接触,而且随着初始预张拉力的增大,灌浆中被压碎的面积的逐渐增大。因此,基础在采用L型法兰情况下无论怎样都不能满足要求。
3 结论
从计算分析结果来看,现有研究可以得到以下结论:
(1)现有L法兰虽然与灌浆及混凝土相比,具有相对较大的弹性模量及抵抗变形的能力,但仍不能将其视为刚性体来处理。在实际情况下,法兰在大预张拉力及外荷载作用下仍会产生变形。
(2)随着锚杆上施加的初始预张拉力的增大,法兰与灌浆之间的接触面的脱开率也逐渐减小(假设灌浆不被压碎)。当施加初始预张拉力达到775kN,在极限荷载工况下,锚杆开始屈服,当初始预张拉力达到1200kN,此时锚杆已经被拉断,而此时仍有2.53%的脱开率。
(3)随着锚杆上施加初始预张拉力的增大,同样灌浆上受到的应力也随之加大,被压碎灌浆的面积也同样增大,因此随着预张拉力增大也不能达到理想的效果。
因此,在风电机组的塔基与基础之间的连接中,不适合直接采用L型法兰同混凝土或者高强灌浆料直接连接。同时根据笔者同中国建筑科学研究院相关专业人员的沟通,直接采用更高强的灌浆料也不可行。因为高强必然带来脆性变大,脆性过大已经不能满足在基础灌浆中使用要求。
对于法兰直接与混凝土或者浆料相连的解决方案,目前国外方案为直接更换T法兰或者加装一个T法兰转接头。这样就能够避免各种设计中的问题。
[1] 王元清,孙鹏,石永久. 圆钢管法兰连接承载性能的有限元分析[J]. 钢结构, 2009, 8(24): 16-20.
[2] 王志遂, 译. Fisher J W, Struik J H A. 螺栓和铆钉连接设计准则指南[M].北京: 人民交通出版社, 1983.
[3] R. T. Douty, W. McGuire. High Strength Bolted Moment Connections[J].Journal of the Structural Division, ASCE, 1965, 91.
[4] J. H. A. Struik, J. de Back. Tests on Bolted T-Stubs with Respect to a Bolted Beam-to-Column Connections[R]. Stevin Laboratory, Delft University of Technology, Delft, the Netherlands, 1969.
[5] Petersen, Chr.: Stahlbau. Friedr. Vieweg & Sohn[M]. Braunschweig /Wiesbaden, 1988.

