淤地坝控制黄土高原坡沟系统重力侵蚀的空间特征

邹兵华，袁 洁，李占斌，李 鹏

（1.中国水电顾问集团成都勘测设计研究院，四川 成都610072；2.西安理工大学 西北水资源与环境生态教育部重点实验室，陕西 西安710048；3.西安理工大学 水利水电学院，陕西 西安710048）

黄土高原沟壑纵横，支离破碎，有大小沟壑27万多条，沟壑面积占土地总面积的20%～40%，是世界上水土流失最严重的地区之一，其支离破碎的地貌主要由沟蚀造成［1－2］。黄土高原的各类沟壑中以沟头前进、沟底下切、沟岸扩张三种形式的沟蚀危害最为严重［1－2］。沟蚀造成了更多的陡峭临空面，加剧了重力侵蚀［2－4］。重力侵蚀是指地表物质在重力作用下，分散或成块，急速或缓慢向下移动的过程，主要表现形式有土的蠕动、松散物的滑动、松散物的流动和崩塌等［5］。重力侵蚀直接或间接地向河道输送了大量的泥沙，是流域土壤侵蚀和河流泥沙来源的主要物理过程之一，并在区域地貌演化中扮演了十分活跃的角色［6－9］。根据黄河水利委员会的西峰、天水、绥德3个水保站在典型小流域的调查，这些地区的重力侵蚀面积和侵蚀量均占很大比例，重力侵蚀十分严重［2，8－9］。1986年以后，由于沟道打坝抬高了侵蚀基准面，稳定了沟壁，加之沟谷大多种植了林草，据实地观测没有上述情况出现，沟壁的扩张得到制止［10］。在黄土塬区和丘陵区，沟头前进多以土体崩塌形式进行，沟岸扩张是崩塌与滑 坡 共 同 作 用 的 结 果［2，8－9，11］。 淤 地 坝控制重力侵蚀的作用是在沟道建坝以后开始的，其减蚀量一般与沟壑密度、沟道比降以及沟谷侵蚀模数等因素有关［12］。沟道里修建淤地坝以后，随着坝前泥沙的淤积，抬高了侵蚀基准面，可防止沟道下切和沟岸坍塌，减少沟道侵蚀；坝内淤积厚度的不同，对重力侵蚀的控制程度不同，且坝内泥沙的淤积厚度越大，对重力侵蚀发生的控制越为有利［13］。

坡沟系统是黄土高原小流域特有的结构。黄土高原的坡沟系统是从峁坡坡顶经坡面、沟坡至沟道但不包括沟道的一个统一体，既是区域侵蚀产沙的主要源地，又是控制水土流失，减少下游河道淤积，恢复与重建生态环境的基本治理单元，历来为黄土高原小流域治理中理论性与实践性均很强的重要科学命题［14］。由于坡沟系统重力侵蚀的发生具有点多面广和随机性的特点，且基础观测资料相对薄弱，有关研究就更少［2，13］。

淤地坝（系）作为黄土高原地区沟道水土保持的重要工程措施，在减蚀、减沙、防洪、保收、发展地方经济等方面起到了重要作用［15－17］，而且有机结合了水土保持和致富的关系，深受黄土高原地区群众的喜爱，同时又为水利水土保持部门所关注。修坝拦泥淤地、蓄水拦沙是流域水土保持综合治理的一项重要措施，目前国内外有关淤地坝的研究主要集中在坝系相对稳定性，减蚀减沙，滞洪保收和生态环境效应等方面，而对淤地坝控制坡沟系统重力滑坡侵蚀方面的研究则少有人提及。坝地淤高后抬高了沟底的侵蚀基准面，增强了沟坡的稳定性，减少了沟坡重力侵蚀发生的可能性。那么坡沟系统的稳定性和重力滑坡侵蚀中峁坡和沟坡对沟道侵蚀产沙的贡献随着坝地的逐渐增高到底是如何变化的呢？本研究通过数值模拟，对随着坝地的逐渐淤高而产生的坡沟系统的稳定性、滑塌量以及坡沟系统重力滑坡侵蚀中峁坡和沟坡所占比例等方面进行研究，以期为小流域沟道重力滑坡侵蚀的预报和分析评价提供重要参数和科学依据，并为评价坡沟系统的稳定性提供一定可靠度的依据。

1 研究区概况

本研究选取王茂沟流域左岸的典型支沟——关地沟作为研究对象。王茂沟是陕北绥德县韭园沟中游左岸的一条试验性治理支沟，为无定河的一条2级支沟，海拔高度940～1 188m，流域面积5.97km2，主沟长3.75km，沟道平均比降为2.7%，沟谷地面积2.97km2，占流域总面积的46.7%，沟壑密度4.3km／km2［2，17］。地形地貌主要由梁、峁以及分割梁峁的沟谷组成，沟内地形破碎，沟壑纵横，坡陡沟深。梁顶和峁顶面积不大，均略成穹形，坡度在8°～10°，梁、峁坡的坡度，一般在20°～35°；梁、峁坡以下为沟谷，沟谷横断面在上游及支沟均呈“V”字型，在下游略呈“U”字型。沟谷坡极陡，一般在35°以上。按土壤侵蚀区划，属黄土高原丘陵沟壑区第Ⅰ副区［2，17］。

流域属北温带干旱大陆性气候，年平均气温10.2℃，夏季多东南风，春秋多西北风。流域多年平均降水量513.1mm，降雨量年际变化大，年最大降雨量是年最小降水量的3.5倍；降雨年内分配极不均匀，年内降雨量主要集中在汛期7—9这3个月，汛期降水量占年降水量的73.1%，且多以暴雨形式出现，一次暴雨产沙量往往为全年产沙量的60%以上，土壤侵蚀以水力侵蚀及重力侵蚀为主，治理前属剧烈侵蚀区，在黄土丘陵沟壑区具有一定的代表性［2］。

2 研究方法

2.1 重力滑坡侵蚀分析的极限平衡法

目前应用于边坡稳定分析的方法主要有基于极限平衡的传统方法和有限元法［18］。极限平衡法（如瑞典圆弧法、Bishop法、Janbu法）是边坡稳定分析中最常用的方法，它通过分析坡体在临近破坏的状况下，土体外力与内部强度所提供抗力之间的平衡，计算土体在自身和外荷作用下的土坡稳定性的程度。传统的边坡稳定性分析方法中，为了便于分析计算做了许多假设［19－22］，如假设一个滑动面、不考虑土体内部的应力—应变关系等。因此，传统分析方法不能得到滑体内的应力、变形分布状况，也不能求得岩土体本身的变形对边坡变形及稳定性的影响。在边坡稳定分析中引入有限元法始于20世纪70年代［20］，有限元法克服了传统分析法的不足，不仅满足力的平衡条件，而且还考虑了土体应力—变形关系，能够得到边坡在荷载作用下的应力、变形分布，模拟出边坡的实际滑移面［19］。正因为有限元法的上述优点，近年来已广泛应用于边坡稳定性分析。

2.2 重力滑坡侵蚀的有限元强度折减法原理

有限元强度系数折减法的基本原理［19－20］是将坡体强度参数黏聚力c和内摩擦角φ，同时除以一个折减系数ω，得到一组新的c′和φ′：

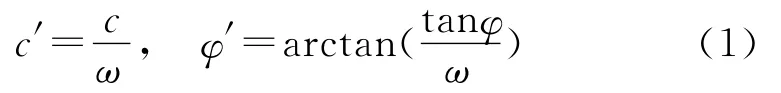
式中：c——岩土体原本的黏聚力；φ——岩土体原本的内摩擦角（°）；ω——岩土体强度折减系数；c′——岩土体折减后的黏聚力；φ′——岩土体折减后的内摩擦角（°）。

然后作为新的参数输入，再进行试算，利用相应的稳定判断准则，程序自动根据弹塑性计算结果得到破坏滑动面，确定相应的ω值为坡体的最小稳定安全系数。有关研究表明［18－22］，有限元强度折减法的安全系数在本质上与传统方法是一致的。赵尚毅等［19－20］通过多种比较计算说明有限元折系数法用于分析土坡稳定问题是可行的，但必须合理地选用屈服条件以及严格地控制有限元法的计算精度。

本研究采用节点不平衡力的不收敛作为判据，同时根据塑性区的范围及其连通状态确定相应的安全系数，屈服准则采用不等角六边形外接圆（DP1）屈服准则计算安全系数然后按式（2）转换为莫尔—库仑等面积圆准则下的安全系数［2］：

式中：η——外接圆（DP1）屈服准则下安全系数转换为莫尔—库仑等面积圆屈服准则下安全系数的转换系数；φ——岩土体的内摩擦角。

3 结果与分析

3.1 关地沟小流域沟坡系统概化模型及有限元模型

根据地质资料［17］，关地沟地层构造主要是马兰黄土（Qeol3），梁、峁顶、峁坡均有分布，厚度20～30m，其下层为离石黄土（Qeol2），厚度50～100m，多出露于沟坡上，再下层主要是三叠纪砂页岩层，基本接近水平，多出露于干沟、支沟的下游及其两侧［17］。关地沟坡沟系统概化模型土层从上到下分别为马兰黄土（Qeol3）和离石黄土（Qeol2），厚度分别取为土层厚度的平均值25和75m。通过实测数据的统计分析，峁坡坡度在21°～25°所占比例最大，达到50%，而实测坡度在21°～25°范围内的平均值为23.1°，取峁坡坡度为24°；沟坡坡度在36°～45°所占比例最大，达到43.6%，而实测坡度在36°～45°范围内的平均值为40.8°，取沟坡坡度为41°［2］。

坡沟系统的计算采用平面应变条件下摩尔—库仑不等角六边形外接圆屈服准则（DP1）和非关联流动的理想弹塑性模型［23－25］。坡沟系统基岩底边界为固定约束，左边界为水平约束。弹塑性有限元计算采用大变形静态分析选项，最大迭代次数为1 000［2］。

3.2 计算参数取值

根据边坡工程经验、现场查勘及室内岩土物理力学试验［17，26－29］和有限元计算的需要，坡沟概化模型各土层材料特征取值如表1所示。

表1 关地沟坡沟系统的计算参数

3.3 关地沟小流域随坝地淤高沟坡系统稳定性的变化

关地沟4号坝从1959年修建到1987年被洪水冲毁的28a运行过程中，累计於高4.86m，年均淤高0.18m。垮坝后当地群众对坝体进行了零星修复填筑及2005年坝体修复加高，坝地的自然淤积过程遭到破坏，坝地已不再是原来垮坝前的自然淤高，截至2007年坝地累计高10.8m。由于关地沟4号淤地坝垮坝前坝地的年均於高仅为0.18m，在垮坝前的淤高模拟计算中以5a为一个时间跨度，计算坝地每淤高0.9m时的坡沟系统稳定特征参数；垮坝后为了与垮坝前保持一致性，坝地以0.9m递增。在有限元程序中，模拟坝地按0～0.9，0.9～1.8，1.8～2.7，2.7～3.6，3.6～4.5，4.5～4.86，4.86～5.4，5.4～6.3，6.3～6.48，6.48～7.2，7.2～8.1，8.1～9.0，9.0～9.9，9.9～10.8m 的 淤 积 过 程［2］，每 淤积 （增 高）0.9m其相应的稳定系数和滑塌量的散点图见图1—2。

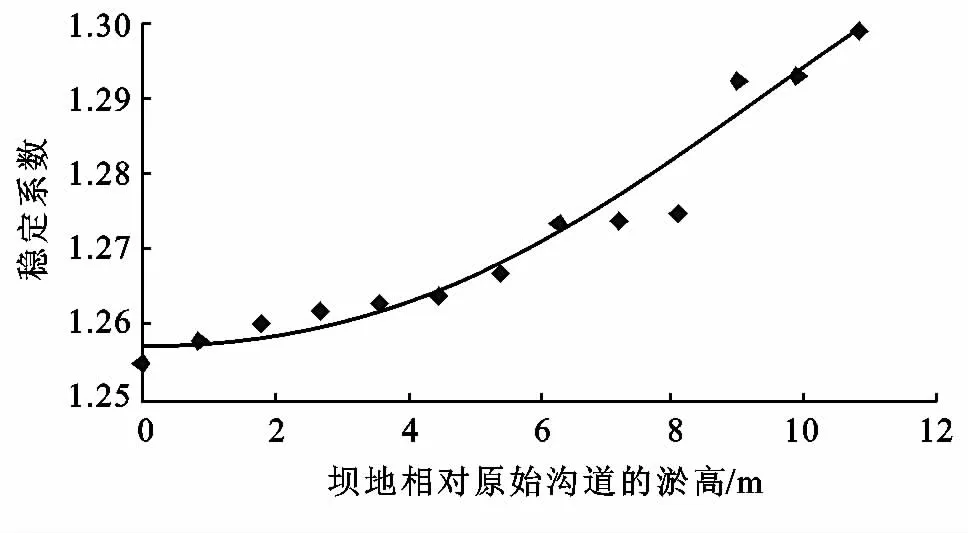
图1 随坝地淤高坡沟系统稳定系数的变化规律

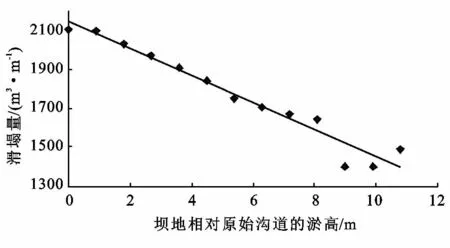
图2 随坝地淤高坡沟系统滑塌量的变化规律

由图1—2分别拟合出相关系数最高的随坝地淤高坡沟系统的稳定系数和滑塌量变化规律的相关方程［2］（如表2所示）。

表2 随坝地淤高坡沟系统的稳定系数和滑塌量变化规律

由表2可以得出，随坝地淤高坡沟系统的稳定系数和滑塌量分别满足二项式和直线分布规律，且相关性较高，可用于该沟道重力侵蚀的分析评价［2］。

由表3可得，在原始沟道建坝初期坝地还没有淤积的时候，坡沟系统稳定系数最小，由有限元强度折减法得此时坡沟系统在摩尔—库仑不等角六边形外接圆屈服准则（DP1）下的安全系数为1.507，将其按式（2）转换为莫尔—库仑等面积圆屈服准则下的安全系数为1.224，其与滑坡分析采用Spencer法求得此时的安全系数1.254 7的相对误差为2.42%，在郑颖等［19－20］的研究指出莫尔—库仑等面积圆屈服准则的安全系数与Spencer法的平均误差5%范围内，精度满足要求。限于篇幅，考虑到系统误差的一致性，其余各坝地淤高的安全系数没有两两比较，但精度满足要求。

3.4 发生重力滑坡侵蚀时峁坡和沟坡各自的滑塌量及比例

在淤地坝减蚀减沙和坡面水土保持措施效益分析计算中，一直存在一个难点就是如何如把坡面侵蚀和沟坡侵蚀的量分别计算出来。由于重力滑坡侵蚀的总体积V和总重量M是已知的（已通过软件模拟计算出来，见表3），通过式（3）及推导式（4）—（5）可分别计算得到峁坡和沟坡在重力滑坡侵蚀中各自滑塌土体的体积和重量及相应的比例（表4）。其中，Vm和Vg为峁坡和沟坡重力滑坡侵蚀土体的体积；γm和γg为峁坡和沟坡重力滑坡侵蚀土体的容重。

通过变量代换和代入消元法可得到：

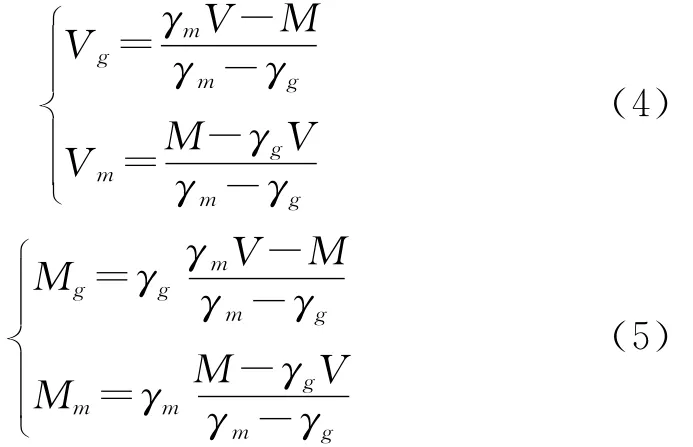
表3 随坝地淤高坡沟系统稳定系数和滑塌量计算结果

由表3—4可以看出，在坡沟系统重力滑坡侵蚀中，随着淤地坝的淤高，峁坡和沟坡滑塌物的体积和重量之比基本为1∶50；峁坡滑塌物的体积和重量占总滑塌物体积和重量的2%，而沟坡滑塌物的体积和重量占总滑塌物体积和重量的98%。在重力侵蚀产沙中，沟坡侵蚀是沟道泥沙的主要来源。

4 结论

基于边坡分析软件和有限元技术，通过建立关地沟4号坝上游典型坡沟系统的概化模型，得出随淤地坝坝地淤高，坡沟系统稳定系数的增加满足二项式分布规律，而滑塌量则满足线性减少的分布规律，两者精度均较高，可用于该沟道重力侵蚀的预报、侵蚀量的分析评价［2］。

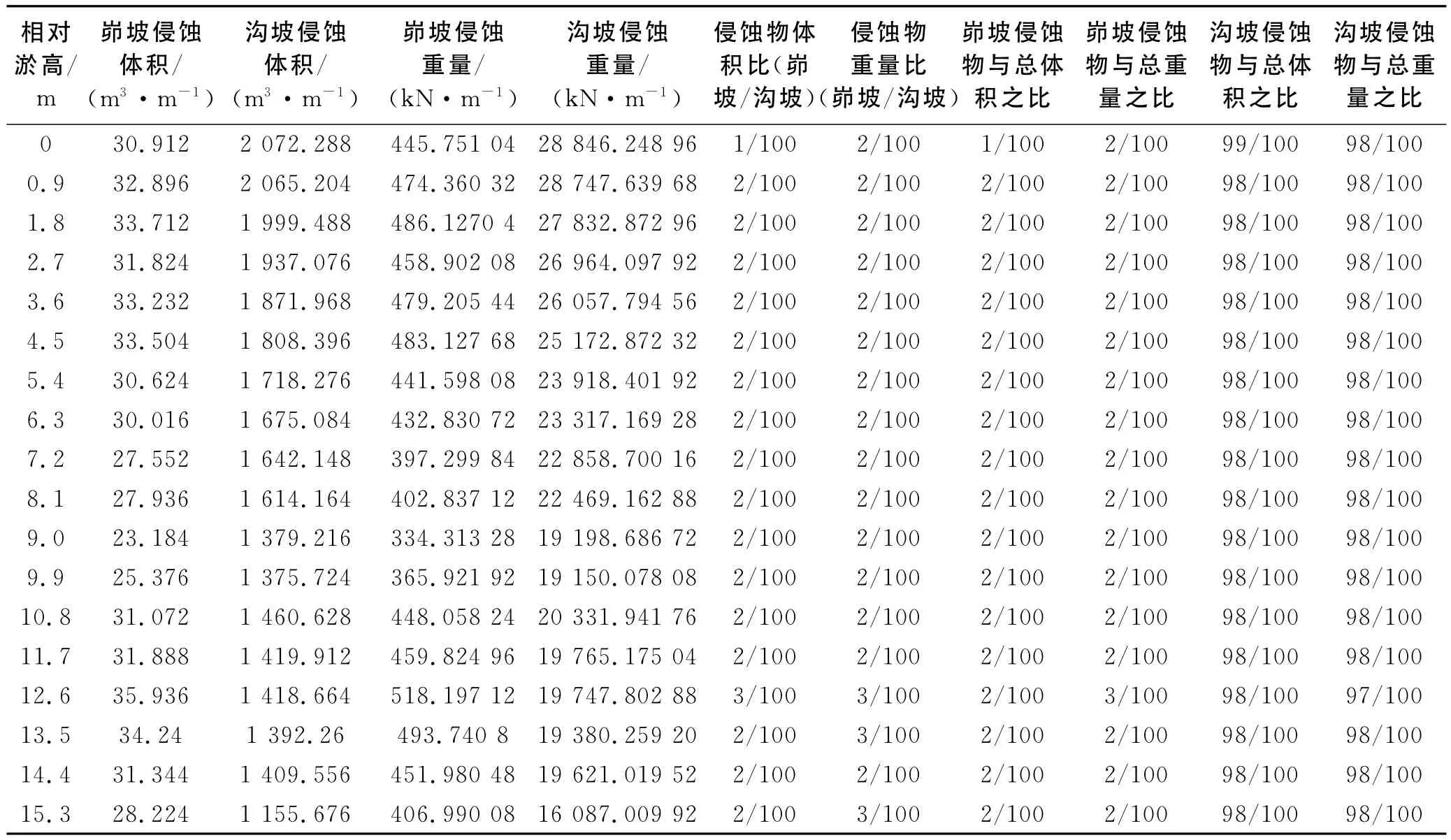
表4 坡沟系统滑坡侵蚀中峁坡和沟坡侵蚀量及所占比例

通过公式推导和软件计算分析，分别得到了峁坡和沟坡的滑塌量及各自在滑坡侵蚀总量中所占的比重。在坡沟系统重力侵蚀中，随着淤地坝的淤高，峁坡和沟坡滑塌物的体积和重量之比基本为1∶50；峁坡滑塌物的体积和重量占总滑塌物的体积和重量的2%，而沟坡滑塌物的体积和重量占总滑塌物的体积和重量的98%。在重力侵蚀产沙中，沟坡重力侵蚀是沟道泥沙的主要来源。

［1］ 唐克丽.中国水土保持［M］.北京：科学出版社，2004.

［2］ 邹兵华，袁洁，李占斌，等.淤地坝减轻坡沟系统滑坡侵蚀的数值模拟［J］.水土保持通报，2013，33（1）：265－270.

［3］ Williams J R，Berndt H D.Sediment yield prediction based on watershed hydrology［J］.Transaction of the ASAE，1977，20（6）：1100－1104.

［4］ Nachtergaele J，Poesen J，Vandekerck hove L，et al.Testing the ephemeral gully erosion model（CEGEM）for two Mediterranean environment［J］.Earth Surface Process and Landforms，2001，26（1）：17－30.

［5］ 韩鹏，倪晋仁，王兴奎.黄土坡面细沟发育过程中的重力侵蚀实验研究［J］.水利学报，2003（1）：51－55.

［6］ 焦菊英，王万忠，李靖，等.黄土高原丘陵沟壑区淤地坝的淤地拦沙效益分析［J］.农业工程学报，2003，19（6）：302－306.

［7］ 王光谦，薛海，李铁键.黄土高原沟坡重力侵蚀的理论模型［J］.应用基础与工程科学学报，2005，13（4）：335－344.

［8］ 于国强，李占斌，李鹏，等.黄土高原小流域重力侵蚀数值模拟［J］.农业工程学报，2009，25（12）：74－79.

［9］ 于国强，李占斌，张霞，等.黄土高原坡沟系统重力侵蚀数值模拟研究［J］.土壤学报，2010，47（5）：809－816.

［10］ 朱同新.黄土地区重力侵蚀发生的内部条件及地貌临界值分析［M］.北京：气象出版社，1987.

［11］ 陈浩.黄土丘陵沟壑区流域系统侵蚀与产沙关系［J］.地理学报，2000，55（3）：354－363.

［12］ 付凌.黄土高原典型流域淤地坝减沙减蚀作用研究［D］.南京：河海大学，2007.

［13］ 魏霞，李勋贵，李占斌，等.淤地坝对黄土高原坡沟系统重力侵蚀调控研究［J］西安建筑科技大学学报，2009，41（6）：856－861.

［14］ 雷阿林.坡沟系统土壤侵蚀链动力机制模拟试验研究［D］.陕西 杨凌：中国科学院水利部水土保持研究所，1996.

［15］ 黄自强.黄土高原地区淤地坝建设的地位及发展思路［J］.中国水利，2003（17）：8－11.

［16］ 郑宝明.黄土高原丘陵沟壑区淤地坝建设效益与存在问题［J］.水土保持通报，2003，23（6）：32－35.

［17］ 郑宝明，王晓，田永宏，等.淤地坝实验研究与实践［M］.郑州：黄河水利出版社，2003：152－367.

［18］ 黄正荣，梁精华.有限元强度折减法在边坡三维稳定分析中的应用［J］.工业建筑，2006，36（6）：59－64.

［19］ 赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24（3）：343－346.

［20］ 郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004，10，23（19）：3381－3388.

［21］ Zienkiewicz O C，Taylor，R L.The Finite Element Method［M］.New York：McGraw－Hill，1989.

［22］ Zienkiewicz O C，Humpeson C，Lewis R W.Associated and nonassociated visco－plasticity in soil mechanics.Geotechnique，1975，25（4）：671－689.

［23］ 吴海真，顾冲时.有限元强度折减法在土石坝边坡稳定分析中的应用［J］.水电能源科学，2006，24（4）：54－56.

［24］ 石长，赵新铭.用有限元强度折减法分析边坡稳定［J］.隧道建设，2006，26（3）：5－8.

［25］ 张彩双，李俊杰，胡军.有限元强度折减法的边坡稳定分析［J］.中国农村水利水电，2006（5）：72－74.

［26］ 王家臣.边坡工程随机分析原理［M］.北京：煤炭工业出版社，1996.

［27］ 祝玉学.边坡可靠性分析［M］.北京：冶金工业出版社，1993.

［28］ 龚晓南.土塑性力学［M］.2版.杭州：浙江大学出版社，1999.

［29］ 戚筱俊.工程地质及水文地质 ［M］.北京：中国水利水电出版社，1996.