交直流互联系统电压稳定性研究

，

(西南交通大学电气工程学院，四川 成都 610031)

0 引 言

直流系统由于不存在功角稳定问题，并且具有快速调节特性[1]，近来以高压和特高压直流输电为代表的交直流输电系统在中国电网中应用越来越多。相比交流系统，直流系统具有更多的参数和变量，并且其中应用大量的电力电子器件，使得交直流系统具有很强的非线性特性[2],在运行中换流器会消耗大量无功功率，逆变器吸收的无功功率约占直流输送功率的40%～60%，这对交流系统的容量提出非常高的要求[3]，使得系统电压稳定性面临严峻的挑战，需要深入研究影响系统电压稳定性的因素。

分岔理论是起源于力学失稳现象的一种理论[4]，1961年Andronov和Neimark第一次把分岔理论应用到电力系统的研究中，Harry G. Kwanty等人首次在对电压稳定性的研究中应用分岔理论。目前的分岔分析方法中大多以静态分析方法[6-7]为主。分岔理论能够更加精确地分析临界点附近系统的稳定性情况[9]。目前，利用分岔理论对交直流互联系统电压稳定性的研究还不是很深入，与交流系统相比，直流系统具有更多的动态元件和非线性环节[10]，为揭示电压失稳的机理，需要采用微分代数模型，进入深入研究。

选取更接近实际的交直流系统电压稳定性进行研究，使得出结论更具有可信度，通过连续潮流方法[11]得到系统PV曲线并求取系统霍普夫和鞍结分岔点，通过研究发现系统参数对电压稳定的影响作用，最后，通过时域仿真[11]的方法，观察整流侧和逆变侧电压在Hopf分岔点电压随时间的变化情况，得出影响交直流系统电压稳定的一些结论。

1 电力系统的系统模型

一般电力系统电压稳定性分析中，电力系统的模型可以表示为一组微分-代数方程组[5]。

(1)

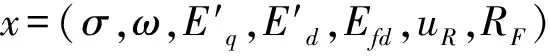
(2)

对上式进行变换得到系统的雅可比矩阵J=A-BD-1C，A=Dxf(x0，y0)，B=Dyf(x0，y0)，C=Dxg(x0，y0)，D=Dyg(x0，y0)，由分岔理论可知系统的稳定性完全由这个矩阵的特征值决定。

1.1 同步发电机的数学模型

同步发电机的运行特性在电力系统中起着举足轻重的作用,在对电力系统电压稳定性问题进行分析和研究的整个过程中，发电机是必须要考虑的因素之一。作为一种复杂的旋转设备，在发电机的建模中一般都应用随电机同步旋转的d-q坐标系，于是要首先对基于同步坐标x-y分量进行机网变换。针对不同的具体问题，发电机根据转子绕组数的不同采用不同的模型。这里采用IEEE双轴4阶模型，主要考虑转子绕组的暂态过程而忽略次暂态过程和定子绕组暂态过程，同时考虑g绕组、f绕组暂态和转子运动的动态。发电机实用4阶模型[10]如下。

(3)

式中，i取值由1至发电机总数；j为与节点i相连的节点号；δ1为第i台发电机功角；θij为节点i和节点j之间的电压相角差；gij和bij为节点i和节点j之间的电导和电纳。

1.2 励磁系统数学模型

励磁系统的动态特性对系统稳定有着重要的影响，通过励磁电流的调节从而调节无功输出，达到稳定发电机机端电压的目的，这里采用励磁器——IEEE DCⅠ型励磁器，数学模型采用文献[12]提出的一阶模型。

(4)

式中，TA和KA分别为励磁调节器的时间常数和放大倍数；uref为励磁参考电压。

1.3 直流系统数学模型

直流系统数学模型一般分为稳态模型、准稳态模型和暂态模型[13]，这里研究小扰动情况下交直流系统的电压稳定性，考虑到直流换流器控制方式的动态行为，直流系统采用准稳态模型。

由于直流线路的两端一般都与交流系统相连接，一端通过整流器把交流变为直流，另外一端通过逆变器把直流变为交流，如图1所示。

图1 直流系统结构图

整流器和逆变器原理基本相同，所以统称为换流器，其数学模型如下[2,14]。

(5)

式中，kT和θd分别为换流变压器变比和换流器的控制角，最后两个公式说明换流器的控制方式，这里主要研究的是整流器定电流逆变器定熄弧角这种控制方式；K1和Kp分别为积分放大倍数和比例放大倍数。

考虑到直流线路和控制器的动态过程，直流线路采用L-R等值电路，忽略对地充电电容，微分方程[15]为

(6)

式中，Udrec和Udinv分别代表整流侧和逆变侧直流电压；Rd为直流线路电阻。

1.4 系统网络模型

发电机节点的潮流方程[16]为

(7)

非发电机节点潮流方程为

(8)

式中，l为非发电机节点号；k为与l相关联节点号；Pl和Ql为节点l的负荷给定的有功和无功功率。

直流节点的潮流方程为

(9)

式中，r为直流节点；s为与直流节点相关联的交流节点；第一个方程中正号表示整流器端，负号表示逆变器端。

2 分析理论

2.1 分析理论

在电力系统电压稳定性分析中根据所考虑的动态特性变化范围的不同，分岔可以分为局部分岔和全局分岔[20]。局部分岔是单独研究平衡点的某一邻域内向量场的分岔，常见的有：鞍结分岔、奇异诱导分岔、霍普夫分岔、极限诱导分岔。这里主要针对交直流系统在霍普夫分岔和鞍结分岔时系统电压稳定特性进行研究。

(1)霍普夫(Hopf)分岔[17]

通过选择可控的系统参数在不断变化的过程中，系统雅可比矩阵的一对共轭特征值从左向右或是从右向左穿越虚轴，系统发生霍普夫分岔。其中又分为超临界和亚临界霍普夫分岔。

(2)鞍结分岔(SNB)[17]

系统初始运行时一般至少有2个平衡点，随着控制参数的不断变化，相应平衡点也会沿着系统PV曲线相互靠近，当系统参数到达一定临界值时，两个平衡点会合并为一个，此时发生SNB分岔，对应系统特征方程有一个零特征值。

2.2 连续潮流法(延拓法)

连续潮流法是对电力系统电压稳定性分析的有力工具，在对交直流系统电压稳定性分析研究中应用连续潮流方法[11]追踪系统的平衡解流形并求取分岔点，这种方法可以避免在临界点常规潮流方程难以收敛的问题。连续潮流法包含4个步骤：预估、校正、步长控制和参数化[9]。此方法的基本思想就是从初始运行点开始，随着控制参数的不断变化，通过对下一运行点进行预估、校正，直至绘制出完整的系统PV曲线。

在分析中，一般将系统变量x、y统一用z表示。x、y的维数分别为p、q，n=p+q，系统的平衡解流形Φ可以表示为

Φ={zRn+1/F(z)=0}

(11)

① 预估[5]

初始的3个点用切向量法进行追踪，启动算法，其切向量通过下式求解为

(12)

从第4个点开始，采用切线加割线的方法[9]进行追踪，切向量采用下面方法进行求解[5]。

JP=

其中，p=1,2,…,n+1。

V=[J1，J2…Jn+1]T，τ=V/‖V‖,即为平衡解流形Φ的单位切向量。

② 校正及参数化[5]

对初值进行校正采用的是垂直法校正，然后对预估值进行修正得到准确值，修正表达式为

(13)

通过牛顿迭代法求解上述方程组，直到得到准确解。

③步长控制

在算法的实现过程中，步长选择是一个重要因素：如果步长太大，会导致曲线不精确；步长太小，虽然计算结果精确，但是计算量过大。实时根据曲线形状调整步长大小成为不错的选择，这里采用如下步长控制方法[19]为

h=h0/‖τ‖

(14)

式中，‖τ‖为切向量的2-范数或∞-范数；h0为初始设定的一个标量。

2.3 单参数分岔点的求解方法

单参数分岔点的求解方法主要有延拓法和直接法。延拓法[19]利用连续潮流法追踪系统的平衡解流形得到PV曲线，过程中利用雅可比矩阵特征值的变化情况检查是否满足各种分岔发生的条件、判断PV曲线上是否存在相应的分岔点。直接法就是用牛顿拉夫逊法直接求解各种分岔点所满足的分岔条件和平衡解条件的非线性代数方程组[11]。

直接法求霍普夫分岔点的迭代方程组为

(15)

式中，v为未知变量；v0为已知列向量；J=A-BD-1C，(x,y,v,ω)为上述方程的未知数。

直接法求鞍结分岔点的迭代方程

(16)

2.4 时域仿真法

电力系统电压失稳实质上是一个动态发展过程，时域仿真法就是考虑系统的非线性和元件的动态特性的影响，利用数值积分的方法得到电压等状态量随时间变化的曲线。这里采用联立求解法[14]，利用隐式梯形法对微分方程进行求解，基本思想为：用隐式梯形法将微分方程转化为差分型代数方程，然后与代数方程组联立，最后用牛顿拉夫逊法解此非线性方程组。

隐式梯形法的计算方法为

(17)

3 电压稳定性研究

研究选取交直流系统是在WSCC9节点系统的基础上稍加改造，将节点7和8之间的交流线路换成直流线路,如图2。与发电机1相连节点定为参考节点，参数见文献[12]直流线路，电抗为0.025 p.u.，额定功率为67.2 MW,额定电压为56 kV,额定电流为1.2 kA,初始触发角和熄弧角分别为18°和20°，系统基准额定功率为100 MW，直流电流和电压都去额定值下的参考值。

对交直流系统电压稳定性的研究是在基于Matlab仿真基础上进行的，通过M文件编程实现系统模型建立，并应用前文所提到的算法求取系统的PV曲线，系统参数都用标幺值表示,对于不同参数表现出的不同系统特性进行仿真实验，从而发现问题。选择与1节点相连的发电机1的有功功率P作为系统的控制参数。

图2 WSCC9节点交直流系统

3.1 系统参数对电压稳定性的影响

图3 Idref取不同值时系统P-U7曲线

图3中，◇代表Hopf分岔，○代表SNB分岔，通过大量的仿真实验发现，系统在发生SNB分岔之前一般会先发生Hopf分岔[5]，通过对分岔点的时域仿真曲线可以看出，系统在Hopf分岔点处会发生振荡失稳，所以Hopf分岔点处的功率即为系统的传输功率极限[15]。图3中Idref为系统直流电流的参考值，可以看出随Idref的增大Hopf分岔点依次发生延迟，传输功率逐渐增大，但是，系统的电压水平降低，这是由于Idref较小时，直流系统对交流系统的无功需求比较小，而且能够降低换相失败的可能性[2]。

从图4可以看出，当Vref为0.89时，此时即使系统负荷比较轻的情况下，系统还是会比较早的就发生Hopf分岔，说明此时系统非常不稳定；当Vref为1.5时，这时系统在发生SNB分岔之前不再发生Hopf分岔现象，可以看出随着Vref的不断增大，系统分岔点不断右移，说明选取比较高的Vref不仅可以提高系统的传输功率极限，而且还可以消除Hopf分岔点，从而避免系统发生振荡失稳[21]。

3.2 直流输电线路对电压稳定性的影响研究

针对所选WSCC9交直流系统，换流器控制方式选择定电流定熄弧角(CC/CEA)，在感应电动机负荷下，应用时域仿真法观察整流侧和逆变侧电压在Hopf分岔点处受到扰动后，电压随时间的变化情况。

图5 节点7直流电压的时域仿真曲线

图6 节点8直流电压的时域仿真曲线

对比图5和图6可以看出，在Hopf分岔点处受到相同大小的扰动，逆变侧节点电压U7做非等幅振荡，并且有明显的畸变，而整流侧节点电压U8做等幅振荡，这说明了直流系统对两端的影响程度不相同，这是因为换流设备在扰动发生后快速作用，通过调节阀的触发角，改变潮流和电压的大小，逆变侧由于功率的传输要经过直流线路和换流设备，所以受直流系统的影响比较大，逆变侧电压会出现。

4 结 论

通过对发电机、励磁系统和交直流系统网络进行建模，并考虑交直流系统中换流器及其控制方式等动态变化规律，运用分岔分析方法，通过连续潮流方法追踪系统平衡解流形，并求取霍普夫分岔和鞍结分岔。增大系统直流的参考值可以延迟系统Hopf分岔但是以降低系统电压水平为代价的，所以在应用中应注意权衡；并不是所有情况下系统都会发生Hopf分岔，当励磁系统参考电压比较大时，系统只发生SNB分岔，此时SNB分岔点作为系统传输功率极限点，并且采用较高的励磁系统参考电压可以避免系统发生振荡失稳。最后通过时域仿真的方法发现，直流系统对两端交流节点电压的影响并不相同，逆变侧由于受直流系统影响比较大，会出现电压畸变现象。

[1] 刘明波，程劲辉，程莹.交直流并联电力系统动态电压稳定性分析[J].IEEE Transactoins on Power Delivery,1998，13(13)：923-931.

[2] 徐政.交直流电力系统动态行为分析[M].北京：机械工业出版社，2004.

[3] 庄慧敏.基于分岔理论的交直流电力系统电压稳定性分析方法研究[D].成都：西南交通大学，2009.

[4] 刘彩霞，周艳平.分岔理论在电力系统电压稳定性中的应用[J].云南水利发电，2007,23(3):87-90.

[5] 彭志炜，胡国根，韩祯祥.基于分岔理论的电力系统电压稳定性分析[M].北京：中国电力出版社，2005.

[6] 刘崇茹,张伯明.交直流混合输电系统灵敏度分析[J].电力系统自动化,2007,31(12):45-49.

[7] 邱革非,束洪春,董俊,等.联于弱交流系统的HVDC输电系统输电能力和电压稳定性的研究[J].昆明理工大学学报，2005,30(3):50-55.

[8] 庄慧敏，肖剑.交直流系统电压稳定性的Hopf分岔分析[J].高电压技术，2009,35(3):699-704.

[9] 李康.基于分岔理论的电力系统动态电压稳定性分析[D].成都：西南交通大学，2012.

[10] S.L.Richer,R.A.Decarlo.Continuation Methods:Theoryand Application[J].IEEE Transations on Circuits and Systems,1983,13(4):459-463.

[11] 顾伟.电力系统最优分岔控制研究[D].南京:东南大学,2006.

[12] 樊纪超.交直流并联输电系统动态安全域及其割集表示[D].天津:天津大学,2005.

[13] 王锡凡,方万良,杜正春.现代电力系统分析[M].北京:科学出版社,2003.

[14] 谭涛亮,张尧.交直流互联系统动态电压稳定的分岔值分析[J].电网技术,2011,35(3):49-56.

[15] 李宏仲.基于Hopf分岔理论的电力系统动态电压稳定研究[D].上海:上海交通大学,2008.

[16] 赵兴勇,张秀彬,苏小琳.电力系统电压稳定性研究与分岔理论[J].电工技术学报,2008,23(2):87-95.

[17] X.Yang,Y.chen,H.L.Shu. Stability Analysis of AC/DC Power Transmission System based on Bifurcation Theories[C].Sustainable Power Generation and Supply,Nanjing,2009:1-7.