基于GA-RBF网络的磷酸铁锂电池SOC预测研究

黄智宇，曹玉恒

(重庆邮电大学重庆高校汽车电子与嵌入式系统工程研究中心，重庆400065)

0 引言

能源问题使得建立清洁可再生的新能源体系成为人类社会发展的必然选择。中国是汽车消费和生产大国，正面临着节能减排的重大挑战［1］。动力电池是制约电动汽车发展的关键，而磷酸铁锂(LiFe－PO4)电池因其寿命长、安全性能好、成本低、无记忆性等特点成为电动汽车的理想动力源［2］。

在电动汽车的发展过程中，动力电池荷电状态(state－of－charge，SOC)是电池的一个重要参数，用来表示电池的剩余电量，是对动力电池的使用进行必要管理和控制的主要依据［3］。同时SOC预测也是动力电池管理系统的主要功能之一，根据SOC来估计续驶里程，在电池充放电时依靠SOC做出相应的控制，防止动力电池因过充放电造成其本身损害甚至危险的发生［4］。因此，如何准确预测SOC成为电动汽车发展的重要环节。

目前，LiFePO4电池SOC预测方法主要有基于列文伯格－马夸尔特 (levenberg－marquardt，LM)算法优化反向传播 (back propagation，BP)神经网络法［2］、遗传算法(genetic algorithm，GA)优化 BP 神经网络法［5］、电化学模型法［6］、径向基(radial basis function，RBF)神经网络法［7］等，其中 RBF 神经网络法的优势主要在于预测精度要高于其他预测方法，而且运行稳定。相对于粒子群优化算法(particle swarm optimizer，PSO)，遗传算法具有收敛快、适用于离散问题等优点。GA与RBF神经网络的结合可以克服网络参数选择的随机性，使网络具有更好的精度和适应能力。因此本文提出用GA－RBF网络法进行SOC预测，为新能源汽车的电池管理系统设计与优化提供新的思路。

1 SOC估算方法的选择

1.1 SOC估算方法

由于电池的SOC与很多因素相关(如温度、极化效应、电池寿命等)，而且具有很强的非线性，若要提高SOC估算的精度，需要在测量方法、电池模型和估算算法等方面进行深入研究。国内外普遍采用的方法［5］有:放电试验法、安时法、开路电压法、内阻法、卡尔曼滤波法、线性模型法和神经网络法等。

1.2 SOC现有估算方法存在的缺陷

目前SOC估算有多种方法，但各种估算方法都存在某个方面的缺陷。

1)放电试验法要求电池处于恒流放电状态，而且需要花费大量测量时间;

2)安时法易受到电流测量精度的影响，在高温或电流波动剧烈情况下精度很差;

3)开路电压法进行电池SOC估计时，电池必须静置较长时间以达到稳定状态，而且只适用于电池电流非剧烈变化状态下的SOC估计，不能满足在线检测的要求;

4)内阻法需要精确测量电池的内阻，一般电池内阻在毫欧级，对测量仪器的要求非常高，难以在实际中加以应用;

5)卡尔曼滤波法是目前采用较多的一种估算方法，它对电池模型依赖性较强，要获得准确的SOC，需要建立较为准确的电池模型，而电池模型的准确程度和复杂度是成正比的;

6)线性模型大致分为等效电路模型和简化电化学模型。等效电路模型多采用较简单的Thevein模型，而如果采用更为复杂的电路模型，模型参数的辨识和状态方程的建立都将是很大的挑战。由于模型的简化，并不能充分反映电池的内部规律，会造成较大的估计误差。

1.3 本文的SOC预测方法

RBF神经网络法有很强的非线性拟合能力，可映射任意复杂的非线性关系，具有很强的鲁棒性和记忆能力，且学习规则简单、学习能力强大，便于计算机实现。但如何合理确定网络的结构和参数，目前尚未有系统的规律可循，网络的逼近性能因此受到影响。

GA借鉴了自然界遗传中适者生存法则，在问题空间进行全局并行、随机的搜索优化，使得种群全局最优的收敛。与传统算法相比，GA训练神经网络无需先验知识，而且对初始参数不敏感，不会陷入局部最小点。所以具有全局搜索能力的GA可以对RBF神经网络进行优化，寻找到最优的网络结构和参数，以保证最佳的网络性能。

因此，本文提出一种基于GA－RBF神经网络的SOC估算方法，用于预测在不同放电电流和不同电压下的LiFePO4电池SOC值。此方法克服了网络参数选择的随机性，具有更好的精度和适应能力。

2 基于GA-RBF网络SOC预测模型建立

2.1 RBF 神经网络

建立一个三层的RBF神经网络，并将电池的电压(V)、电流(A)作为输入量，SOC值作为输出量，如图1所示。

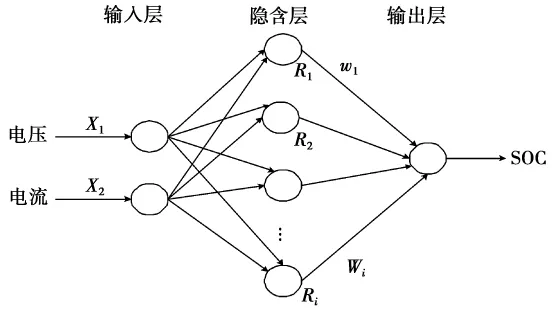
图1 基于GA－RBF神经网络的SOC预测模型Fig.1 Based on GA－RBF neural network of SOC prediction model

RBF神经网络的隐含层空间起到非线性转换作用，网络的实现从输入层到隐含层是非线性映射，而从隐含层到输出层是线性映射。其中隐含层节点中实现非线性映射的作用函数(基函数)采用的是高斯函数

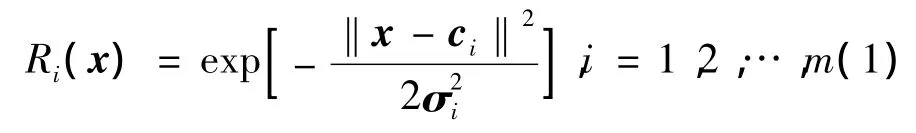
(1)式中:x是n维输入向量;ci是第i个基函数的中心，与x具有相同维数的向量;σi是第i个感知的变量，它决定了该基函数围绕中心点的宽度;m是感知单元个数。模型中将电池的电压和电流作为神经网络的输入，所以输入x是二维向量。

从图1可以看出，输入层实现从x到Ri(x)的非线性映射，输出层实现从Ri(x)到SOC的线性映射，因此通过GA－RBF神经网络预测的电池SOC值为

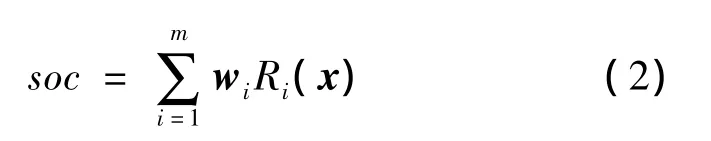
(2)式中，w是网络权值。

利用Matlab工具箱里的newrb函数来创建神经网络，如式(3)所示

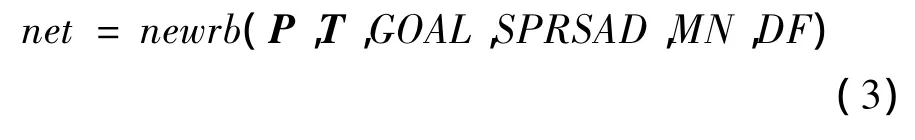
(3)式中:P为输入矢量;T为输出矢量;GOAL为均方误差目标;SPRSAD为径向基函数的扩展速度;MN为神经元最大的数目;DF为2次显示之间所添加的神经元数目。本文中P为电流和电压参数矩阵，T 为SOC 预测值，GOAL设置为0.000 5，SPRSAD值的选取对RBF神经元输入向量覆盖区间的影响很大，所以需要不同的SPRSAD值进行尝试，以确定一个最优值。

2.2 GA-RBF 算法设计

将GA与RBF网络相结合，就是将GA的全局寻优能力与RBF网络的非线性逼近能力较好地结合起来。通过GA找出RBF网络的3个参数(宽度向量σ，中心矢量c和网络权值w)的最优值，从而得到最优的网络结构，然后用这个网络结构进行SOC预测。基于GA－RBF神经网络预测SOC算法包括编码、确定初始种群、适应度值评价检测、选择、交叉、变异以及终止条件判断7个步骤。

1)编码:将需要进行优化的径向基模型的宽度向量σ，中心矢量c和网络权值w进行二进制排列编码，编码长度与精度有关，编码越长精度越高［8］，但是编码过长会使遗传算法的搜索空间急剧扩大，所以设定每个参数的编码长度为10。

2)确定初始种群:设定初始群体大小为G，进化代数为Size。

3)适应度值评价检测:适应度函数表明个体或解的优劣性[9]。适应度较高的个体遗传到下一代的概率就相对较大［10］。本文是将电池的电流和电压作为输入，预测SOC，输出的SOC越接近真实值越好，所以将预测输出和期望输出之间的误差绝对值平方和倒数作为适应度函数

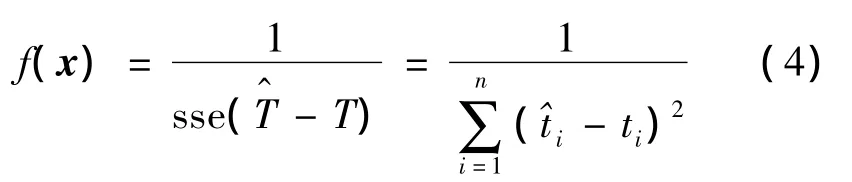
4)选择:选择的目的是为了从当前群体中选出优良的个体，使他们有机会作为父代繁殖下一代［11］。选择操作采用轮盘赌法从种群中选择适应度好的个体组成新种群。

5)交叉:使用单点交叉算子。只有一个交叉点位置，任意挑选经过选择操作后种群中2个个体作为交叉对象，随机产生一个交叉点位置，然后按照交叉概率Pc再进行部分基因交换［12］。

6)变异:采用基本位变异，在变异概率Pm指定变异点进行取反运算，从而产生出新一代的个体。

7)终止条件判断:若 t≤Size，则 t←t+1，转到步骤2);若t＞Size，则以进化过程中所得到的具有最大适应度的个体作为最优解输出，终止运算。

3 仿真与结果分析

3.1 电池数据库的建立

以某厂家提供的LiFePO4(3.2 V，50 Ah)电池为测试对象，在新威尔公司提供的动力电池性能测试设备上进行测试，由与其连接的上位机保存及读取数据。

室温为25℃时，在不同的恒定电流条件下进行电池测试，将电池分别按照0.2 C，0.5 C，1 C，2 C的放电倍率下进行放电测试，在测试过程中上位机可以自动记录电池的各个参数(电流、电压、放电容量)的变化，采样频率为1 Hz。从中取出400组数据，并将数据分为训练样本和测试样本。其中训练样本40组，测试样本360组，如表1所示。

3.2 模型训练

利用Matlab神经网络工具箱的newrb函数进行基于GA－RBF神经网络模型的搭建与训练。种群规模通常取10－100，求解问题的非线性越大，规模的选择就应该越大［13］。训练过程中发现，在进化代数100步后误差基本不变。因此，遗传算法参数设置为:种群规模G=10，进化代数Size=100，变异概率Pm=0.1，交叉概率Pc=0.4，将归一标准化处理后的训练样本数据输入网络。GA－RBF神经网络误差曲线如图2所示。

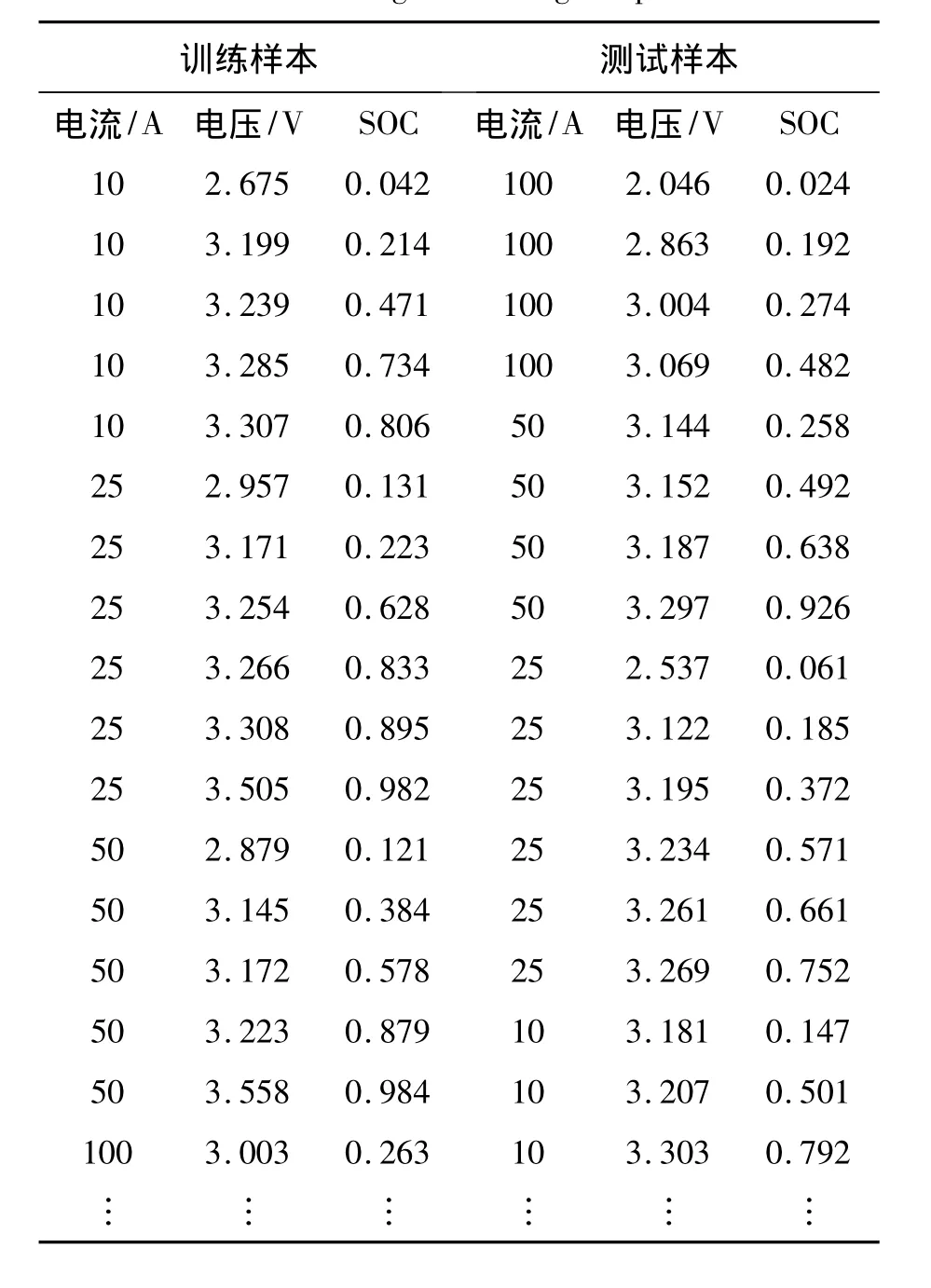
表1 训练与测试样本数据Tab.1 Training and testing sample data

图2 GA－RBF神经网络误差曲线Fig.2 Error curve of GA－RBF neural network

图2中，直线表示目标误差，曲线表示训练误差，训练过程中，在65步时达到了精度(0.000 5)要求，比采用LM算法优化神经网络法和RBF神经网络法的预测精度(0.001)提高了两倍。表明基于GA－RBF神经网络SOC预测具有较高的准确性。

3.3 结果分析

为了验证基于GA－RBF神经网络对SOC预测的准确性，并优于RBF神经网络对LiFePO4电池SOC的预测。将测试样本分别输入经过训练的GARBF神经网络和未优化的RBF神经网络，其仿真结果如图3所示。放电电压与SOC关系曲线如图4所示。

图3 预测值与目标值对比曲线Fig.3 Contrast curve between predicted value and target value

图3、图4中虚线表示目标值，图3a中实线表示RBF预测值，图3b和图4中实线表示GA－RBF预测值。对图3a和图3b进行对比，可以看出仿真得到的GA－RBF预测值比RBF预值更接近目标值，尤其在电压2.7～3.4 V之间最为显著。从图4中更能清晰的看出GA优化后的RBF神经网络预测LiFePO4电池SOC具有较高的准确性和鲁棒性。

图4 放电电压与SOC关系曲线Fig.4 Relationship carve between discharge voltage and SOC

图5所示为Matlab仿真过程中的网络输出误差曲线图，其中实线是RBF预测误差曲线。

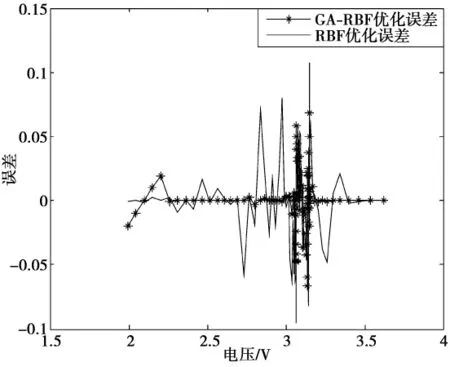
图5 网络输出误差Fig.5 Network output error

从图5可以看到在电压2.4～3.5 V之间，GARBF预测误差在2%左右，对SOC估算误差大部分满足5%的技术指标。而RBF神经网络SOC估算误差较大，最大时到达了10%。通过仿真实验证明，优化后的RBF神经网络对SOC的估算能力比优化前的更好，精度更高。

4 结束语

本文建立了基于GA－RBF的神经网络模型，通过GA优化RBF网络模型中的宽度向量σ、中心矢量c和网络权值w 3个参数的算法，对LiFePO4动力电池SOC进行预测研究。并进行了仿真实验，实验结果表明，基于GA－RBF神经网络SOC预测方法具有较强的可行性，比RBF神经网络预测结果更加准确，满足电池管理系统对LiFePO4动力电池SOC预测的精度要求。同时，GA－RBF神经网络结构简单，具有较好的泛化性能，具有较高的理论价值，并对实际工程应用具有较高的指导意义。

［1］LEE S，KIM J，LEE J.State－of－charge and capacity estimation of lithium－ion battery using a new open－circuit voltage versus state－of－charge ［J］.Journal of Power Sources，2008，2(185):1367－1373.

［2］尹安东，张万兴.基于神经网络的磷酸铁锂电池SOC预测研究［J］.电子测量与仪器学报，2011，25(5):433－437.YIN Andong，ZHANG Wanxing.Research on estimation for SOC of LiFePO4 Li－ion battery based on neural network［J］.Electronic measurement and instrument journal，2011，25(5):433－437.

［3］赵淑红，吴峰，王子冬.磷酸铁锂动力电池工况循环性能研究［J］.电子元件与材料，2009，28(11):43－47.ZHAO Shuhong，WU Feng，WANG Zidong.Study on operating mode cycle performance of lithium ion power battery with natural graphite and LiFePO4［J］.Electronic Components ＆Materials，2009，28(11):43－47

［4］PILLER S，PERRIN M.Methods for state－of－charge determination and their applications［J］.Journal of Power Sources，2001，12(96):113－120.

［5］ZHAO Yongqin，SUN Jinlei，WANG Xudong.Power Battery Charging State－of－Charge Prediction based on Genetic Neural Network［J］.International conference on information，electronic and computer science(ICIECS)，2010，4(6):1－4.

［6］LI X， XIAO M， MALINOWSKI K.State－of－charge(SOC)estimation based on reduced order of electrochemical model for a pouch type high power Li－polymer battery［J］.Vehicle Power and Propulsion Conference(VPPC)，IEEE，2011，19(6):1－6.

［7］ZHOU Yongqin，ZHANG Yanming，ZHAO Pengshu.Study of Battery State－aI－charge Estimation for Hybrid E－lectric Vehicles［J］.Strategic Technology(IFOST)，2011，8(1):287－290.

［8］王海军，乔烨.基于GA－RBF模型的无线电波信号预测研究［J］.研究设计，2011，27(12):13－14.WANG Haijun，QIAO Ye.The prediction research of Radio signal based on the GA－RBF model［J］.research ＆design，2011，27(12):13－14.

［9］马凯，何志琴.基于遗传算法和神经网络的复杂对象的建模与优化术［J］.组合机床与自动化加 工技术，2012，1(1):32－36.MA Kai，HE Zhiqin.Modeling and Optimization of Com－plex Objects Based on Genetic Algorithm and Neural Network［J］.Modular Machine Tool ＆ Automatic Manufacturing Technique，2012，1(1):32－36.

［10］姚雪梅，夏东伟，李建.基于GA－RBF神经网络的光伏电池 MPPT研究［J］.青岛大学学报:工程技术版，2009，24(2):10－14.YAO Xuemei，XIA Dongwei，LI jian.Research of Maximum Power Point Based on GA－RBF Neural Network［J］.Journal of Qingdao Technological University:engineering＆ technology edition，2009，24(2):10－14.

［11］CAO Zhengcai，ZHAO Yingtao，FU Yili.Research on point stabilization of a wheeled mobile robot using fuzzy control optimized by GA［J］.China universities of posts and telecommunications:English edition，2011，18(5):108－113.

［12］蒋建平，阎长虹，高广运.地基土压缩系数的RBF神经网络预测［J］.江苏大学学报:自然科学版，2011，32(2):232－152.JIANG Jianping，YAN Changhong，GAO Guangyun.Prediction on compressibility coefficient of soil based on RBF neural network［J］.Journal of Jiangsu University:natural science edition，2011，32(2):232－152.

［13］GUO Pengfei，WANG Xuezhi，HAN Yingshi.The enhanced genetic algorithms for the optimization design［J］.Biomedical Engineering and Informatics(BMEI)，2010，3(7):2990－2994.