Laasraoui-Jonas位错密度模型结合元胞自动机模拟AZ31镁合金动态再结晶
刘 筱 ,朱必武 ,李落星
(1.湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082;2.湖南大学 机械与运载工程学院,长沙 410082)
镁合金因密度小、比强度高和比刚度高等优点,在汽车、航空和电子等领域得到广泛的应用[1-3]。但是,制约变形镁合金发展的主要原因在于其较差的室温塑性变形能力,如何在较大程度上改善镁合金的塑性已成为人们关注的焦点。改善的方法主要包括合金化和晶粒细化等[4],晶粒细化的方法主要有动态再结晶、快速凝固、喷射沉积、强应变塑性变形等。镁合金是低层错能金属,与铝等高层错能金属相比,镁合金在热变形过程中发生动态再结晶[5]。所以,镁合金动态再结晶组织的模拟和预测已经成为镁合金热加工数值模拟技术的研究重点。
再结晶的驱动力来至于变形过程中的位错密度的消散[6]。从而,选择适合 AZ31镁合金的位错密度模型对再结晶过程的模拟起到很重要的作用。目前,模拟材料内部位错密度变化的模型包括修正的L-J位错密度模型、KM位错密度模型、两个参数位错密度模型和多参数位错密度模型等。KM 位错密度模型的主要特征是材料的变形机制由总的位错密度决定;两个参数模型具有KM模型的特征,但是将总的位错密度分成了迁移的位错密度和积累位错密度;多参数位错密度模型则考虑了亚晶粒尺寸的影响[7]。修正的 L-J位错密度模型不仅仅具有KM位错密度模型的特征,同时考虑了晶界迁移对位错演变的影响。
本文作者通过热模拟实验得到AZ31镁合金流变应力曲线,根据流变应力曲线的图形转换得到硬化率曲线,/θσ∂∂—σ曲线,曲线,最终得到不同应变速率下lnr—1/T的曲线,表明回复参数在不同应变速率下的自然对数与温度的倒数具有线性相关的关系,并且斜率基本相同,证实了修正的L-J位错密度模型适用于AZ31镁合金动态再结晶过程中位错密度的计算,采用修正的L-J位错密度模型结合CA方法模拟的AZ31镁合金的动态再结晶结果与实验结果相似。
1 实验
实验为了保证所有的镁合金样品晶体取向保持一致(即是所有的样品具有相同初始条件),采用 AZ31挤压态镁合金,成分(质量分数,%)为Al 2.8~3.2,Mn 0.2~1.0,Zn 0.8~1.2, Si不大于 0.05,Cu 不大于 0.05,Ni不大于0.005,Fe不大于0.005,杂质不大于0.3,余量为 Mg。沿挤压棒的长度方向在中心截取直径为10 mm,高为12 mm的圆柱体试样,在Gleeble-3500热模拟试验机进行等温压缩变形实验,预设温度为300~500 ℃、应变速率为 0.03~3 s-1,真应变为 1,并获取流变应力曲线。采用LeitZ-MM-6卧式金相显微镜观察合金压缩后的显微组织。
2 动态再结晶模型
2.1 位错密度模型
动态再结晶过程是一个加工硬化、动态回复和再结晶的过程。这些过程导致位错密度的变化,既是加工硬化导致位错的堆积,动态回复和再结晶导致位错的消散,最终体现流变应力的变化[6,8-10]。
Laasraoui-Jonas(L-J)位错密度模型(见式(1))表达了位错密度在晶粒内的演变。流变应力与位错密度的关系见式(2)。

式中:ρ表示位错密度;ε表示应变增量;h表示硬化参数;r表示回复参数;α表示泰勒因子,一般为0.5;μ表示剪切模量;σ表示的流变应力。
根据式(1)和(2)可知,位错密度的变化体现了材料的微观变化,流变应力体现的是材料的宏观变化,同时流变应力是依赖位错密度的变化。
再结晶过程也是一个形核和长大过程,晶粒长大过程中的晶界迁移会造成位错的消散,GOURDET和MONTHEILLET[11]采用修正的L-J位错密度模型(见式(3))其考虑了温度和应变速率的影响,其中回复参数表示如式(4)。
式中:dV表示晶界迁移扫过的体积;ε˙表示应变速率;0ε˙表示应变速率校准常数;m1是常数;Qb是自扩散激活能;R是摩尔气体常数;T是绝对温度。
2.2 形核和长大模型
金属在一定再结晶温度以上变形,短时间内发生回复,长时间加热,发生再结晶。再结晶新晶粒的形成是形核和长大的两个基本过程[12]。
2.2.1 形核模型
XIAO等[13]根据实验和理论分析,提出动态再结晶形核速率不仅仅与温度和应变速率有关,同时也与应变量有关(见式(5))。
式中:n˙表示的形核率;C、m、p为常数;Z是Zenner-Hollomon参数;cε是临界应变。
2.2.2 长大模型
当位错密度和应变达到临界值时,开始发生再结晶,即有新晶粒的生长。DING和 GUO[7]、CHEN等[8]以及李落星等[14]采用式(6)表达新晶粒生长速度(vi)。

式中:M表示边界迁移(见式(7));Fi表示第i个新晶粒驱动力(见式(8));ri表示晶粒半径。
式中:δ为晶粒边界厚度;b为柏氏矢量;Db表示边界自扩散有效系数;K为波尔赫兹常数;ρm表示母相的位错密度;ρi表示第i个新晶粒的位错密度;γi表示晶界能;τ是位错线能量。
3 结果和分析
3.1 流变应力曲线
图1所示为AZ31镁合金应变速率为0.03、0.3和3 s-1下温度为300、350、400、450和500 ℃、真应变为1时的流变应力曲线。流变应力曲线表现出很明显的单峰值,是典型的连续动态再结晶,那么在相对高的应变速率和相对低的温度下晶粒尺寸随着应变的增加而减小[15-16]。图1(c)显示应变速率为3 s-1、温度为300 ℃和 350 ℃时的流变应力曲线从应变量为 0.007开始产生了反C曲线,说明发生了孪生,所以在这种条件下不能采用修正的L-J位错密度模型进行微观组织模拟。
3.2 硬化率曲线
式(9)、(10)、(11)中:C1表示常数;σ0为屈服应力。
图4所示为根据式(11)求解的斜率(r)。式(4)表明,如果式(3)适用于材料动态再结晶过程中位错密度的演变的计算那么不同应变速率下的回复参数r的自然对数与温度的倒数 1/T成线性相关关系并且斜率相似,从而图5表明修正的L-J位错密度模型(式(3))适用于AZ31镁合金动态再结晶过程中的位错密度演变的计算。

图1 相同应变速率下不同温度的流变应力曲线Fig.1 Flow stress curves under different temperatures and strain rates: (a)ε˙=0.03 s-1; (b)ε˙=0.3 s-1; (c)ε˙=3 s-1
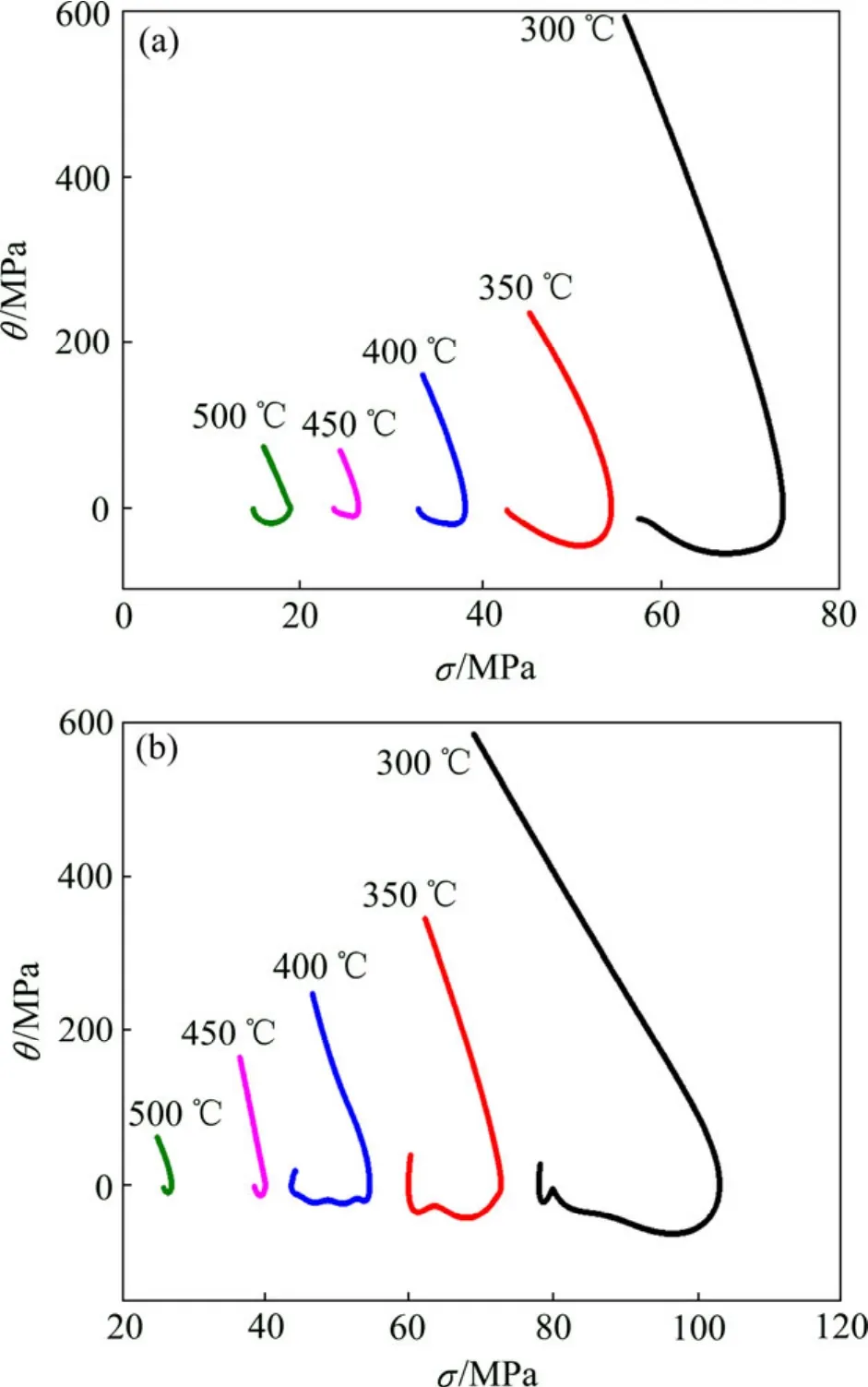
图2 相同应变速率下不同温度的硬化率曲线Fig.2 Work hardening rate curves at different temperatures:(a)ε˙=0.03 s-1; (b)ε=3 s-1
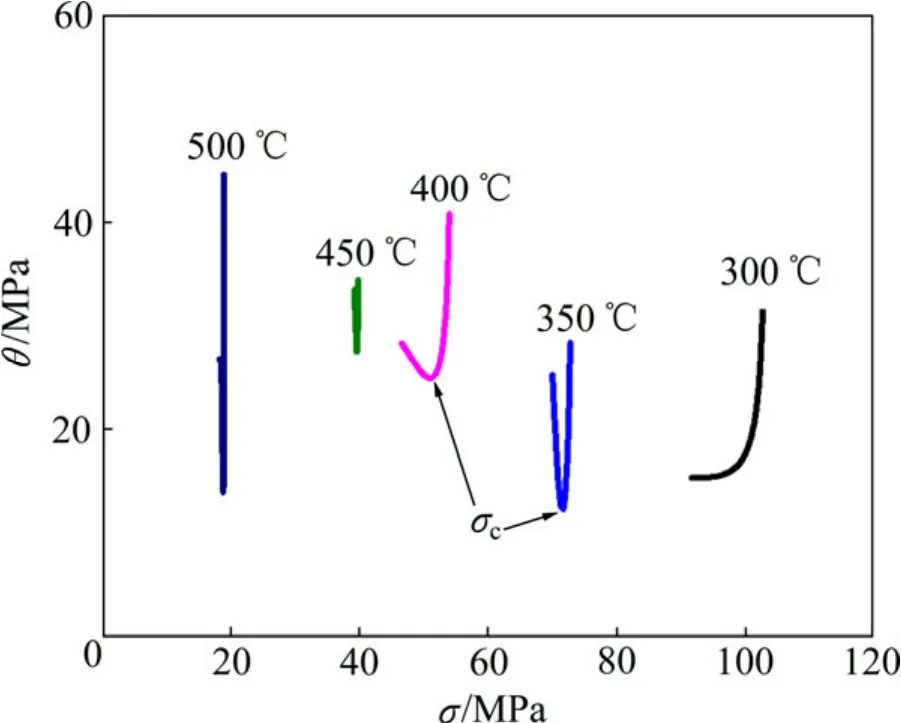
图3 应变速率为 0.3 s-1时不同温度下的流变应力基于θ=-∂θ/∂σ 的曲线Fig.3 Flow stress dependence of θ=-∂θ/∂σ at strain rate of 0.3 s-1 and different temperatures
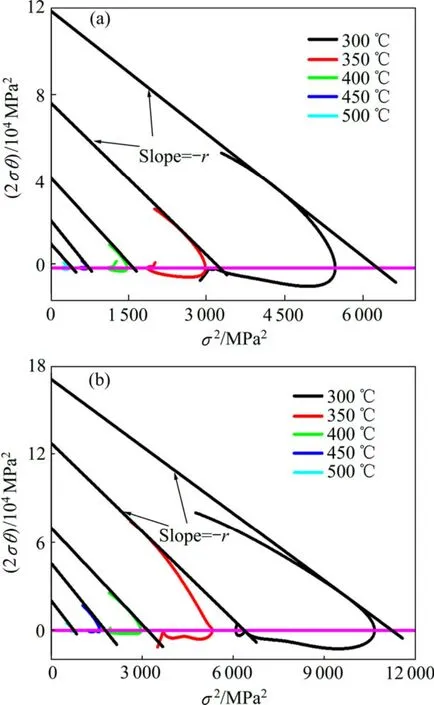
图4 2σθ与 σ2关系曲线Fig.4 Relationship curves between 2σθ and σ2: (a)ε= 0.03 s-1;(b)ε=0.3 s-1
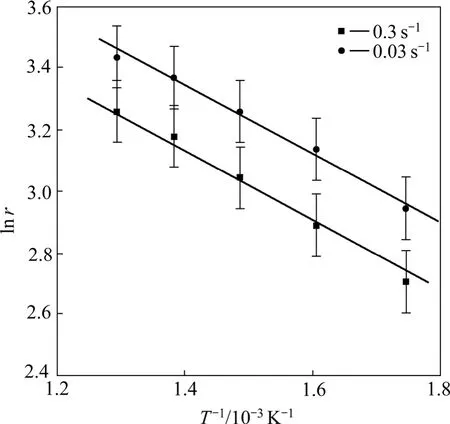
图5 ln r —1/T的关系曲线Fig.5 Relationship curves between ln r and 1/T
3.3 模拟结果和分析
采用修正的L-J 位错密度模型结合CA方法模拟AZ31镁合金的动态再结晶过程。CA(Cellular Automata)是一种用来描述系统在离散空间—时间上演化规律的数学算法[18]。本文作者将模拟区域划分为150×150网格,每个网格表示2 μm,模拟0.3 mm×0.3 mm的实际样品区域。模拟所用的材料常数如下表1。
图6所示为应变速率为0.03 s-1、真应变为1时不同温度下模拟的微观组织。观察模拟的微观组织,晶粒基本为等轴晶结构,并且随着温度的增加,晶粒尺寸也随之增加。这是由于随着温度的升高,晶界迁移速度增加,同时形核率下降,从而新生晶粒有足够的空间生长,导致晶粒粗化。图7所示为实验的微观组织。由图7可看出,随着温度的增加,晶粒粗化。比较图6和7可知,模拟的结果与实际的微观组织相近,模拟的晶粒尺寸的变化规律与实际相符,证明了修正的 L-J位错密度模型结合 CA可以准确的模拟AZ31镁合金的动态再结晶。

表1 AZ31合金的材料参数Table 1 Materials parameters of AZ31 magnesium alloy
表2所列为模拟的晶粒尺寸和实际的晶粒尺寸的比较。通过表1表明模拟的晶粒尺寸与实际的再结晶粒尺寸误差在8%以内。
图8所示为不同温度下应变速率分别为 0.03和0.3 s-1模拟的流变应力曲线与实验的流变应力曲线。结果表明,模拟曲线与实验曲线存在误差,这是由于在模拟时将初始状态理想化,例如均匀的位错和能量分布以及随机的晶粒取向,忽略材料本身某些位置的位错堆积和能量起伏等情况。但是总体来说,模拟的结果与实验结果一致,进一步证明了修正的 L-J位错密度模型可以用于AZ31镁合金位错密度演变的计算。

图6 应变速率为0.03 s-1和真应变为1时不同温度下的模拟微观组织Fig.6 Simulated microstructures under different temperatures at strain rate of 0.03 s-1 and true strain of 1: (a)300 ℃; (b)400 ℃;(c)500 ℃

图7 应变速率为0.03 s-1和真应变为1时不同温度下的金相组织Fig.7 Optical microstructures under different temperatures at strain rate of 0.03 s-1 and true strain of 1: (a)300 ℃; (b)400 ℃; (c)500 ℃

表2 应变速率为0.03 s-1和真应变为1时不同温度模拟的晶粒尺寸和实验数据的比较Table 2 Comparison of final grain size for simulation with experimental data at strain rate of 0.03 s-1 and true strain of 1
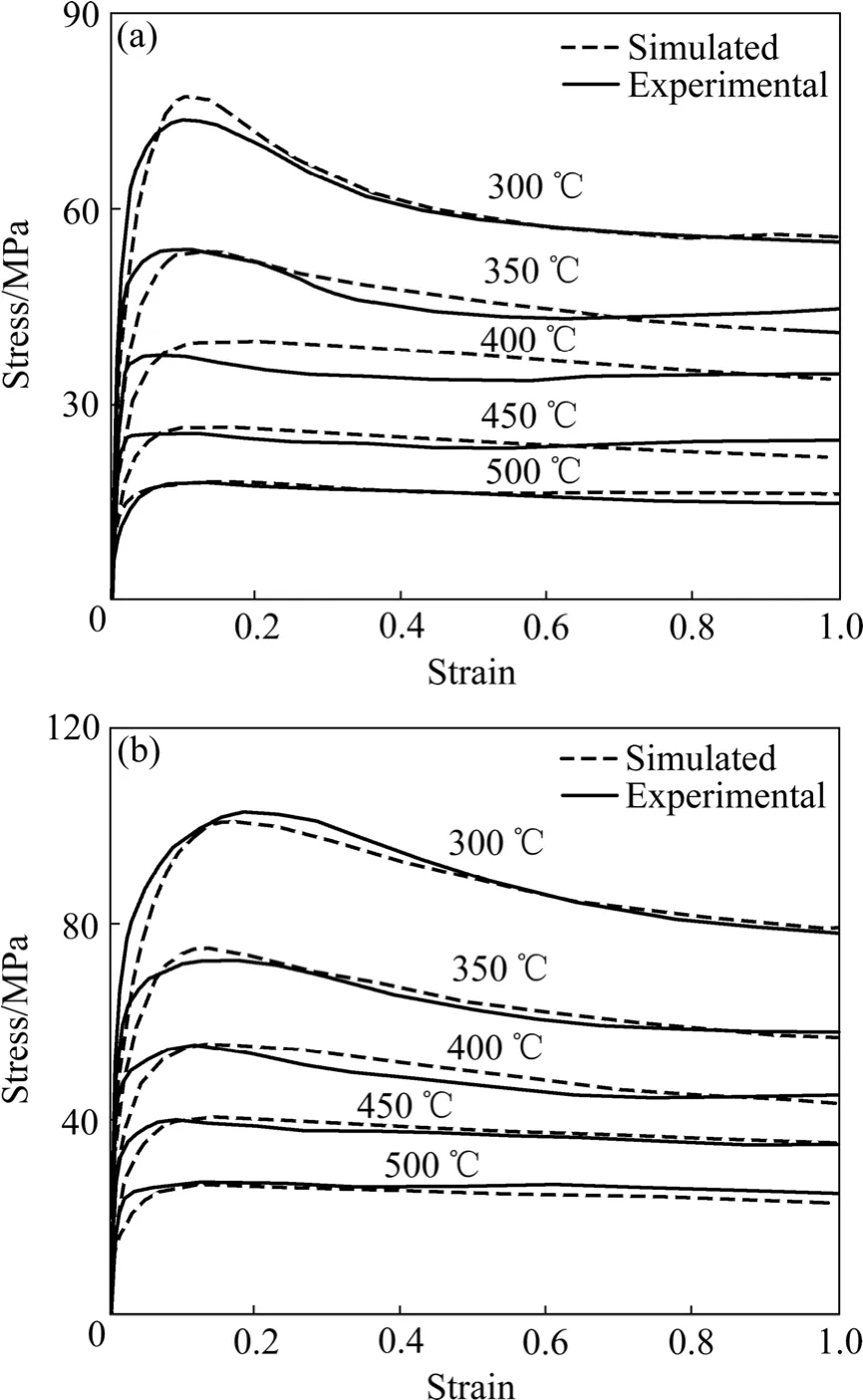
图8 不同温度下模拟的流变应力曲线和实验的流变应力曲线Fig.8 Simulated and experimental curves at different temperatures: (a)0.03 s-1; (b)0.3 s-1
4 结论
1)通过AZ31镁合金流变应力曲线分析和图形变换求解不同应变速率下的回复参数r,其自然对数lnr与温度倒数1/T呈线性相关关系,并且不同应变速率下,lnr—1/T斜率相似,表明可以采用修正的L-J位错密度模型进行动态再结晶过程中的位错密度演变计算。
2)通过采用修正的L-J位错密度模型结合CA可以准确地模拟AZ31镁合金的动态再结晶演变过程。
[1]AGHION E, BRONFIN B.Magnesium alloys development towards the 21st century[J].Materials Science Forum, 2000,350/351: 19-30.
[2]王文先, 张金山, 许并社.镁合金材料的应用及其加工成型技术[J].太原理工大学学报, 2001, 32(6): 599-610.WANG Wen-xian, ZHANG Jin-shan, XU Bing-she.Application and modeling technology for magnesium alloy materials[J].Journal of Taiyuan University of Technology, 2001, 32(6):588-610.
[3]FRIEDRICH H, SCHUMANN S.Research for a “new age of magnesium” in the automotive industry[J].Mater Process Tech,2002, 1l7(3): 276-281.
[4]陈振华, 夏伟军, 程永奇, 傅定发.镁合金织构和各向异性[J].中国有色金属学报, 2005, 15(1): 1-11.CHEN Zhen-hua, XIA Wei-jun, CHEN Yong-qi, FU Ding-fa.Texture and anisotropy in magnesium alloys[J].The Chinese Journal of Nonferrous Metals, 2005, 15(1): 1-11.
[5]陈振华.变形镁合金[M].北京: 化学工业出版社, 2005.CHEN Zhen-hua.Wrought magnesium alloy[M].Beijing:Chemical Industry Press, 2005.
[6]HUMPHREYS F J, HATHERLY M.Recrystallization and related annealing phenomena[M].Oxford: Pergamon, 1995.
[7]DING R, GUO Z X.Coupled quantitative simulation of microstructure evolution and plastic flow during dynamic recrystallization[J].Acta Materialia, 2001, 49: 3163-3175.
[8]CHEN Fei, CUI Zhen-shan, LIU Juan, ZHANG Xiao-xun,CHEN Wen.Modeling and simulation on dynamic recrystallization of 30Cr2Ni4MoV rotor steel using the cellular automaton method[J].Modeling and Simulation in Materials Science and Engineering, 2009, 17: 1-19.
[9]JONAS J J, QUELENNEC X, JIANG L, MATIN É.The Avrami kinetics of dynamic recrystallization[J].Acta Materialia, 2009,57: 2748-2756.
[10]FURRER D U, SEMIATIN S L.A Fundamental of Modeling for Metal Processing[M].New York: ASM Handbook, 2009, 22A.
[11]GOURDET S, MONTHEILLET F.A model of continuous dynamic recrystallization[J].Acta Materialia, 2003, 51:2685-2699.
[12]潘金生, 全健民, 田民波.材料科学基础[M].北京: 清华大学出版社, 2007.PAN Jin-sheng, QUAN Jian-min, TIAN Min-bo.Foundation of materials science[M].Beijing: Tsinghua University Press, 2007.
[13]XIAO Hong, XIE Hong-biao, YAN Yan-hong, JUN Y.Simulation of dynamic recrystallization using automaton method[J].J Iron & Steel Res Int, 2004, 11(2): 42-45.
[14]李落星, 何凤仪, 刘 筱, 周 佳.AM80-0.2Sr-1.5Ca镁合金高温压缩过程的动态再结晶模拟[J].湖南大学学报:自然科学版, 2011, 12: 46-51.LI Luo-xing, HE Feng-yi, LIU Xiao, ZHOU Jia.Simulation of the dynamic recrystallization of AM80-0.2Sr-1.5C magnesium alloy during hot compression deformation[J].Journal of Hunan University: Natural Science, 2011, 12: 46-51.
[15]SAKAI T, JONAS J J.Dynamic recrystallization: Mechanical and microstructural considerations[J].Acta Metall, 1984, 31(2):189-209.
[16]WEISS I, ALVARADO P J, FITZSIMONS G, DEARDO A J.Grain refinement and coarsening during dynamic recrystallization in plain carbon steel[J].Scripta Metallurgica,1983, 17: 693-697.
[17]POLIAK E I, JONAS J J.A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization[J].Acta Metallurgica, 1996, 44(1): 127-136.
[18]何 燕, 张立文, 牛 静, 裴继斌.元胞自动机再结晶过程模拟[J].材料热处理学报, 2005, 26(4): 120-125.HE Yan, ZHANG Li-wen, NIU Jing, PEI Ji-bin.Simulation of dynamic recrystallization process using cellular automata[J].Transactions of Materials and Heating Treatment, 2005, 26(4):120-125.

