模拟退火算法在动力定位能力评估中的应用

刘正锋，刘长德，匡晓峰，周德才

（中国船舶科学研究中心，江苏 无锡214082）

1 引 言

动力定位能力评估是动力定位系统设计中十分重要的环节，动力定位系统都必须进行定位能力分析。动力定位能力分析参考的依据主要有：国际标准《石油和天然气工业海上建筑物的特殊要求》第7部分：《浮动式海上建筑物和移动式海上设备的定位系统》（标准号：ISO19901-7-2005）、美国石油协会（API）的RP 2SK部分《浮式结构定位系统设计和分析的推荐做法》以及国际海事承包商协会（IMCA）的建议《动力定位能力曲线说明书》[1]。设计单位或者厂家依据上述指导意见开发了自己的分析软件和方法。其中，Kongsberg公司开发的软件StatCap在全球享有盛名，计算结果常被设计建造单位用来作为参考标准。CSSRC也根据上述相关指导意见自编了动力定位能力评估软件。

动力定位能力评估的数学描述就是求解带约束的非线性规划问题。常用求解方法有牛顿法、最速下降法、序列二次规划法和信赖域法等。然而，由于动力定位系统通常配备有多推进器，非线性规划问题的解是多元、多局部极值的复杂空间解，即解空间存在无数个局部最优值。传统的算法在寻找全局最优点时，除非初值的选取非常地接近最优点，一般效率都非常的低。同时，求得的最优点很可能是局部最优点，而很难确定结果的正确性。模拟退火算法处理这一类非线性规划问题较为成功[2-3]。模拟退火算法源于对固体退火过程的模拟。采用Metropolis接受准则，并用一组称为冷却进度表的参数来控制算法进程，使得算法在多项式时间里给出一个近似最优解。固体退火过程的物理现象和统计性质是模拟退火算法的物理背景。Metropolis接受准则使算法能够跳离局部最优的“陷阱”，是模拟退火算法能够获得整体最优解的关键；而冷却进度表的合理选择是算法应用的关键。

本文将主要介绍模拟退火算法在动力定位能力分析中的应用,对实例进行了控位能力计算，并将计算结果与Kongsberg的计算结果进行比较分析。

2 动力定位能力评估模型

动力定位系统主要通过控制推进器发出的推力来抵消外界环境外力的影响，仅考虑水平面的运动控制，即纵荡、横荡以及艏摇的控制，如图1所示。

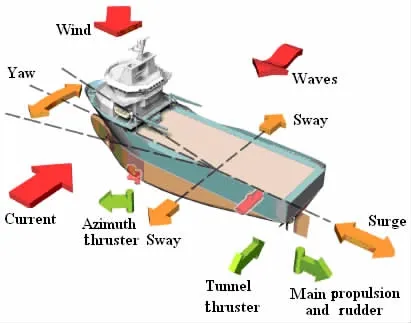
图1 动力定位示意图[4]Fig.1 Sketch map of dynamic positioning

动力定位能力分析的目的就是计算船舶所能承受的各方向上最大的风速，即最恶劣的海况，因此风、浪、流被假定为同向的，载荷可以相互叠加。风、浪、流等外界环境载荷可以通过数值计算或者试验方法获得，结合推进器的位置布局及性能参数，可以建立动力定位能力分析数学模型如下：

目标函数f：

约束条件：

推进器性能约束：

Vw表示风速。方程（1）中，ρi表示第i个推进器的状态，ρi=1表示该推进器工作，ρi=0表示该推进器不工作，0＜ρi＜1表示该推进器工作，但是推力有损失。Ti为第i个推进器推力，θi为该推力角度，（xi，yi）分别表示第i个推进器在选定坐标系中的位置。F、N分别表示外界力和力矩。下标x，y分别表示纵向和横向，下标w，c，wa，a分别表示风，流，波浪以及附加外力。方程（2）表示推进器的约束条件，Di表示推进器可执行的角度区域。

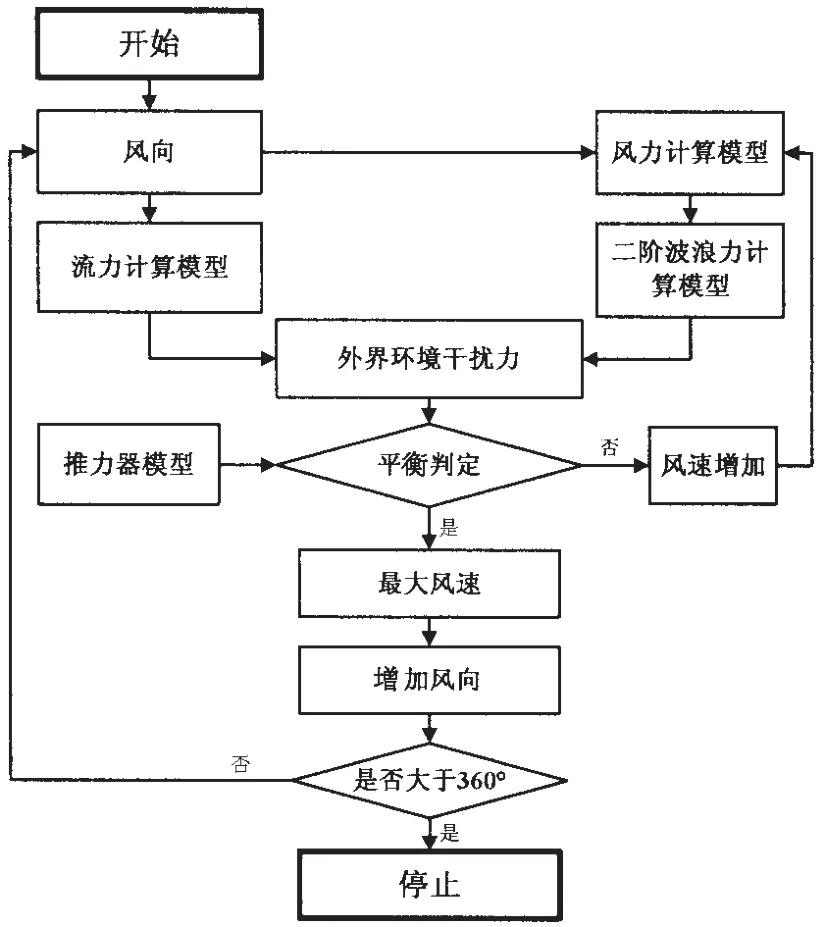
图2 动力定位能力评估程序流程图Fig.2 DP capability analysis flow chart

通常，海流速度假设是已知的，波浪是由风生成的。波浪和风之间的关系可以参考海区和相关资料决定。结合方程（1～2），可以对各工作模式下的动力定位能力进行评估。在海流已知的条件下，从迎面来风（0°角）开始，求得该风向下，动力定位船舶所能承受的最大风速以及此时的各推进器的推力分配；该风向计算完成时，风向角增加特定角度并进行该方向最大风速的求解，一直增加至360°完成整个周向计算。根据不同风向所得的最大风速，可以画出该动力定位船舶的控位能力玫瑰图。计算流程如图2所示。

各方向最大风速的求解就是一个非线性约束优化问题，可以采用模拟退火算法进行计算。下面将对模拟退火算法进行介绍。

3 模拟退火算法

模拟退火算法是基于Monte Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。SAA在某一温度下，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。具体步骤如下：

模拟退火算法用Metropolis算法产生组合优化问题解的序列，并由与Metropolis准则对应的转移概率P：

设tk=T（tk-1）表示Metropolis算法第k次迭代时控制参数t的值，T（t）表示控制参数更新函数，tf表示终止温度。Lk表示Metropolis算法第k次迭代时产生的变换个数。下面以最小化目标函数f（x）为例，给出模拟退火算法的具体操作步骤：

（1）设置初始温度t0、终止温度tf及控制参数更新函数T（t）；

（2）随机产生初始解x0，以此作为当前最优点xopt=x0，计算目标函数值f（xopt）；

（3）对当前最优点作一随机变动，产生一新解xk，计算新解的目标函数值f（x），并计算目标函数值增量 △f=f（x）-f（xopt）；

（4）若△＜0，则接受该新解为当前最优点，xopt=x；若△≥0，则以概率p的方式接受该新解为当前最优点；

（5）若k＜Lk，则k←k+1，转（4）；tk=T（tk-1）。设置Lk，令循环计数器初值k＝0；

（6）若t≥Tf，则转（3）；若t＜Tf，则输出当前最优点，算法结束。

模拟退火算法具有渐近收敛性，在理论上已被证明以概率1收敛于全局最优解，其具体操作流程如图3所示。

模拟退火算法依据Metropolis准则接受新解，因此除接受优化解外，还在一个限定范围内接受恶化解，这正是模拟退火算法与其他局部搜索算法的本质区别所在。开始时t值大，可能接受较差的恶化解；随着t值的减少，只能接受较好的恶化解；最后在t值趋于零时，就不再接受任何恶化解了。这就使模拟退火算法既可以从局部最优的“陷阱”中跳出，更能求得组合优化问题的整体最优解。模拟退火算法通用性强，对问题信息依赖较少，因此在诸多工程和学术领域中得到了研究和应用。

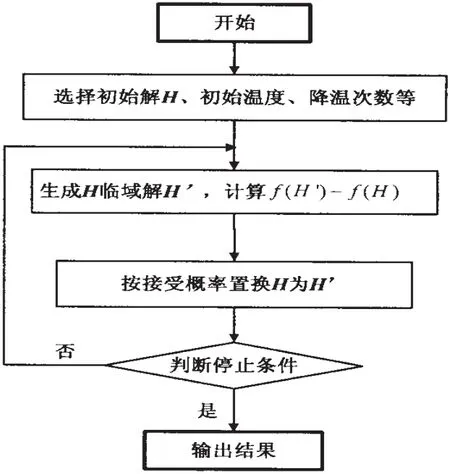
图3 模拟退火算法操作流程图Fig.3 Flow chart of simulated annealing algorithm

4 算例验证

下面我们将通过具体算例对模拟退火算法在动力定位能力评估的应用进行检验，验证其有效性。槽道推进器（Tunnel）和全回转推进器（Azimuth）是动力定位船舶中最经常用到的推进器，本文将采用如下两个算例进行计算，并与Kongsberg的结果进行比较。

4.1 Adams Arrow工程船[5]

Adams Arrow工程船上的推进器布局如图4所示。

图4 Adams Arrow推进器布局图Fig.4 Thruster layout on Adams Arrow

风、浪和流载荷根据Kongsberg报告中相关系数曲线进行预报，下面对完整工作模式以及局部推进器失效模式下的动力定位能力进行计算，结果如图5-8所示。

表1 推进器布局及性能指标Tab.1 Thruster layout and parameters

从图5-8的对比中可以看出，利用模拟退火算法计算的动力定位能力和Kongsberg计算结果符合得相当好。在90°和270°风向角附近，计算结果扰动的原因是对这些方向的风力系数、二阶波浪力系数插值引入的误差而导致的。可见，模拟退火算法在控位能力分析中的应用整体上是成功的、可靠的。

为了进一步给出该方法计算结果与Kongsberg的区别，我们将利用下个算例仔细分析两种评估方法对力以及力矩平衡约束的满足程度。

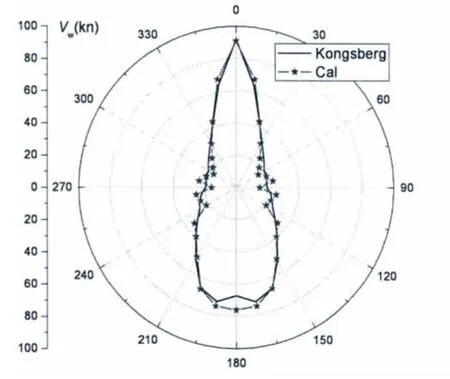
图5 所有推进器均正常工作（Adams Arrow）Fig.5 Intact mode

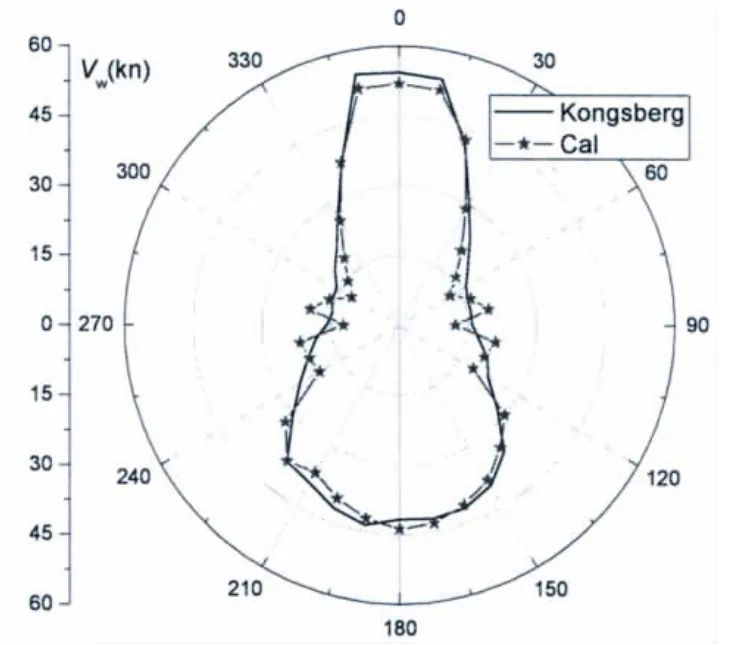
图6 推进器2不工作（Adams Arrow）Fig.6 Thruster 2 failure

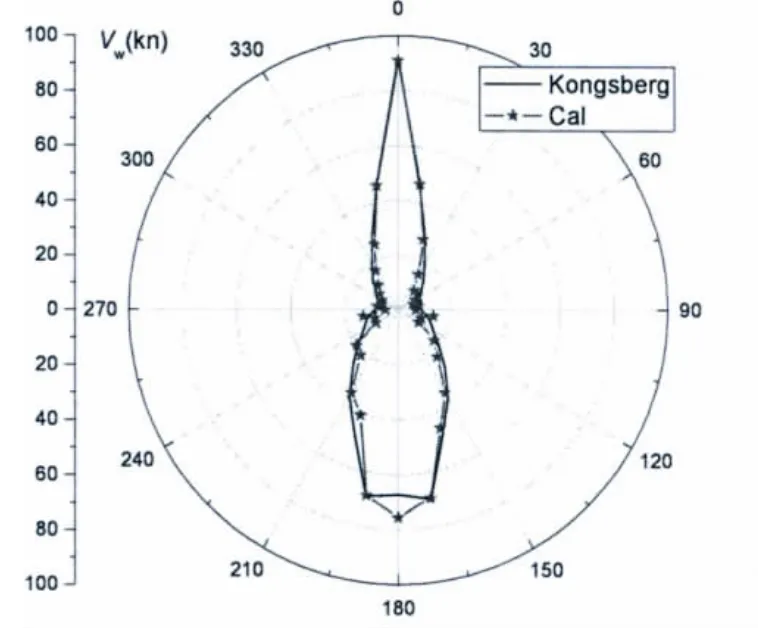
图7 推进器4不工作（Adams Arrow）Fig.7 Thruster 4 failure

图8 推进器2、3不工作（Adams Arrow）Fig.8 Thrusters 2 and 3 failure

4.2 CNOOC DPV 7500C铺管船[6]

CNOOC DPV 7500C铺管船上各推进器的位置布局如图9所示。

图9 CNOOC DPV 7500C推进器布局示意图Fig.9 Thruster layout on CNOOC DPV 7500C

各推进器的位置及性能指标如表2所示。

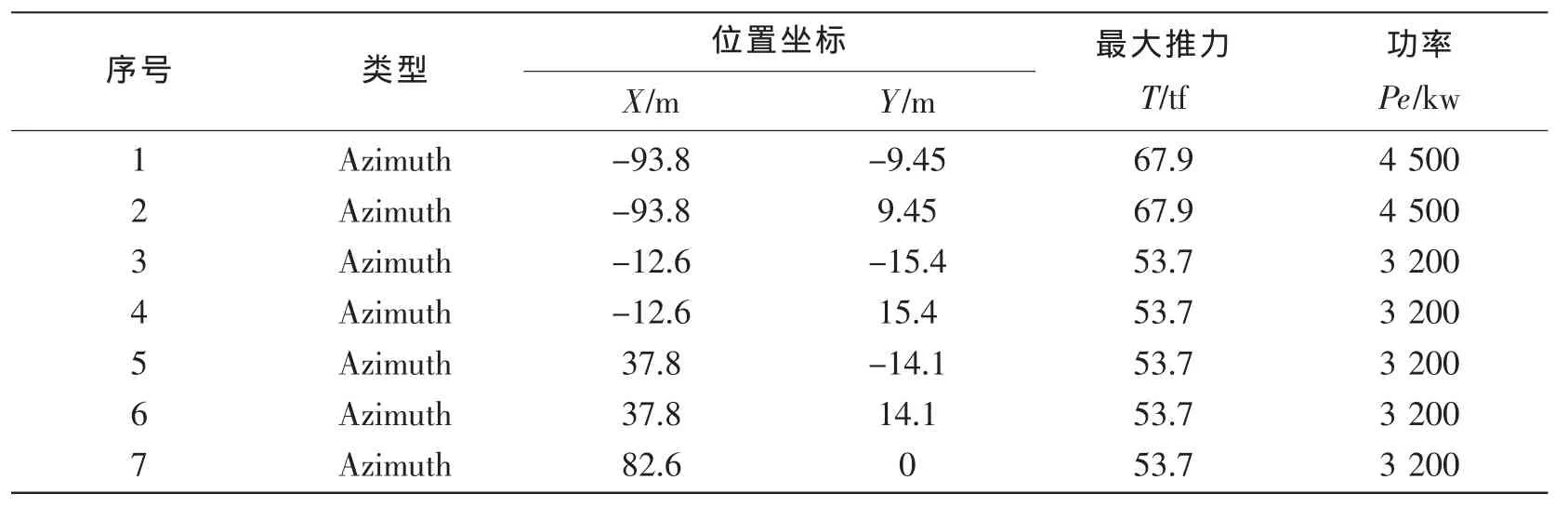
表2 推进器位置布局及性能指标Tab.2 Thruster layout and parameters

风、浪和流载荷根据Kongsberg报告中相关曲线进行预报，对完整工作模式以及局部推进器失效模式下的动力定位能力进行计算，结果如图10-11所示。各方向的合力（合力矩）相对误差如表3-4所示。

从图10和图11的对比中可以看出，计算结果与Kongsberg提供的结果吻合得相当好。在60°和300°附近，该船所能承受的极限风速最小，即在该方向上控位能力最差。在0°风向，即顶风时，该船的控位能力最强。

图10 完整工作模式（CNOOC DPV 7500C）Fig.10 Intact mode(CNOOC DPV 7500C)

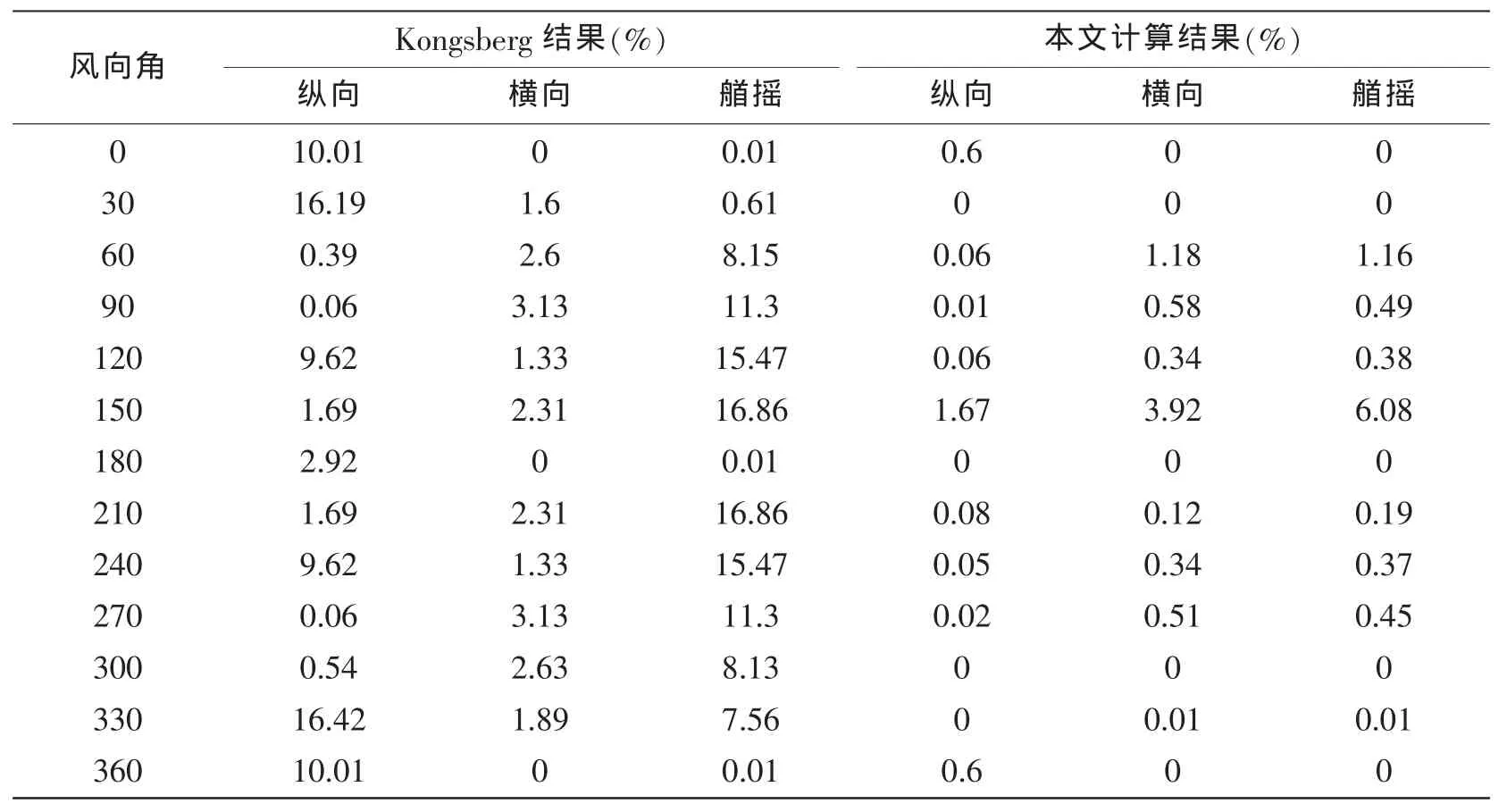
表3 各方向合力相对误差（Intact mode）Tab.3 Relative error of surge,sway and yaw direction(Intact mode)

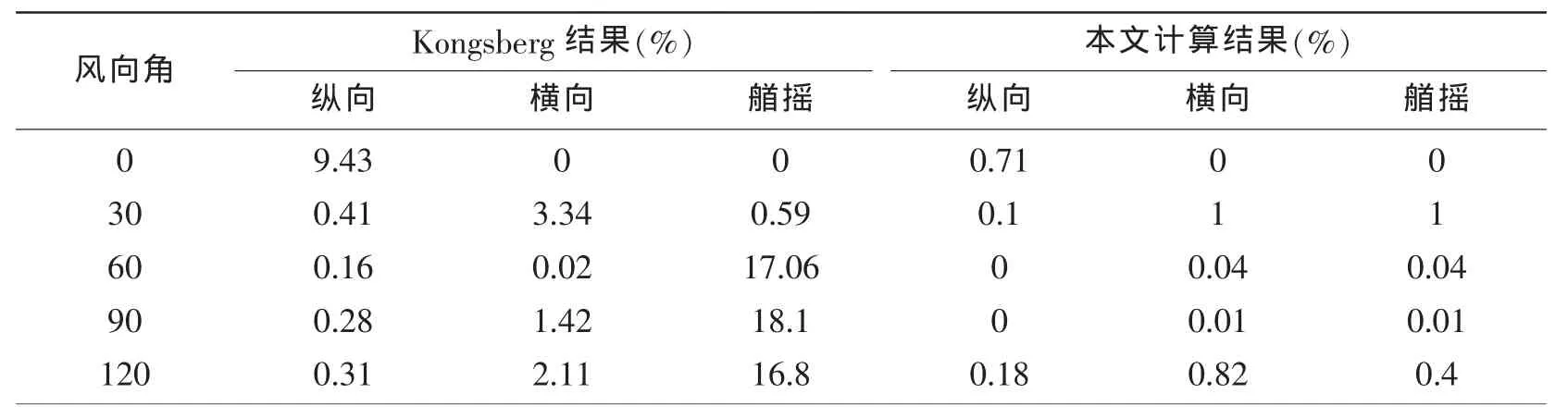
表4 各方向合力相对误差（No.7 thruster failure）Tab.4 Relative error of surge,sway and yaw direction(No.7 thruster failure)

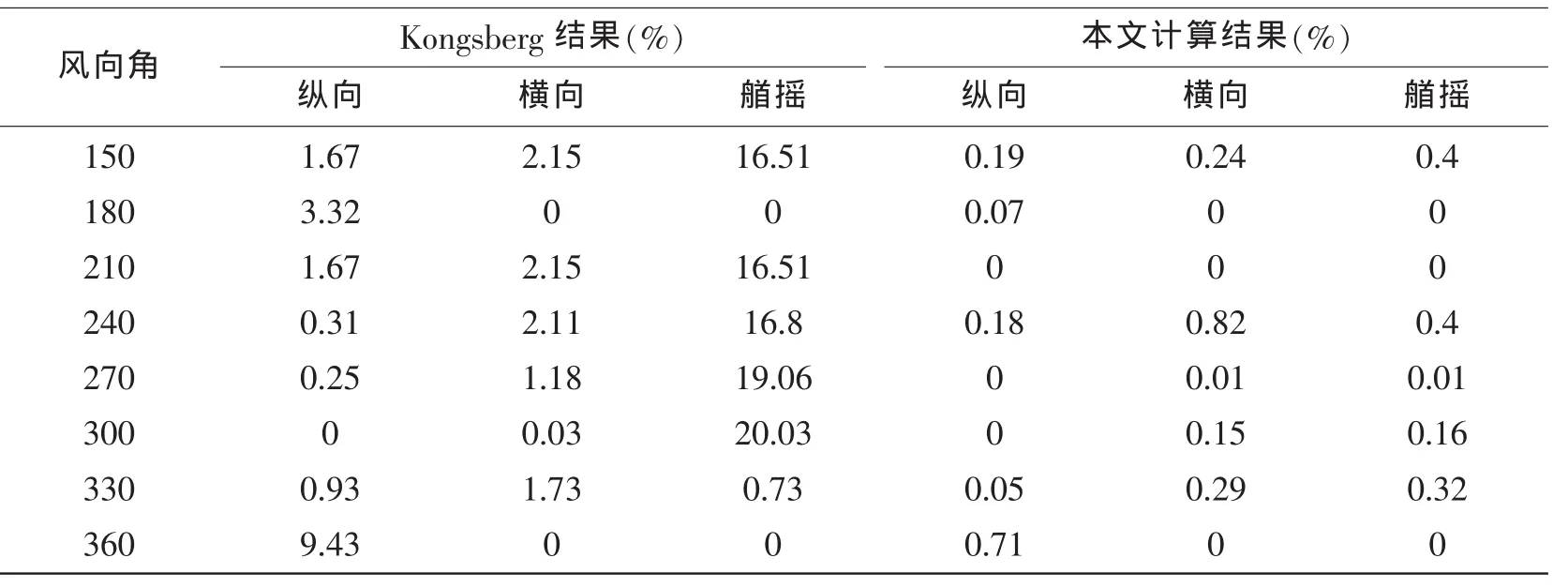
续表4

从表3和4中可以看出，在动力定位能力评估时，Kongsberg对三方向上合力及力矩的约束不严格，尤其对力矩的约束，在某些角度达到20%左右；而本文利用模拟退火算法求解时，误差基本控制在1%以内，严格地满足了力的平衡和力矩的平衡条件。

5 结 论

动力定位能力评估的数学描述是典型的非线性约束优化问题，模拟退火算法是解决这类问题比较成功的方法。本文对模拟退火算法在动力定位能力评估的应用进行了尝试，并对实例进行了计算。算例分析结果与Kongsberg结果对比表明，基于模拟退火算法开发的动力定位能力评估方法是可靠、成功的。它可以更为严格地满足动力定位能力分析所要求的力与力矩平衡等约束条件。

动力定位技术研究在国内也已经开展了相当长一段时间，然而国内研究者对动力定位能力的评估所做的工作并不多见，本文在这方面做出了有益的尝试。本文工作对于分析船舶的控位能力及选择船舶的推进器配置具有一定的参考价值，同时也为进一步深入研究该领域打下了基础。

[1]张本伟,杨鸿等.动力定位控位能力分析方法探讨[J].中国造船,2009,50 special:205-214.Zhang Benwei,Yang Hong,et al.Investigation on the methods used in the analysis of DP capability[J].Shipbuilding of China,2009,50 special:205-214.

[2]张长林,余建星,等.非线性约束最优化问题的多目标模拟退火算法[J].复旦学报,2003,42(1):93-97.Zhang Changlin,Yu Jianxing,et al.The multi-object simulated annealing algorithm for the nonlinear constraint optimization problem[J].Journal of FuDan University,2003,42(1):93-97.

[3]王正林,等.精通MATLAB科学计算[M]．北京:电子工业出版社,2008.Wang Zhenglin,et al.Proficiency in MATLAB scientific computing[M].Beijing:Publishing House of Electronic Industry,2008.

[4]Mahfouz A B,El-Tahan H W.On the use of the capability polar plots program for dynamic positioning systems for marine vessels[J].Ocean Engineering,2006,33:1070-1089.

[5]DP capability analysis:Adams Arrow[R].Kongsberg Maritime AS,2008.

[6]DP capability analysis:DP class 3 crane operation CNOOC DPV 7500C[R].Kongsberg Maritime AS,2009.