盾构导向系统控制点布设优化分析
宫玮清
(1. 同济大学测绘与地理信息学院,上海 200092;2. 上海隧道工程股份有限公司,上海 200062)
在城市地铁建设中,盾构法施工有其独特优势,成为城市隧道施工的首选工法。而在软土层中进行盾构法施工,为防治地面沉降等环境地质问题[1~3],实时监测是必不可少的[4~7]。在施工中对盾构姿态的控制是关键工序,及时测量盾构机的姿态,可使盾构掘进线路与设计轴线之间的误差控制在一定范围内。盾构姿态的测量方法一般分为激光法、棱镜法、陀螺仪定向三大类,相比较而言,棱镜法在测量精度、设备成本、操作难易程度等方面具有优势,故应用较为普遍。
棱镜法是采用坐标转换来解算盾构姿态,属于间接测量的方法。而棱镜布设位置与最终的解算精度有很大关系,因此对棱镜的布设位置进行研究有利于提高解算精度,从而为盾构姿态的控制提供保障。
本文对采用坐标转换方法的盾构导向系统解算过程进行分析,并根据误差理论探讨棱镜控制点的优化布设原则与实施方案。
1 盾构姿态的棱镜法解算原理与方法
在隧道施工前,先测定盾构机的初始姿态,同时在盾构机上安装3个以上棱镜,测量它们的坐标,此坐标在施工坐标系O-XYZ下;同时建立盾构坐标系o-xyz,并得到各个棱镜在盾构坐标系中的坐标,这些棱镜就作为施工坐标系O-XYZ与盾构坐标系o-xyz之间的公共点。这些点在盾构整个掘进过程中,棱镜和盾构机的相对关系是固定的。
在盾构机掘进过程中,盾构机的姿态发生变动,相当于盾构坐标系发生了平移和旋转,此时施工坐标系O-XYZ与盾构坐标系o-xyz之间的旋转参数由已知变为未知。此时再次测量棱镜坐标,利用空间三维坐标旋转运算,用最小二乘法拟合,求得6个旋转参数,重新得到盾构姿态[8~11]。
坐标旋转公式:

式中:

由于有6个待求值,所以至少需要3个棱镜坐标。
实测盾构机各棱镜,得到新的绝对坐标,并以此分别列出误差方程:

各旋转阵:


以间接平差方式求解,由于是同精度观测,所以权阵P取单位阵,得到δx,未知数由近似值x0修正为x0+δx;重新组成误差方程、法方程,求解δx、修正近似值,迭代至改正数δx足够小(收敛),最终得到旋转参数。
验后单位权中误差σ0:

在平差前,将旋转参数的初值代入得到系数阵A0,并给定验前单位权中误差,则可对旋转参数的求解精度进行验前估计。D为方差—协方差阵,旋转参数的求解精度为:

对任意转换点,将其坐标代入式(4),得到矩阵Ai,L为任意观测值,由误差传播定理[12],坐标转换后其精度为:

2 控制点布设及其优化
棱镜法是通过测量盾构机内部的棱镜坐标,采用坐标转换来解算盾构姿态,属间接测量,所以影响系统精度的因素比较多。它不仅与棱镜坐标本身的测量误差有关,还与由此产生的误差在计算中的传递有关。在相同的测量精度下,比较好的网型可以很好地控制误差的传播。因此,棱镜布点及其优化对于提高系统自身的解算精度是一关键环节。
在盾构机内部布置3个点,其无论怎样布置,都可分解为在XOY与XOZ上的投影。在XOY面上时,如控制点布设在同一水平面(盾构坐标Z方向坐标值相等),则此3点的投影图形,其投影的三角形的一条边或垂直于X轴,或相交于X轴。
假设棱镜的观测误差为1mm,利用协因数阵对不同的布点方案进行讨论。
2.1 布设方案
选择6种布设方案作比较分析,其控制点布置网型见图1、其盾构坐标见表1。

图1 控制点布设方案Fig.1 The disposal scheme of control point

表1 布设方案的控制点盾构坐标 (m)Table 1 The shield coordinates of control points of disposal scheme
2.2 精度分析
为评估布设方案的精度,并遴选出优化原则,对不同网型的参数求解精度进行比较分析。
布设方案(a)是假设控制点布设在同一水平面(盾构坐标Z方向坐标值相等),为各点在盾构坐标系中的分布,固定1#点,分别取(1#,2#,3#)、(1#,4#,5#)、(1#,6#,7#)、(1#,6#,8#)构成不同的网型。
方案(b)、方案(c)都是在方案(a)基础上,分别考虑第3个点在沿Y轴、X轴布设的情况。均固定1#,2#点,分别取(1#,2#,3#)、(1#,2#,4#)、(1#,2#,5#)构成不同的网型。
a,b,c三种方案均属控制点投影三角形的一条边垂直于X轴的情况,而方案d,e,f则为控制点投影三角形的一条边与X轴相交情况。
方案(d)是取第三个点布设在X轴附近,固定1#,2#点,分别取(1#,2#,3#)、(1#,2#,4#)、(1#,2#,5#)构成不同网型。
方案(e)、方案(f)都是在方案(d)基础上,将三个控制点在平面上的布设定为前二后一的形式,并且前两个控制点垂直于X轴,后一个控制点在X轴附近,再将控制点投影到XOZ面上,讨论控制点沿Z轴布置对解算精度的影响。
其中方案(e)是固定前两个点的高度,考虑后一个点的高差情况;方案(f)是固定后一个点和前一个点的高度,考虑另一个点的高差情况。同样固定1#,2#点,分别取(1#,2#,3#)、(1#,2#,4#)、(1#,2#,5#)构成不同的网型。
6种布设方案的参数求解精度见表2。
2.3 结果评价
由表2可以看出,对于布设方案(a)而言,若沿Y轴布设两个控制点,其布设的间隔越大,其解算精度越高,对各解算参数的精度都有提高,对Y坐标与α的解算精度提升明显,而且,最好能分布在轴线两侧。
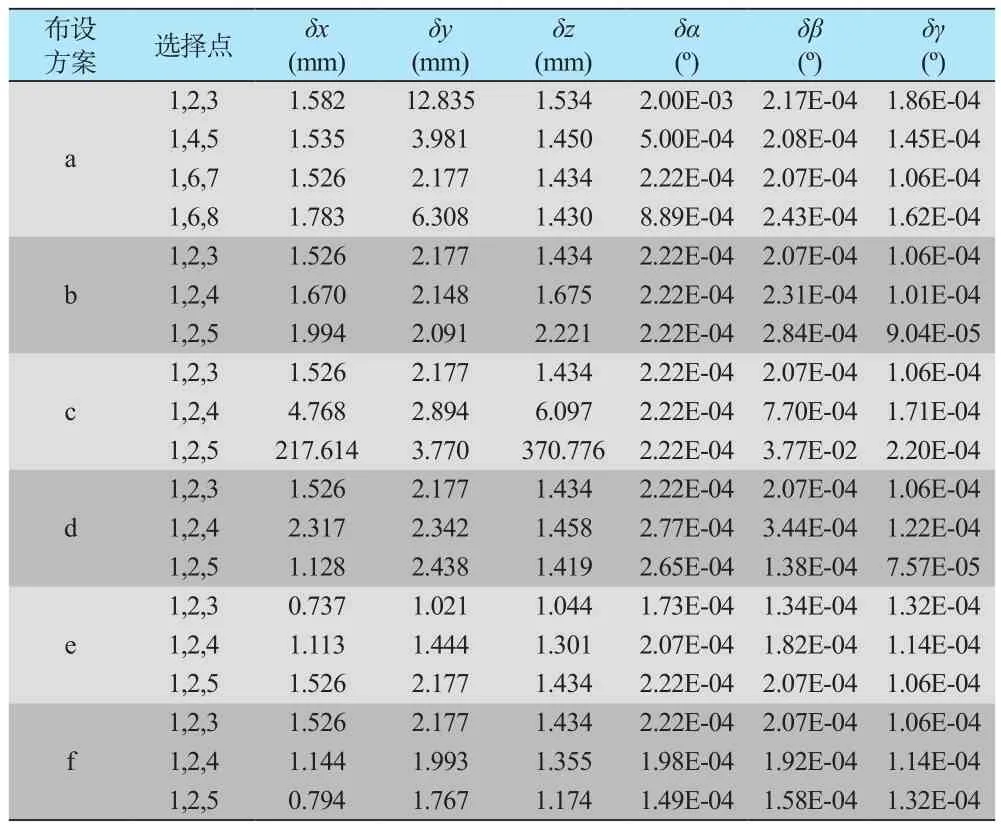
表2 布设方案参数求解精度Table 2 The parameter accuracy of disposal scheme
方案(b),控制点布置在中轴线附近,虽然Y坐标和γ的精度略有降低,但其他参数解算精度都有提高,而且相比较而言,参数解算精度比较均衡。
方案(c),沿X轴布置的控制点,其布设的间隔越大,其解算精度越高,对X坐标、Z坐标和β的解算精度提升尤为明显。
方案(d),此形式布设的控制点对解算精度的提高并不明显;而方案(e)、方案(f)表明,相互间的高差越大,其6个参数的解算精度越高,但是γ的精度相反。
综上分析,控制点在水平面上布设时,沿Y方向的控制点,对Y坐标与α的解算精度有较大影响,控制点的间距越大,Y坐标与α的解算精度提升越明显;沿X方向的控制点,对X坐标、Z坐标和β的解算精度有较大影响,间距越大,对其精度的提升越显著;沿Z方向的控制点,对6个参数的解算都有一定影响,各控制点间Z方向的间距越大,总体解算精度就越高,只有γ的精度会降低。
3 结论
本文基于空间三维坐标旋转,对盾构姿态解算方法与精度进行了分析,特别是对棱镜的布设及其优化作了探讨。布置在盾构机内部的棱镜作为解算的控制点,它的布设形式对解算的精度有直接的影响,盾构机内部的空间有限,布点很难达到良好的网型结构,但在有限的空间内,可以尽量将网型布设得较为合理,以提高解算精度。棱镜布设的要点就是三个棱镜之间的间距尽可能拉大,并均匀布置在盾构中轴线两侧,并使它们之间有相应的高差。
References)
[1]胡坚,王军. 盾构法隧道的纵向沉降问题[J]. 上海地质,2000, 21(3):13-18.
Hu J, Wang J. Longitudinal settlement of shield tunnel[J].Shanghai Geology,2000,21(3):13-18.
[2]璩继立,峁会勇. 盾构施工地面长期沉降的神经网络预测[J]. 上海地质,2004,25(3):42-46.
Qu J L, Mao H Y. Artif i cial neural network prediction of surface long-term settlement induced by shield construction [J]. Shanghai Geology,2004,25(3):42-46.
[3]杨天亮,严学新,王寒梅,等. 地铁隧道盾构施工引起的工程性地面沉降研究[J]. 上海地质,2010,31(S1):7-11.
Yang T L, Yan X X, Wang H M, et al. Study on engineering land subsidence caused by shield construction in subway tunnel[J].Shanghai Geology,2010,31(S1): 7-11.
[4]司永峰. 基于姿态测量的深埋小口径地下管道探测技术研究[J].上海地质,2009,30(4):21-24,28.
Si Y F. Study on technology of detecting deep underground pipelines with small diameter based on the attitude measurement[J].Shanghai Geology,2009,30(4):21-24,28.
[5]张金华. 双层隧道变形的收敛测量方法与实例分析[J]. 上海国土资源,2012,33(1):87-90.
Zhang J H. Ιntroduction and analysis of technical method to measure convergence in double deck tunnel[J]. Shanghai Land &Resources,2012,33(1):87-90.
[6]庄一兵,詹龙喜,许准,等. 基于光纤光栅技术的地铁隧道沉降监测[J]. 上海国土资源,2012,33(3):76-78.
Zhuang Y B, Zhan L X, Xu Z, et al. Subsidence monitoring of subway tunnel based on fi ber bragg grating technique[J]. Shanghai Land & Resources,2012,33(3):76-78.
[7]姜晨光,刘冠林,王纪明,等. 基于物联网的隧道智能监测系统设计[J]. 上海国土资源,2013,34(1):85-89.
Jiang C G, Liu G L, Wang J M, et al. Ιntelligent tunnel monitoring system based on a wireless sensor network and the internet of things[J]. Shanghai Land & Resources,2013,34(1):85-89.
[8]王解先,季凯敏. 工业测量拟合[M]. 北京:测绘出版社,2008.
Wang J X. Ji K M. Ιndustrial surveying fitting[M]. Beijing:Surveying and Mapping Press, 2008.
[9]陈义,沈云中,刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报(信息科学版),2004,29(12):1101-1105.
Chen Y, Shen Y Z, Liu D J. A simplif i ed model of three dimensional datum transformation adapted to big rotation angle[J]. Geometrics and Information Science of Wuhan University, 2004,29(12):1101-1105.
[10]李金岭,刘鹂,乔书波,等. 关于三维直角坐标七参数转换模型求解的讨论[J]. 测绘科学,2010,35(4):76-78.
Li J L, Liu L, Qiao S B, et al. Discussion on the determination of transformation parameters of 3D cartesian coordinates[J]. Science of Surveying and Mapping,2010,35(4):76-78.
[11]张厚美,古力. 盾构机姿态参数的测量及计算方法研究[J]. 现代隧道技术, 2004,41(2):14-20.
Zhang H M, Gu L. On the measurement and the method of computation of the posture parameters of shields[J]. Modern Tunneling Technology,2004,41(2):14-20.
[12]武汉测绘科技大学. 测量平差基础(第3版)[M]. 北京:测绘出版社,1996.
Wuhan University of Surveying and Mapping. Basis of surveying adjustment (the third edition)[M]. Beijing: Surveying and Mapping Press, 1996.

